LeetCode 723. Candy Crush
原题链接在这里:https://leetcode.com/problems/candy-crush/
题目:
This question is about implementing a basic elimination algorithm for Candy Crush.
Given a 2D integer array board representing the grid of candy, different positive integers board[i][j] represent different types of candies. A value of board[i][j] = 0 represents that the cell at position (i, j) is empty. The given board represents the state of the game following the player's move. Now, you need to restore the board to a stable state by crushing candies according to the following rules:
- If three or more candies of the same type are adjacent vertically or horizontally, "crush" them all at the same time - these positions become empty.
- After crushing all candies simultaneously, if an empty space on the board has candies on top of itself, then these candies will drop until they hit a candy or bottom at the same time. (No new candies will drop outside the top boundary.)
- After the above steps, there may exist more candies that can be crushed. If so, you need to repeat the above steps.
- If there does not exist more candies that can be crushed (ie. the board is stable), then return the current board.
You need to perform the above rules until the board becomes stable, then return the current board.
Example:
Input: board = [[110,5,112,113,114],[210,211,5,213,214],[310,311,3,313,314],[410,411,412,5,414],[5,1,512,3,3],[610,4,1,613,614],[710,1,2,713,714],[810,1,2,1,1],[1,1,2,2,2],[4,1,4,4,1014]] Output: [[0,0,0,0,0],[0,0,0,0,0],[0,0,0,0,0],[110,0,0,0,114],[210,0,0,0,214],[310,0,0,113,314],[410,0,0,213,414],[610,211,112,313,614],[710,311,412,613,714],[810,411,512,713,1014]] Explanation:
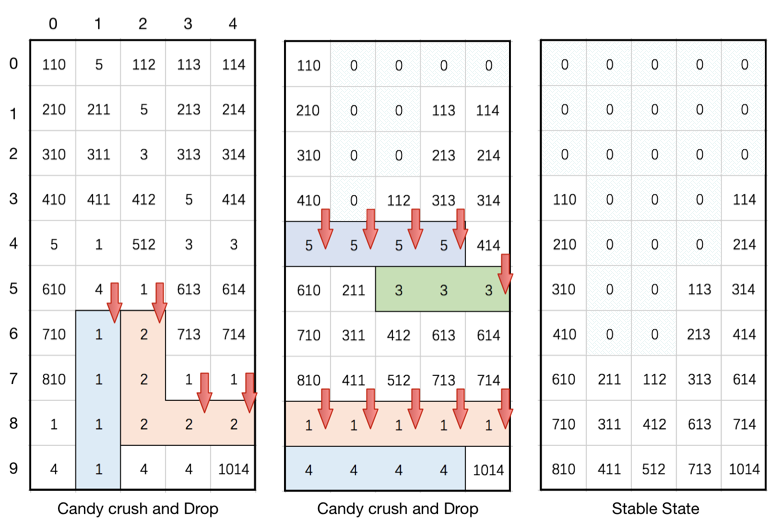
Note:
- The length of
boardwill be in the range [3, 50]. - The length of
board[i]will be in the range [3, 50]. - Each
board[i][j]will initially start as an integer in the range [1, 2000].
题解:
There are two steps.
Step 1: Mark 3 adjacent candies. Check if there are 3 adjacent candies. First check row by row, then column by column.
If there are, mark these values as negative.
Step 2: Crush them. Rewrite board with only positive numbers.
If there is crushing, that means there may be another round of crash, use recursion. Otherwise, there wouldn't be another round of crash, return the board.
Time Comlexity: O(M^2*n^2). m = board.length. n = board[0].length.
Each crash, there would be 3 crashed at minimum. Totally there are m*n candies. So recursion could run for m*n/3 times.
Each recursion, it takes O(m*n).
Space: O(1).
AC Java:
1 class Solution { 2 public int[][] candyCrush(int[][] board) { 3 if(board == null || board.length == 0 | board[0].length == 0){ 4 return board; 5 } 6 7 boolean todo = false; 8 int m = board.length; 9 int n = board[0].length; 10 for(int i = 0; i<m; i++){ 11 for(int j = 0; j<n-2; j++){ 12 int val = Math.abs(board[i][j]); 13 if(val!=0 && val==Math.abs(board[i][j+1]) && val==Math.abs(board[i][j+2])){ 14 todo = true; 15 board[i][j] = board[i][j+1] = board[i][j+2] = -val; 16 } 17 } 18 } 19 20 for(int j = 0; j<n; j++){ 21 for(int i = 0; i<m-2; i++){ 22 int val = Math.abs(board[i][j]); 23 if(val!=0 && val==Math.abs(board[i+1][j]) && val==Math.abs(board[i+2][j])){ 24 todo = true; 25 board[i][j] = board[i+1][j] = board[i+2][j] = -val; 26 } 27 } 28 } 29 30 for(int j = 0; j<n; j++){ 31 int br = m-1; 32 for(int i = m-1; i>=0; i--){ 33 if(board[i][j] > 0){ 34 board[br--][j] = board[i][j]; 35 } 36 } 37 38 while(br>=0){ 39 board[br--][j] = 0; 40 } 41 } 42 43 return todo ? candyCrush(board) : board; 44 } 45 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号