分层图

分层图：

　　将原图分为许多层，通过层与层之间的关系来转移。

应用：

　　一般会和最短路一起考查，题目中会对最短路做一些限制条件，有些就可以通过建分层图来跑最短路。

 

例题引入：

　　飞行路线：https://www.lydsy.com/JudgeOnline/problem.php?id=2763

　　　　　　　 https://www.luogu.org/problemnew/show/P4568

 

　　 Alice和Bob现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在n个城市设有业务，设这些城市分别标记为0到n-1，一共有m种航线，每种航线连接两个城市，并且航线有一定的价格。Alice和Bob现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多k种航线上搭乘飞机。那么Alice和Bob这次出行最少花费多少？

 

例题解答：

　　题目中本意是求最短路，但因为加了可以将最多K条边的费用变为0，所以不可以直接跑最短路，又因为k很小，所以可以用分层图+最短路解决此题了。

　   用dis[u][x]表示到第v个城市已经用了x次免费机会后的最短距离，对于u的下一个城市v，此时到达v的最短距离有两种可能：

　　 1.dis[v][x]=dis[u][x]+p[i].val（u->v这条边不免费）

　　 2.dis[v][x+1]=dis[u][x](u->v这条边免费)

　　用优先队列优化的Dijkstra一直这样做完就可以了，最后的答案是min{dis[t][i]},0<=i<=k。

 

　　还有一种建虚拟节点建边的方式可以实现分层图，也就是将u的下一个城市分为k+1（包括k==0）种状态连边，每一层中点与点之间的边的val同原图，但层与层间的边val为0

　　然后就变成了各自层内不免费但层与层内免费的状态了，再跑最短路即可。

　　下图是样例的建边图示，蓝色的边和绿色的边val不变，黑色的边val=0,5-9为新建的虚拟节点，绿色和黑色的边是新建的虚拟边。

　　图片来自：https://www.luogu.org/blog/ACdreamer/solution-p4568

 

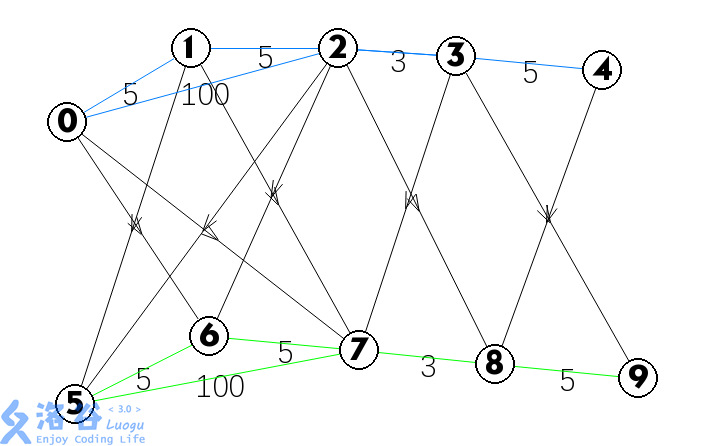
　　通过实测证明后一种虽然比较容易实现，但是在时间和空间上都没有前者优。

　　下图第二个是第一种解法，第一个是第二种解法。

代码实现：

　　

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
#define INF 0x3f3f3f3f
#define maxn 10009
#define maxm 50009
inline ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ll)(ch-'0');ch=getchar();}
    return x*f;
}
int head[maxn];
struct edge
{
    int to,nxt;
    ll val;
}p[maxm<<1]; 
bool vis[maxn][19];
struct node
{
    int id,cnt;//id为城市编号，cnt为已经用的免费次数 
    ll dist;
    bool operator < (const node &temp) const//重载小于运算符，因为优先队列默认为大根堆 
    {
        return dist>temp.dist;
    }
}city[maxm<<1][19];
int n,m,k,tot,s,t,cnt;
ll ans;
void add(int x,int y,ll z)
{
    ++cnt,p[cnt].to=y,p[cnt].val=z,p[cnt].nxt=head[x],head[x]=cnt;
}

void Dijkstra()
{
    priority_queue<node>q;
    memset(vis,0,sizeof(vis));
    for(int i=0;i<=n;i++)
        for(int j=0;j<=k;j++)
            city[i][j].dist=INF;
    city[s][0]={s,0,0};
    q.push(city[s][0]);
    while(q.size())
    {
        node now=q.top();q.pop();
        int u=now.id,x=now.cnt;
    //    cout<<"no "<<u<<" "<<x<<" "<<now.dist<<endl; 
        if(vis[u][x])
            continue;
        vis[u][x]=1;    
    //    cout<<"yes "<<u<<" "<<x<<" "<<now.dist<<endl; 
        for(int i=head[u];i;i=p[i].nxt)
        {
            int v=p[i].to;
        //    cout<<"nice "<<u<<" "<<v<<endl;
            if(city[v][x].dist>city[u][x].dist+p[i].val)//不免费 
            {
                city[v][x].dist=city[u][x].dist+p[i].val;
                city[v][x]={v,x,city[v][x].dist};
                q.push(city[v][x]);
            }
            if(x+1<=k&&city[v][x+1].dist>city[u][x].dist)//免费 
            {
                city[v][x+1].dist=city[u][x].dist;
                city[v][x+1]={v,x+1,city[v][x+1].dist};
                q.push(city[v][x+1]);
            }
        }
    }
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read(),m=read(),k=read();
    s=read(),t=read();
    for(int i=1;i<=m;i++)
    {
        int x=read(),y=read();
        ll z=read();
        add(x,y,z),add(y,x,z);
    }
    Dijkstra();
    ans=INF;
    for(int i=0;i<=k;i++)
        ans=min(ans,city[t][i].dist);
    printf("%lld\n",ans);
    fclose(stdin);
    fclose(stdout);
    return 0;
}

 

 

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
#define INF 0x3f3f3f3f
#define maxn 110005
#define maxm 2500001
inline ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ll)(ch-'0');ch=getchar();}
    return x*f;
} 
bool vis[maxn];
int head[maxn];
ll dis[maxn];
struct edge
{
    int to,nxt;
    ll val;
}p[maxm];
int n,m,k,tot,s,t,cnt;
typedef pair <ll,int> pa;
priority_queue <pa,vector<pa>,greater<pa> > q;

void add(int x,int y,ll z)
{
    ++cnt,p[cnt].to=y,p[cnt].val=z,p[cnt].nxt=head[x],head[x]=cnt;
}

void Dijkstra()
{
    memset(dis,INF,sizeof(dis));
    dis[s]=0;

    q.push(make_pair(0,s));
    while(q.size())
    {
        int u=q.top().second;q.pop();
        if(vis[u])
            continue;
        vis[u]=1;
        for(int i=head[u];i;i=p[i].nxt)
        {
            int v=p[i].to;
            if(dis[v]>dis[u]+p[i].val)
            {
                dis[v]=dis[u]+p[i].val;
                q.push(make_pair(dis[v],v));
            }
        }
    }
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read(),m=read(),k=read();
    s=read(),t=read();
    for(int i=1;i<=m;i++)
    {
        int x=read(),y=read();
        ll  z=read();
        add(x,y,z),add(y,x,z);
        for(int j=1;j<=k;j++)//虚拟节点和边 
        {    
            add((j-1)*n+x,y+j*n,0);//免费的边 
            add((j-1)*n+y,x+j*n,0);
            add(j*n+x,j*n+y,z),//不免费的边 
            add(j*n+y,j*n+x,z);
        }
    }
    Dijkstra();
    printf("%lld\n",dis[t+k*n]);
    fclose(stdin);
    fclose(stdout);
    return 0;
}

 

习题报告：

　　改造路：https://www.luogu.org/problemnew/show/P2939

　　 解题思路：和飞行路线一样的，只需要改一下数组大小以及起点和终点就行了。

 

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
#define INF 0x3f3f3f3f
#define maxn 10009
#define maxm 50009
inline ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ll)(ch-'0');ch=getchar();}
    return x*f;
} 
bool vis[maxn][29];
int head[maxn];
struct edge
{
    int to,nxt;
    ll val;
}p[maxm<<1];
struct node
{
    int id,cnt;
    ll dist;
    bool operator < (const node& temp) const
    {
        return dist>temp.dist;    
    } 
}dis[maxn][29];
int n,m,k,tot,s,t,cnt;
ll ans;

priority_queue<node>q;

void add(int x,int y,ll z)
{
    ++cnt,p[cnt].to=y,p[cnt].val=z,p[cnt].nxt=head[x],head[x]=cnt;
}

void Dijkstra()
{
    for(int i=0;i<=n;i++)
        for(int j=0;j<=k;j++)
            dis[i][j].dist=INF;
    dis[s][0]={s,0,0};
    q.push(dis[s][0]);
    while(q.size())
    {
        node now=q.top();q.pop();
        int u=now.id,x=now.cnt;
        if(vis[u][x])
            continue;
        vis[u][x]=1;
        for(int i=head[u];i;i=p[i].nxt)
        {
            int v=p[i].to;
            if(dis[v][x].dist>dis[u][x].dist+p[i].val)
            {
                dis[v][x].dist=dis[u][x].dist+p[i].val;
                dis[v][x]={v,x,dis[v][x].dist};
                q.push(dis[v][x]);
            }    
            if(x+1<=k&&dis[v][x+1].dist>dis[u][x].dist)
            {
                dis[v][x+1].dist=dis[u][x].dist;
                dis[v][x+1]={v,x+1,dis[v][x+1].dist};
                q.push(dis[v][x+1]);
            }
        } 
    }
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read(),m=read(),k=read();
    s=1,t=n; 
    for(int i=1;i<=m;i++)
    {
        int x=read(),y=read();
        ll  z=read();
        add(x,y,z),add(y,x,z);
    }
    Dijkstra();
    ans=INF;
    for(int i=0;i<=k;i++)
        ans=min(ans,dis[t][i].dist);
    printf("%lld\n",ans);
    fclose(stdin);
    fclose(stdout);
    return 0;
}