2椭圆曲线密码学:有限域和离散对数

原文链接：https://andrea.corbellini.name/2015/05/23/elliptic-curve-cryptography-finite-fields-and-discrete-logarithms/

这篇文章是ECC系列的第二篇。

在前一篇文章中，我们已经看到了如何基于实数域上的椭圆曲线来定义一个群。具体如下，我们定义了点的加法规则：给定三个共线的点，它们的和是零（P+Q+R=0）然后推导出计算机中点的加法的一个几何方法和一个代数方法（几何加法和代数加法）。

接着我们介绍了标量乘法()，并发现了一个计算标量乘法的“易解”算法：“加倍（double）和相加（add）”。

现在我们将椭圆曲线限制在有限域内，而不是实数域，看看情况如何变化。

模p的整数域（The field of integers modulo p）

一个有限域，首先是一个包含有限个元素的集合。有限域的一个例子是模p的整数集，其中p是素数。它通常表示为或，我们将使用最后一种符号。

在域中，我们有两种二元运算：加法(+)和乘法(·)。它们都具有封闭性，结合律和交换律。对于这两种运算，每个元素都存在一个唯一的单位元，并且每个元素都存在一个唯一的逆元。最后，乘法是对加法的分配：。

整数模p的集合由整数0到p-1组成。加法和乘法在运算(也称为“时钟运算”)中工作。这里有一些运算的例子：

• 加法：（18+9）mod23=4
• 减法：（7-14）mod23=16
• 乘法：4·7mod23=5
• 加法逆元：-5mod23=18　　实际：（5+（-5））mod23=（5+18）mod23=0
• 乘法逆元：9^-1mod23=18　　实际：9·9^-1mod23=9·18mod23=1

如果这些方程看起来不熟悉，你需要一个模块化的运算入门，看看 Khan Academy。

正如我们已经说过的，模p的整数集是一个域，因此上面列出的所有属性都成立。注意，p是素数的要求是很重要的！（p=4）对4取模的整数集不是一个域：2没有乘法逆元（如：等式2·xmod4=1没有结果）

 模p除法（Division modulo p）

 我们将定义在上的椭圆曲线，但是在这之前我们需要弄清楚中的含义。简单说，,即，x/y等于x乘以y的乘法逆元。这个事实并不意外，它给了我们一个基本的除法：找到该数的乘法逆元，然后进行乘法运算。

用扩展的欧几里德算法（extended Euclidean algorithm）可以“轻松”计算乘法逆元，其中，最坏的情况下时间复杂度为（或者如果我们考虑p的比特长度的话，最坏的情况则是）。

我们不讨论扩展的欧几里得算法的细节，因为它离题了，但是这里有一个有效的的Python实现：

def extended_euclidean_algorithm(a, b):
    """
    Returns a three-tuple (gcd, x, y) such that
    a * x + b * y == gcd, where gcd is the greatest
    common divisor of a and b.

    This function implements the extended Euclidean
    algorithm and runs in O(log b) in the worst case.
    """
    s, old_s = 0, 1
    t, old_t = 1, 0
    r, old_r = b, a

    while r != 0:
        quotient = old_r // r
        old_r, r = r, old_r - quotient * r
        old_s, s = s, old_s - quotient * s
        old_t, t = t, old_t - quotient * t

    return old_r, old_s, old_t


def inverse_of(n, p):
    """
    Returns the multiplicative inverse of
    n modulo p.

    This function returns an integer m such that
    (n * m) % p == 1.
    """
    gcd, x, y = extended_euclidean_algorithm(n, p)
    assert (n * x + p * y) % p == gcd

    if gcd != 1:
        # Either n is 0, or p is not a prime number.
        raise ValueError(
            '{} has no multiplicative inverse '
            'modulo {}'.format(n, p))
    else:
        return x % p

 

 

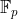上的椭圆曲线

现在我们可以将椭圆曲线定义在上。在上一篇文章中我们定义了实数域上的椭圆曲线：

现在转变成：

其中0仍然是无穷远处的点，a和b是中的整数。

 

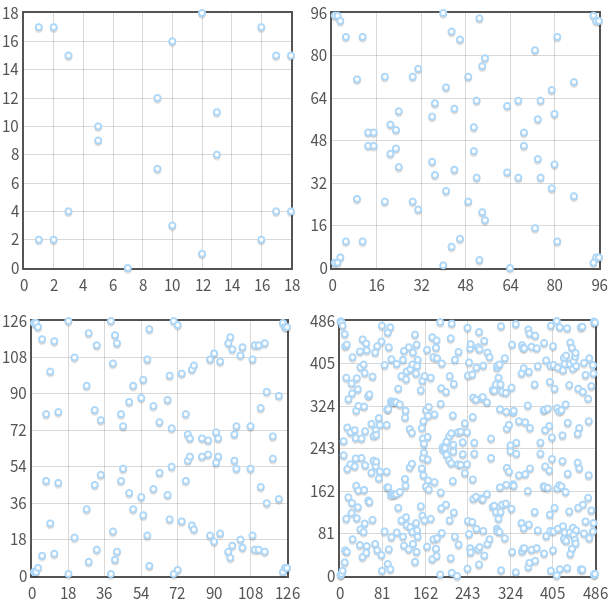
图 1 上图是曲线在参数p分别为19,97,127,487时的图形。注意，对于每一个x，最多有两个对应点，还要注意处的对称性

 

 

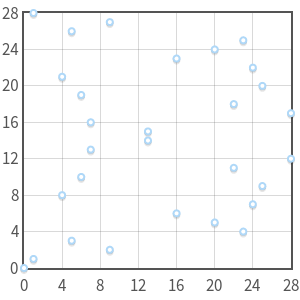
 图 2 曲线是奇异的，其中有一个三重点（0,0）。它不是一条有效的椭圆曲线

之前实数域上的连续曲线现在转变为xy平面上的一组不相交的点的集合。但是我们可以证明，即使我们限制了定域，中的椭圆曲线（的点集）仍然是一个阿贝尔群。

点的加法

显然，我们需要稍微改变一下加法的定义来让它在上生效。对于实数，我们说过三个共线的点之和为零（P+Q+R=0）我们可以保留这个定义，但是我们该如何理解这三个点在中共线？

我们可以说如果有一条直线连接三个点，则这三点共线。当然，中的直线和中的直线不一样，非正式地说，中的直线是满足等式（这是标准直线方程，加上modp）的点(x,y)的集合。

 

 

图 3 曲线上的点的加法，P=(16,20)和Q=(41,120)。注意连接这些点的直线是如何在平面上“重复”的

 假设我们在一个群中，点的加法保留了我们已知的性质：

• (来自单位元的定义)
• 给定一个非零的点Q，逆元-Q是横坐标相等但纵坐标相对的点。或者，如果你愿意，。举个例子，上的曲线上有点Q(2,5)，它的逆元
•  而且，（来自逆元的定义）

 代数和

计算点的加法的表达式与前一篇文章完全相同，除了我们需要在每个表达式的末尾加上“modp”。

 因此，给定，和，我们可以如下计算：

如果，斜率m为:

 

 否则，如果，斜率m为：

 

 这些公式没有改变并不是巧合：事实上，这些公式适用于每一个域（除了和，它们是特殊的）。现在我觉得我必须为这个事实提供一个证明。问题是：群公理的证明通常涉及复杂的数学概念。然而，我从proof from Stefan Friedl 那里找到了一个只使用基本概念的证明。如果你对为什么这些公式(几乎)适用于每个域感兴趣，请阅读它。

 回到我们这里，我们不会定义一个几何方法：事实上，它有一些问题。例如，在之前的文章中，我们说过要计算P+P，我们需要在P中取曲线的切线。但是如果没有连续性，“切线”这个词就没有任何意义。我们可以解决这个问题和其他问题，但是单纯的几何方法太复杂了，一点也不实用。

 相反地，您可以使用我编写的用于计算点的加法的交互式工具 interactive tool 。

 椭圆曲线群的阶

我们说过，定义在有限域上的椭圆曲线有有限个数的点。我们需要回答的一个重要问题是:到底有多少个点?

首先，假设一组中的点的数量称为组的阶数。

x从0到p-1的所有可能值遍历并不是一种可行的计数方法，因为它需要O（p）步，如果p是一个大素数，这是“难解”的。

 幸运的是，有一种更快的计算顺序的算法: Schoof's algorithm。算法的细节我就不讲了，重要的是它的运行时间是多项式时间，这就是我们需要的。

 标量乘法和循环子群

 与实数一样，乘法可以定义为:

同样，我们可以使用“加倍（double）和相加（add）”算法来执行O(logn)步的乘法运算(或者O(k), k是n的位数)。我还写了一个用于标量乘法的交互式工具 interactive tool 。

 上的椭圆曲线上点的乘法有一个有趣的性质。取曲线和点。现在计算P的所有倍数：

 

 

 

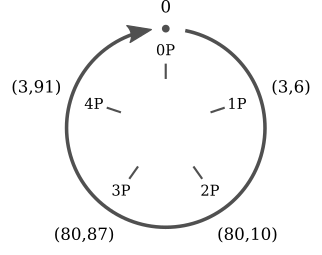
图 4 P的倍数只是5个不同的点(0，P，2P，3P，4P)，它们是循环重复的。很容易发现椭圆曲线上的标量乘法和模运算中的加法之间的相似性

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• ...

在这里我们可以立即发现两件事:首先，P的倍数只有5：椭圆曲线的其他点永远不会出现。其次，它们是周期性重复的。我们可以写成：

• 
• 
• 
• 
• 

对每一个整数k。注意，由于模运算符，这五个等式可以被“压缩”成一个单独的等式：

不仅如此，我们还可以立即证明这五个点在加法下是封闭的。也就是说，无论我加0，P，2P，3P或4P，结果总是这五个点中的一个。同样，椭圆曲线的其他点永远不会出现在结果中。

每个点都是一样的，不仅仅是P=(3,6)。实际上，如果我们取一个一般的P：

这意味着：如果我们把两个P的倍数相加，得到一个P的倍数(即P的倍数在加法下是封闭的)。这足以证明P的倍数的集合是由椭圆曲线构成的群的一个循环子群。

“子群”是另一个群的子集。“循环子群”是一个元素循环重复的子群，就像我们在前面的例子中所展示的那样。点P称为循环子群的产生点或基点。循环子群是ECC和其他密码学的基础。我们将在下一篇文章中看到原因。

子群的阶

我们可以问自己点P生成的子群的阶数是多少(或者说，P的阶数是多少)要回答这个问题，我们不能使用Schoof算法，因为该算法只适用于整个椭圆曲线，而不适用于子群。在解决这个问题之前，我们需要更多的信息：

到目前为止，我们已经定义了一组点的个数的顺序。这个定义仍然有效，但是在一个循环子群中，我们可以给出一个新的等价定义：P的阶是使nP=0的最小正整数n。事实上，如果你看前面的例子，我们的子组包含5个点，我们有5P=0。

通过拉格朗日定理，P的阶与椭圆曲线的阶联系起来，该定理指出子群的阶是父群的阶的除数。换句话说，如果一条椭圆曲线包含N个点，并且它的一个子群包含n个点，则n是N的除数。

这两个信息一起给我们提供了一种找出具有基点P的子群的阶的方法：

1. 利用Schoof算法计算椭圆曲线的阶N
2. 求出N的所有因子
3. 对于每个N的因子n ，计算nP
4. 使nP=0的最小n是子群的阶数

举个例子，域上的曲线。它的子组可能有阶1,2,3,6,7,14,21或42。如果我们尝试P=(2,3)我们会发现P≠0，2P≠0，...7P＝0，因此P的阶n=7。

注意，重要的是取最小的除数，而不是随机的除数。如果我们随机进行，我们可以取n=14，14不是子群的阶，而是它的倍数之一。

另一个例子，由域上的等式定义的椭圆曲线有阶N=37，37也是一个素数。它的子群可能只有n=1或n=37阶。你很容易猜到，当n=1时，子群只包含无穷远处的点；当n=N时，该子群包含了椭圆曲线的所有点。

找基点

对于我们的ECC算法，我们想要高阶子群。所以一般我们会选择一条椭圆曲线，计算它的阶数N，选择一个高除数作为子群的阶数n，最后找到一个合适的基点。也就是说：我们不会选择一个基点然后计算它的阶，但我们会做相反的事情：我们会首先选择一个看起来足够好的阶，然后我们会寻找一个合适的基点。我们怎么做呢？

首先，我们需要再介绍一个术语。拉格朗日定理表明，数字h=N/n总是一个整数(因为n是N的除数)。数字h有个名字：它是子群的余子式。

现在考虑对于椭圆曲线上的每一点我们有NP=0。这是因为N是任意候选数n的倍数。利用余子式的定义，我们可以这样写：

现在假设n是一个素数(原因将在下一篇文章中解释，我们更喜欢素数)。这个等式，写成这种形式，告诉我们点G=hP产生了一个n阶的子群(G=hP=0时除外，这种情况下子群是1阶的)。

因此，我们可以概括出以下算法：

1. 计算椭圆曲线的阶N
2. 选择子群的阶n。为了使算法有效，这个数必须是素数并且必须是N的除数
3. 计算余子式h =N/ n
4. 在曲线上随机选择点P
5. 计算G =hP
6. 如果G为0，则返回步骤4。否则我们就找到了阶为n且余子式为h的循环子群的基点。

注意，这个算法只适用于n是素数的情况。如果n不是素数，那么G的阶数可以是n的因数之一。

离散对数

正如我们在学习连续的椭圆曲线时所做的那样，我们现在要讨论的问题是：如果我们知道P和Q, 那该如何获得k使得Q=kP？

这个问题被称为椭圆曲线的离散对数问题，被认为是一个“难解”的问题，因为没有已知的多项式时间算法可以在普通的计算机上解出来。然而，这一信念并没有数学依据。

这个问题也类似于其他密码学的离散对数问题，如数字签名算法(DSA)，迪菲-海尔曼密钥交换(D-H)和海尔曼密钥交换(D-H)和EIGamal算法——它们有相同的名字并不是巧合。不同的是，在这些算法中，我们使用模取幂代替标量乘法。他们的离散对数问题可以表述为：如果我们知道a和b，如何求k使得？

这两个问题都是“离散的”，因为它们涉及有限域(更准确地说，是循环子群)。它们是“对数”因为它们类似于普通的对数。

ECC的有趣之处在于，与密码学中使用的其他类似问题相比，椭圆曲线的离散对数问题似乎“更难”。这意味着为了达到与其他密码学相同的安全级别，整数k需要更少的位，我们将在本系列的第四篇也是最后一篇文章中详细介绍这一点。

 下周见

 今天的学习内容足够了！我真的希望你喜欢这篇文章。如果由不懂得地方，请写下评论。下周的文章将是本系列的第三篇，内容是关于ECC算法：密钥对生成、ECDH和ECDSA。这将是本系列中最有趣的部分之一。不要错过它！

 Read the next post of the series »