2017-2018 ACM-ICPC, Asia Daejeon Regional Contest Solution

A：Broadcast Stations

留坑。

 

B：Connect3

题意：四个栈，每次放棋子只能放某个栈的栈顶，栈满不能放，现在给出(1, x) 表示黑子放在第x个栈的第一个位置，白子放在第b个栈的第a个位置并且是胜利局势的情况有几种，只要有三个相同的连在一起就是赢了

思路：数据很小，暴力搜索即可，注意判重。

  1 #include <bits/stdc++.h>
  2 
  3 using namespace std;
  4 
  5 int x, a, b;
  6 
  7 int G[10][10];
  8 
  9 // 0 not done
 10 // 1 white
 11 // 2 black
 12 
 13 inline string Hash()
 14 {
 15     string ans = "";
 16     for (int i = 1; i <= 4; ++i)
 17         for (int j = 1; j <= 4; ++j)
 18         {
 19             ans += G[i][j] + '0'; 
 20         }
 21     return ans;
 22 }
 23 
 24 map <string, bool> mp;
 25 
 26 int cnt[10];  
 27 
 28 inline bool ok(int x, int y)
 29 {
 30     if (x < 0 || x > 4 || y < 0 || y > 4) return false;
 31     return true;
 32 }
 33 
 34 int Move[][2] = 
 35 {
 36      0,  1,
 37      0, -1,
 38      1,  0,
 39     -1,  0,
 40     -1, -1,
 41     -1,  1,
 42      1, -1,
 43      1,  1,
 44 };
 45 
 46 inline bool check(int x, int y)
 47 {
 48     int color = G[x][y];
 49     for (int i = 0; i < 8; ++i)
 50     {
 51         int nx = x + Move[i][0];
 52         int ny = y + Move[i][1];
 53         int nnx = nx + Move[i][0];
 54         int nny = ny + Move[i][1];
 55         if (ok(nx, ny) && ok(nnx, nny))
 56             if (G[nx][ny] == color && G[nnx][nny] == color) 
 57                 return true;
 58         nx = x + Move[i][0];
 59         ny = y + Move[i][1];
 60         nnx = x - Move[i][0];
 61         nny = y - Move[i][1];
 62         if (ok(nx, ny) && ok(nnx, nny))
 63             if (G[nx][ny] == color && G[nnx][nny] == color)
 64                 return true;
 65     }        
 66     return false;
 67 }
 68 
 69 int tot;
 70 
 71 inline void DFS(int x, int y, int vis)
 72 {
 73     if (check(x, y))
 74     {
 75         if (vis == 1) return;
 76         if (x == b && y == a) 
 77         {
 78             string s = Hash();
 79             if(mp[s] == false)
 80             {
 81                 mp[s] = true;
 82                 tot++;
 83             }
 84         }
 85         return;
 86     }
 87 //    if (x == b && y == a)
 88 //    {
 89 //        if (check())
 90 //        {
 91 //            string s = Hash();
 92 //            if (mp[s] == false)
 93 //            {
 94 //                mp[s] = true;
 95 //                tot++;
 96 //            }
 97 //        }
 98 //        return;
 99 //    }
100     for (int i = 1; i <= 4; ++i)
101     {
102         if (cnt[i] < 4)
103         {
104             cnt[i]++;
105             G[i][cnt[i]] = vis;
106             DFS(i, cnt[i], vis == 1 ? 2 : 1);
107             G[i][cnt[i]] = 0;
108             cnt[i]--; 
109         }
110     }
111 }
112 
113 inline void Init()
114 {
115     memset(cnt, 0, sizeof cnt);
116        memset(G, 0, sizeof G);    
117     mp.clear();
118     tot = 0;
119 }
120 
121 
122 int main()
123 {
124     while (scanf("%d%d%d", &x, &a, &b) != EOF)
125     {
126         Init();
127         cnt[x]++; G[x][1] = 2;
128         DFS(x, 1, 1);
129         cout << tot << endl;
130     }
131 }
View Code

 

C：Game Map

题意：给出n个点，以及m条无向边，然后两个点之间如果有边那么度数大的那个点可以走到度数小的那个点，求最后从任意一个点出发，最远能走的路径的长度。

思路：显然，重新建图之后两个点之间最多有一个边，那么显然是若干棵树的结构，树形DP即可

 1 #include<bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 #define N 100010
 6 #define M 1000010
 7 
 8 struct node{
 9     int v,nx;
10     inline node(){}
11     inline node(int v,int nx) :v(v), nx(nx){}
12 }G[M];
13 
14 int n, m;
15 int head[N], vis[N], dp[N], du[N], ans;
16 int tot;
17 
18 inline void init()
19 {
20     tot = 0;
21     memset(head, -1, sizeof head);
22     memset(vis, 0, sizeof vis);
23     memset(dp, 0, sizeof dp);
24     memset(du, 0, sizeof du);
25 }
26 
27 inline void addedge(int u,int v)
28 {
29     G[tot] = node(v, head[u]);
30     head[u] = tot++;
31     G[tot] = node(u, head[v]);
32     head[v] = tot++;
33 }
34 
35 inline void DFS(int u)
36 {
37     dp[u] = 1;
38     vis[u] = 1;
39     int tmp = 0;
40     for(int i = head[u]; ~i; i = G[i].nx)
41     {
42         int v = G[i].v;
43         if(du[v] > du[u])
44         {
45             if(!vis[v]) DFS(v);
46             tmp = max(tmp, dp[v]);
47         }    
48     }
49     dp[u] += tmp;
50     ans = max(ans, dp[u]);
51 }
52 int main()
53 {
54     while(~scanf("%d %d",&n,&m))
55     {
56         init();
57         for(int i = 1; i <= m; ++i)
58         {
59             int u,v;
60             scanf("%d %d",&u,&v);
61             addedge(u, v);
62             du[u]++;
63             du[v]++;
64         }
65         for(int i = 0; i < n; ++i)
66         {
67             if(!vis[i]) DFS(i);
68         }
69         printf("%d\n", ans);
70     }
71     return 0;
72 }
View Code

 

D：Happy Number

水。

 1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 map <int, bool> mp;
 6 
 7 int n;
 8 
 9 inline int Get(int x)
10 {
11     int tot = 0;
12     while (x)
13     {
14         int num = x % 10;
15         tot += num * num;
16         x /= 10;
17     }
18     return tot;
19 }
20 
21 inline bool solve()
22 {
23     mp.clear();
24     while (true)
25     {
26         int num = Get(n);
27         if (num == 1) return true;
28         n = num;
29         if (mp[num] == true)
30             return false;
31         mp[num] = true;
32     }
33 }
34 
35 int main()
36 {
37     while (scanf("%d", &n) != EOF)
38     {
39         puts(solve() ? "HAPPY" : "UNHAPPY");
40     }
41 }
View Code

 

 

E：How Many to Be Happy?

题意：定义一个函数H(e), 如果一条边属于最小生成树，那么H(e) = 0, 如果不属于，那么H(e) = 删掉最少的边使得它是最小生成树的边数

思路：考虑最小生成树任意两点之间都相互连通，那么对于每一条边，我们需要知道这条边邻接的两点，在包含这条边以及权值比这条边小的所有边的图中的最小割是多少，对每一条边都这么跑一次最大流

  1 #include <bits/stdc++.h>
  2 
  3 using namespace std;
  4 
  5 #define N 110
  6 #define M 510
  7 #define INF 0x3f3f3f3f
  8 
  9 struct Edge
 10 {
 11     int to, nx, cap, flow;
 12     inline Edge() {}
 13     inline Edge(int to, int nx, int cap, int flow) : to(to), nx(nx), cap(cap), flow(flow) {}
 14 }edge[M << 1];
 15 
 16 int head[N], tol;
 17 
 18 inline void Init()
 19 {
 20     tol = 2;
 21     memset(head, -1, sizeof head);
 22 }
 23 
 24 inline void addedge(int u, int v, int w)
 25 {
 26     edge[tol] = Edge(v, head[u], w, 0); head[u] = tol++;
 27     edge[tol] = Edge(u, head[v], w, 0); head[v] = tol++; 
 28 }
 29 
 30 int Q[N];
 31 int dep[N], cur[N], sta[N];
 32 
 33 inline bool BFS(int s, int t, int n)
 34 {
 35     int front = 0, tail = 0;
 36     memset(dep, -1, sizeof (dep[0]) * (n + 2));
 37     dep[s] = 0;
 38     Q[tail++] = s;
 39     while (front < tail)
 40     {
 41         int u = Q[front++];
 42         for (int it = head[u]; ~it; it = edge[it].nx)
 43         {
 44             int v = edge[it].to;
 45             if (edge[it].cap > edge[it].flow && dep[v] == -1)
 46             {
 47                 dep[v] = dep[u] + 1;
 48                 if (v == t) return true;
 49                 Q[tail++] = v;
 50             }
 51         }
 52     }
 53     return false;
 54 }
 55 
 56 inline int Dinic(int s, int t, int n)
 57 {
 58     int maxflow = 0;
 59     while (BFS(s, t, n))
 60     {
 61         for (int i = 0; i < n; ++i) cur[i] = head[i];
 62         int u = s, tail = 0;
 63         while (cur[s] != -1)
 64         {
 65             if (u == t)
 66             {
 67                 int tp = INF;
 68                 for (int i = tail - 1; i >= 0; --i)
 69                     tp = min(tp, edge[sta[i]].cap - edge[sta[i]].flow);
 70                 maxflow += tp;
 71                 for (int i = tail - 1; i >= 0; --i)
 72                 {
 73                     edge[sta[i]].flow += tp;
 74                     edge[sta[i] ^ 1].flow -= tp;
 75                     if (edge[sta[i]].cap - edge[sta[i]].flow == 0)
 76                         tail = i;
 77                 }
 78                 u = edge[sta[tail] ^ 1].to;
 79             }
 80             else if (cur[u] != -1 && edge[cur[u]].cap > edge[cur[u]].flow && dep[u] + 1 == dep[edge[cur[u]].to])
 81             {
 82                 sta[tail++] = cur[u];
 83                 u = edge[cur[u]].to;
 84             }
 85             else
 86             {
 87                 while (u != s && cur[u] == -1)
 88                     u = edge[sta[--tail] ^ 1].to;
 89                 cur[u] = edge[cur[u]].nx;
 90             }
 91         }
 92     }
 93     return maxflow;
 94 }
 95 
 96 struct node
 97 {
 98     int u, v, w;
 99     inline void scan()
100     {
101         scanf("%d%d%d", &u, &v, &w);
102         u--, v--;
103     }
104     inline bool operator < (const node& r) const
105     {
106         return w < r.w;
107     }
108 }G[M];
109 
110 int n, m;
111 
112 int main()
113 {
114     while (scanf("%d%d", &n, &m) != EOF)
115     {
116         for (int i = 1; i <= m; ++i)
117             G[i].scan();
118         sort(G + 1, G + 1 + m);
119         int ans = 0;
120         for (int i = 1; i <= m; ++i)
121         {
122             Init();
123             for (int j = 1; j < i; ++j)
124             {
125                 if (G[j].w >= G[i].w)
126                     break;
127                 addedge(G[j].u, G[j].v, 1);
128             }
129             ans += Dinic(G[i].u, G[i].v, n);
130 //            cout << G[i].u << " " << G[i].v << " " << ans << endl;
131         }
132         cout << ans << endl;
133     }    
134     return 0;
135 }
View Code

 

 

F：philosopher's Walk

题意：给出n=2^k，m<=2^2k。对于一个n*n的图，输出第m个点的坐标。

思路：因为每个n*n的图由4个全等的(n/2)*(n/2)的图组成，所以采用分治的思想，每次算出目标点在4块图的那一块，记录那块图的坐标。

但是因为子图的方向不一样，所以要在计算出第几块图之后，要根据之前的方向判断这块图在左上，左下，右上，右下那个位置。

 

 1 #include<bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 int main() {
 6     long long n,m,x,y,t,p,q;
 7     while (scanf("%lld %lld",&n,&m)!=EOF) 
 8     {
 9         x=y=1;    t=1;
10         while (n>1) {
11             q=n*n/4;
12             p=(m-1)/q+1;
13             m=(m-1)%q+1;
14             if (t==1) {
15                 if (p==1) {t=2;}
16                 else if (p==2) {y+=(n/2);}
17                 else if (p==3) {x+=(n/2); y+=(n/2);}
18                 else if (p==4) {x+=(n/2); t=4;}
19             }
20             else if (t==2) {
21                 if (p==1) {t=1;}
22                 else if (p==2) {x+=(n/2);}
23                 else if (p==3) {x+=(n/2); y+=(n/2);}
24                 else if (p==4) {y+=(n/2); t=3;}
25             }
26             else if (t==3) {
27                 if (p==1) {x+=(n/2); y+=(n/2); t=4;}
28                 else if (p==2) {x+=(n/2);}
29                 else if (p==4) {y+=(n/2); t=2;}
30             }
31             else if (t==4) {
32                 if (p==1) {x+=(n/2); y+=(n/2); t=3;}
33                 else if (p==2) {y+=(n/2);}
34                 else if (p==4) {x+=(n/2); t=1;} 
35             }
36             n/=2;
37         }
38         printf("%lld %lld\n",x,y);
39     }
40     return 0;
41 }
View Code

 

 

G：Rectilinear Regions

留坑。

 

H：Rock Paper Scissors

留坑。

 

I：Slot Machines

题意：寻找下标为k长度为p的循环节，使得k+p最小，在k+p相同时保证p小。

思路：倒过来寻找，Next[i]记录上一个和这一位数字相同的下标。每次寻找都找前一位的Next中其中一位，并且保证这一位后面与当前节点值相同，从而保证了Next数组里面记录了循环的初始节点，最后扫一遍即可。

 1 #include<bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 #define N 1000010
 6 #define INF 0x3f3f3f3f
 7 
 8 int n;
 9 int arr[N], nx[N];
10 
11 int main()
12 {
13     while(~scanf("%d",&n))
14     {
15         memset(nx, 0, sizeof nx);
16         for(int i = n; i >= 1; --i)
17         {
18             scanf("%d", arr + i);
19         }
20         for(int i = 2; i <= n; ++i)
21         {
22             int tmp = nx[i - 1];
23             while(tmp != 0 && arr[i] != arr[tmp + 1])
24                 tmp = nx[tmp];
25             if(arr[i] == arr[tmp + 1])
26                 tmp++;
27             nx[i] = tmp;
28         }
29         int sum = INF;
30         int ansk = 0;
31         int ansp = 0;
32         for(int i = 1; i <= n; ++i)
33         {
34             int k = n - i;
35             int p = i - nx[i];
36             if(k + p < sum)
37             {
38                 sum = k + p;
39                 ansk = k;
40                 ansp = p;
41             }
42             else if(sum == k + p && p < ansp)
43             {
44                 ansk = k;
45                 ansp = p;
46             }
47         }
48         printf("%d %d\n",ansk, ansp);
49     }
50     return 0;
51 }
View Code

 

 

J：Strongly Matchable

留坑。

 

K：Untangling Chain

题意：给出n个线段，每次给出线段的长度和转向的方向 1 表示左转，-1 表示右转，可以修改线段的长度,长度为(1 -> n) 使得所有线段不相交

思路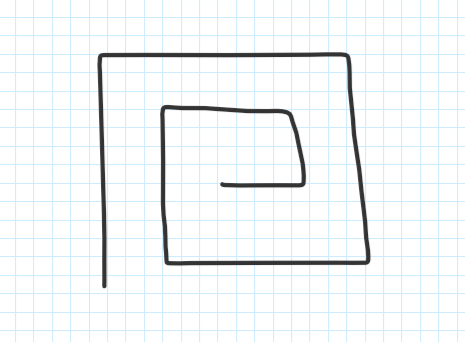： 按照类似这样的方法构造一下，每次的长度最多+1，长度最大为n，符合题意。 图中只是一个方向的实例，构造的图不一定是这样，但是思路是这样。 

 1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 int n;
 6 
 7 int up, down, l, r;
 8 int x, y, dir;
 9 
10 // 0 up 1 left 2 down 3 right
11 
12 int main()
13 {
14     while (scanf("%d", &n) != EOF)
15     {
16         up = down = l = r = 0;
17         x = y = dir = 0;
18         int len, num;
19         for (int i = 1; i <= n; ++i)
20         {
21             scanf("%d%d", &len, &num);
22             dir = (dir + 4) % 4;
23             if (dir == 0)
24             {
25                 len = up - y + 1;
26                 y += len;
27                 up = max(up, y);
28             }
29             else if (dir == 1)
30             {
31                 len = x - l + 1;
32                 x -= len;
33                 l = min(l, x);
34             }
35             else if (dir == 2)
36             {
37                 len = y - down + 1;
38                 y -= len;
39                 down = min(down, y);
40             }
41             else if (dir == 3)
42             {
43                 len = r - x + 1;
44                 x += len;
45                 r = max(r, x);
46             }
47             printf("%d%c", len , " \n"[i == n]);
48             dir += num;
49         }
50     }
51     return 0;
52 }
View Code

 

J：Vacation Plans

留坑。

 

 

赛后总结：

  • 如果开了某一题但是没有思路，读新题的优先级高于一切
  • 比赛过程尽量不要懈怠，不一定无题可做， 不要从心里上战败
  • 做题要看清数据范围，算一算时间复杂度，有些题确实可以爆搜
  • 写题的时候，如果开了两个一样的东西，一定要万分注意，要知道什么时候用哪个
  • 当没有什么思路的时候，模拟一下题意过程是比较好的一个方式
  • 一道题如果没有思路，但是感觉像某种算法的题，可以考虑弃题，不要停留太久浪费时间，读新题
  • 对于题面又臭又长的题目，一定要耐心下来读
  • 当一题队友在敲，但是思维有一点阻碍时，可以适当放下手中事，帮队友理清一下思路可能会更好
  • 构造题有时候要大胆，但是构造题以及猜想题没有百分百把握下，不可开场做

 

posted @ 2018-08-12 19:27  Dup4  阅读(711)  评论(0)  编辑  收藏  举报