ZOJ - 1504 Slots of Fun 【数学】
题目链接
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=1504
题意
给出一串字符串 里面的每个字符的位置 都按照题目的意思 给出
求哪些字母 所在的位置 随意三个点 是否能构成 一个 正三角形 如果能 就输出这个字母 最后输出的结果 要按照字典序
思路
难点在于 给这些字母赋予坐标
我们可以从最底层 来赋值
最底层的 Y坐标都是1 X坐标分别是 `1, 2, 3, 4
然后往上走 的坐标 都是右 下一层的两个坐标决定的
X的坐标 是 下一层两个坐标的终点 Y坐标是下面一层坐标Y坐标+ sqrt(3)/2
数据范围很小 用 O(n^3) 暴力 都是可以过的
AC代码
#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <map>
#include <stack>
#include <set>
#include <numeric>
#include <sstream>
#include <iomanip>
#include <limits>
#define CLR(a, b) memset(a, (b), sizeof(a))
#define pb push_back
using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
typedef pair<string, int> psi;
typedef pair<string, string> pss;
const double PI = acos(-1.0);
const double E = exp(1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const int maxn = 4e5 + 5;
const int MOD = 1e9 + 7;
struct node
{
double x, y;
int c;
}q[12][12];
double dis(node a, node b)
{
double ans = sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
return ans;
}
bool EPS(double x, double y)
{
if (fabs(x - y) < eps)
return true;
return false;
}
bool equil(node a, node b, node c)
{
double Dis1 = dis(a, b);
double Dis2 = dis(a, c);
double Dis3 = dis(b, c);
if (EPS(Dis1, Dis2) && EPS(Dis1 , Dis3) && EPS(Dis2, Dis3))
return true;
return false;
}
int main()
{
int n;
while (scanf("%d", &n) && n)
{
string s;
cin >> s;
int len = s.size();
vector <node> c[26];
CLR(q, 0);
for (int i = 0, count = 0; i < n; i++)
{
for (int j = 0; j < i + 1; j++)
{
q[i][j].c = s[count++] - 'a';
}
}
for (int i = 0; i < n; i++)
{
q[n - 1][i].x = i + 1;
q[n - 1][i].y = 1;
c[q[n - 1][i].c].pb(q[n - 1][i]);
}
for (int i = n - 2; i >= 0; i--)
{
for (int j = 0; j <= i; j++)
{
q[i][j].y = q[i + 1][j].y + sqrt(3.0) * 1.0 / 2;
q[i][j].x = (q[i + 1][j].x + q[i + 1][j + 1].x) * 1.0 / 2;
c[q[i][j].c].pb(q[i][j]);
}
}
string ans = "";
for (int l = 0; l < 26; l++)
{
int len = c[l].size();
int flag = 0;
for (int i = 0; i < len; i++)
{
for (int j = 0; j < len; j++)
{
for (int k = 0; k < len; k++)
{
if (i != j && i != k && j != k && flag == 0)
{
if (equil(c[l][i], c[l][j], c[l][k]))
{
ans += l + 'a';
flag = 1;
}
}
}
}
}
}
if (ans == "")
printf("LOOOOOOOOSER!\n");
else
cout << ans << endl;
}
}


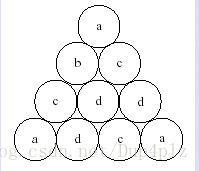

 浙公网安备 33010602011771号
浙公网安备 33010602011771号