2018-2019 ACM-ICPC, Asia Jiaozuo Regional Contest
Contest Info
[Practice Link](https://codeforces.com/gym/102028)
| Solved | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7/12 | O | - | O | O | O | - | O | O | - | - | Ø | - |
- O 在比赛中通过
- Ø 赛后通过
- ! 尝试了但是失败了
- - 没有尝试
Solutions
A. Xu Xiake in Henan Province
签到。
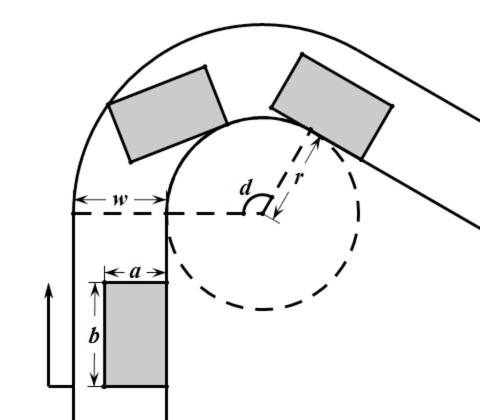
D. Keiichi Tsuchiya the Drift King
题意:
给出\(a, b, r, d\),求最小的\(w\)。
E. Resistors in Parallel
题意:
给出\(n\)个电阻,第\(i\)个电阻的阻值为$:
- \(i\)没有平方因子,阻值为\(i\)
- \(i\)有平方因子,阻值为\(\infty\)
现有\(n\)个集合,第\(i\)个集合的编号为\(i\),所有编号为\(j(j \;|\; i)\)的电阻都属于集合\(i\)。
一个集合的阻值为集合中所有电阻并联的电阻。
现在问阻值最小的集合是多少。
思路:
显然无穷大的电阻是没用的。
那么考虑答案集合为\(x\),那么该集合的阻值为:
其中\(j \;|\; i\)。
那么考虑变换式子,有:
那么就是:
那么只需要求\(x\)的因子和就可以了。
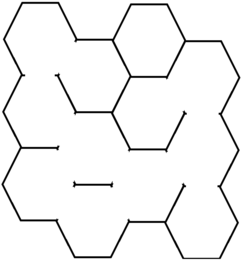
F. Honeycomb
题意:
给出恶心的蜂房,求\(S\)到\(T\)最小经过多少个房间。
思路:
找规律模拟即可。
H. Can You Solve the Harder Problem?
题意:
给出\(n\)个数,每个数的值域为\([1, 10^6]\),现在要求所有本质不同的连续子区间的最大值的和。
思路:
本质不同,可以想到先进行后缀排序,然后考虑当前后缀的开头固定,结尾是一段连续的区间。
再考虑在原序列中,每个点向它后面的第一个比它大的数连边,那么会形成一棵森林。
那么对于每段后缀\(i\),假设它的可选结尾范围为\([l_i, r_i]\),那么我们先找到\([i, l_i - 1]\)这段范围最大的数的下标,然后看这个数的父亲\(nx\)。
那么我们发现结尾\([l_i, nx]\)这段的最大值都是这个数。
然后后面的,就是树上一段到根的连续的东西,令边权为两个坐标相差的距离,那么每个点掌控的范围就是它到它父亲之间的那些点。
预处理一下贡献的前缀和,然后就可以\(O(1)\)计算了。
I. Distance
题意:
在一维数轴上给出\(n\)个点,告诉你\(i \rightarrow i + 1\)之间的距离,现在要求对于\(k \in [1, n]\),回答选出\(k\)个点,使得所有的两两之间的距离和最大是多少
思路:
显然是两边轮着选,然后找规律统计下答案即可。
K. Counting Failures on a Trie
题意:
给出一个\(Trie\),然后定义一种新的匹配规则:
- 一直在\(Trie\)上匹配,如果失配了,那么跳过这个字符并且从\(Trie\)的根开始匹配,并且失配次数\(+1\)。
- 那么每次匹配会得到失配次数,以及最终在\(Trie\)上匹配的末节点
现在给出一个字符串\(S\),每次询问一段子串\(S[l, r]\)的失配次数以及最后匹配的末节点。
思路:
先将\(Trie\)的每个前缀都\(Hash\)然后将节点作为第二关键字存入\(map\)。
然后对于字符串\(S\),处理一个倍增数组\(f[i][j]\)表示从\(i\)开始匹配\(2^j\)次最远能匹配到哪里。
然后对于每次询问,以\(l\)作为起点进行倍增即可找到最后一次匹配的开始节点\(nl\)。
那么就可以得到失配次数,那么最后的结点就是\(S[nl, r]\)这一段的\(Hash\)值在\(mp\)上的第二关键字。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号