Manthan, Codefest 19
Contest Info
[Practice Link](https://codeforces.com/contest/1208)
| Solved | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| 6/8 | O | O | Ø | O | O | Ø | - | - |
- O 在比赛中通过
- Ø 赛后通过
- ! 尝试了但是失败了
- - 没有尝试
Solutions
A. XORinacci
题意：
\(f(0) = 1, f(1) = b, f(n) = f(n - 1) \oplus f(n - 2)\)，求\(f(n)\)。
思路：
循环节为\(3\)。
B. Uniqueness
题意：
给出一个序列\(a_i\)，可以删去连续的一段，使得剩下的数是互不相同的。
求删除的那一段的最小长度。
思路：
枚举左端点，那么一个右端点可行，当且仅当左端点左边的数是互不相同的，右端点右边的数是互不相同的，并且右端点右边的数中没有左端点左边的数。
- 左端点左边的数是互不相同的，右端点右边的数是互不相同的
- 这两个条件可以\(O(n)\)预处理。
- 右端点右边的数中没有左端点左边的数。
- 这个条件可以维护左端点的数中最后一次出现的位置的最大值，那么右端点比这个最大值还大即可。
C. Magic Grid
题意：
构造一个\(n \cdot n\)的矩阵，里面的数为\([0, n^2 - 1]\)的一个排列。
要求每一行以及每一列的异或和相同。
\(n = 4k\).
思路：
对于\(4\)的情况这样构造：
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
发现每一行每一列都是\(0\)。
那么对于\(n = 4k\)的情况，直接划分成若干个\(4 \cdot 4\)的小矩形，这样仿照的画葫芦即可。
D. Restore Permutation
题意：
有一个排列\(p_i\)，现在告诉你\(s_i\)：
要求还原出\(p_i\)。
思路：
显然一个合法的\(s_i\)的序列唯一对应一个\(p_i\)序列，那么我们从最后一个数考虑。
假设最后一个数为\(p_n\)，那么\(s_n = p_n(p_n - 1) / 2\)。
其实本质就是小于\(p_n\)的数都在它前面，他们的和构成了\(s_n\)。
那么确定了最后一个数，那么依次倒着确定\(s_{n - 1}, s_{n - 2}, \cdots\)。
用线段树维护还有哪些数没有出现，以及他们的和。
对于每个\(s_i\)，在线段树上二分即可。
E. Let Them Slide
题意：
有一个\(n \cdot w\)的矩形，每一行有若干个数，并且每一行的数是可以整体移动的，像这样：
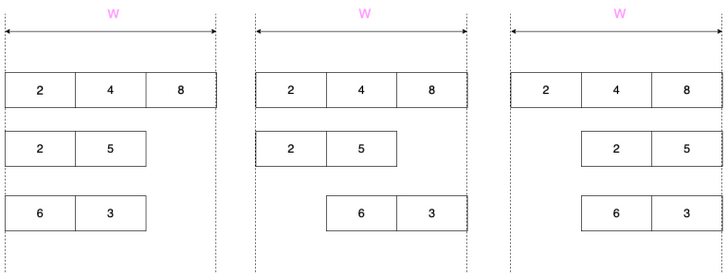
那么现在询问，对于每一列，下面每一行的数如何移动，使得该列的数的和最大，如果没有数那么就是\(0\)。
每一列的询问独立。
思路：
每一行考虑，考虑这一行的哪些数会对哪些列产生贡献。
显然这个每个数产生贡献的范围是连续的，那么用栈贪心维护一下范围即可。
F. Bits And Pieces
题意：
给出一个序列\(a_i\)，询问\(a_i \;|\; (a_j \& a_k)\)这个式子的最大值，其中\(i < j < k\)
思路：
考虑固定\(a_i\)，然后我们只需要关心\(a_i\)那些二进制位上为\(0\)的位，从高位到低位确定。
比如说对于第\(x\)位，那么我们相当于固定了一个前缀，去找\(i < j < k\)是否存在一个\(a_j\)以及一个\(a_k\)，它们都有这样的前缀。
那么直接枚举子集标记前缀即可。 但是这样复杂度不对。
我们可以倒着来，因为我们发现对于一个\((j, k)\)，那么肯定希望\(j, k\)越大越好，那么倒着标记即可，这样标记过了肯定不用再标记了，因为被标记过说明下标肯定大于等于当前的下标。
但是要注意下标等于的情况
