2019 Multi-University Training Contest 8

目录

• Contest Info
• Solutions
  • C - Acesrc and Good Numbers
  • D - Acesrc and Hunting
  • E. Acesrc and String Theory
  • F - Acesrc and Travel
  • H - Andy and Maze
  • I - Calabash and Landlord
  • J - Quailty and CCPC
  • K - Roundgod and Milk Tea

Contest Info

---

[Practice Link](https://cn.vjudge.net/contest/313509#overview)

Solved	A	B	C	D	E	F	G	H	I	J	K
8/11	-	-	O	Ø	Ø	Ø	-	Ø	O	O	O

• O 在比赛中通过
• Ø 赛后通过
• ! 尝试了但是失败了
• - 没有尝试

Solutions

---

C - Acesrc and Good Numbers

题意：
定义\(f(d, n)\)表示小于等于\(n\)的所有数的十进制表示中\(d\)的出现次数。

D - Acesrc and Hunting

题意：
给出一个\(n \cdot m\)的矩形，可以从任何一点出发，要求不重不漏走完所有点，并且保证每一步的步长在\((1, 3)\)以内。
步长是欧几里得距离。

思路：

• \(n < 2\)或者\(m < 3\)的时候无解，但是\(n = 1\)并且\(m = 1\)的时候有解
  我们再考虑前三行类似这样走：
  
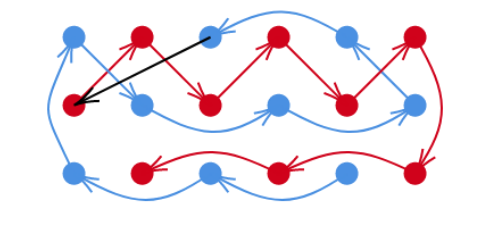
• 如果\(n > m\)，那么直接交换\(n, m\)，然后输出坐标的时候交换输出即可，那么只考虑\(n \leq m\)的情况
• 先从最后一行走起，奇数行走\(2, 4, 6 \cdots\)，偶数行走\(1, 3, 5, \cdots\)然后走到第三行，两行之间交接的步长为\(\sqrt{2}\)
• 然后从第三行的\((3, 1)\)直接走到\((1, 1)\)，步长为\(2\)。
• 然后走到第二行，走\(2, 4, 6, \cdots\)，然后走到第一行，走到\((1, 3)\)之后，走到\((2, 1)\)步长为\(\sqrt{5}\)
• 然后交叉走即可，每一步步长为\(\sqrt{2}\)

E. Acesrc and String Theory

题意：
给出一个字符串\(S\)，找出有多少个子串是\(k\)循环的。

思路：

• 如果一个子串\(t\)的长度为\(len\)，并且它的最小循环节是\(x\)，那么它的贡献是\(len - kx + 1\)
• 那么可以枚举\(x\)，设立\(n / x\)个关键点。
• 考虑相邻的两个关键点\(i\)和\(i + x\)，那么覆盖这两个关键点的循环节是\(x\)的最长字符串是\(s[l, r]\)，其中

\[\begin{eqnarray*} \left\{ \begin{array}{cccc} l &=& i - lcs(i, i + l) + 1\\ r &=& j + lcp(i, i + l) - 1 \end{array} \right. \end{eqnarray*} \]

那么易知，起点在\([l, r - kx + 1]\)这个范围内是可以以它们为顶点有一个循环节是\(x\)的\(k\)循环的子串的
然后我们注意到，对于不同的关键点对，它们的\([l, r]\)是有可能重叠的，但是注意到\(l\)是不递减的，所以可以记录一下上一次区间加的最大的\(lastr\)，将此次的\(l\)与\(lastr + 1\)取Max即可，并且用\(r\)更新\(lastr\)

F - Acesrc and Travel

题意：
有一个\(n\)个点的树，每个点上有两个权值\(a_i, b_i\)，现在\(A、B\)两个人玩游戏，首先由\(A\)选择一个起点开始，然后由\(B\)选择下一个点，然后轮流选择下一个点走哪里。
但是两个人是一起走的，每走到一个点，\(A\)的权值\(W_a\)会加上那个点的\(a_i\)，\(B\)的权值\(W_b\)会加上那个点的\(b_i\)。

• \(A\)想要\(W_a - W_b\)尽量大
• \(B\)想要\(W_a - W_b\)尽量小
  两个人都最优操作，问最后\(W_a - W_b\)是多少？
  注意选择下一个点，能够选择的情况当且仅当下一个点没有被访问过，并且和当前点有一条边相连。
  当没有下一个点可选择时，游戏结束。
  玩家不能选择主动结束游戏。

思路：
反向思考。

• 考虑游戏的行走路径是一条链，并且有一端是叶子结点。
• 那么我们考虑从叶子结点往上走，那么游戏可以结束于任意一个点，但是要保证这一步是先手在操作。
• 也就是说，游戏结束于先手。
• 那么既然游戏结束于先手，先手的目的是要\(W_a - W_b\)尽量大，那么肯定是在所有合法的结束状态中选择\(W_a - W_b\)最大的
• 再考虑怎么转移：
  • 用\(f[u]\)表示从\(u\)的子树转移上来，先手操作可以获得的\(W_a - W_b\)的最大值.
  • 用\(g[u]\)表示从\(u\)的子树转移上来，后手操作可以获得的\(W_a - W_b\)的最小值
  • 那么对于\(f[u]\)的转移，显然是选择它所有儿子\(v\)中\(g[v]\)最小的，因为下一步是后手选择。
• 然后换根\(DP\)即可。
• 这里的换根\(DP\)需要想清楚，但是套路还是一样的。

H - Andy and Maze

题意：
给出\(n\)个点，\(m\)条边的无向图，问寻找一条\(k\)个点的简单路径，使得路径长度和最大。

思路一：
直接爆搜，然后加入一个剪枝即可。

• 如果剩下的边数乘上边权最大的边加上当前的值比已有答案小，那么剩下的路不必走了。
• 不知道是这条剪枝太强，还是数据水，，跑的好快。

思路二：
考虑给每个点随机染色，假设这条路径上的每个点的颜色都不同。
那么有一个\(DP\)，用\(f[u][S]\)表示以点\(u\)结尾，路径上的已用颜色的二进制状态为\(S\)的最大权值和是多少。
那么有转移：

\[\begin{eqnarray*} f(v, S) = max_{u, v \in E, C(u) \in S} f(u, S / \{C(u)\}) + w_{uv} \end{eqnarray*} \]

那么转移的复杂度是\(O(m2^k)\)。
再考虑在最优路径上所有点的颜色都是不同的概率是\(\frac{k!}{k^k}\)，那么我们将这个过程迭代\(\frac{k^k}{k!}\)，那么得到最优解的概率是很高的。

I - Calabash and Landlord

题意：
给出两个矩形，问两个矩形将无限大的平面划分成多少个区域？

思路：
离散化后在\(5 \cdot 5\)的范围内，暴力用并查集合并即可。

J - Quailty and CCPC

签到。

K - Roundgod and Milk Tea

题意：
有\(n\)个班级，每个班级有\(a_i\)个学生，产出\(b_i\)杯牛奶，班级内的学生不能喝自己班级产出的牛奶。
问最多有多少个学生至少能喝上一杯牛奶？

思路：

• 学生和牛奶形成一个二分图。
• 考虑Hall's marriage theorem， 对于一个二分图\((U + V, E)\)来说，其最大匹配为：

\[\begin{eqnarray*} |M| = |U| - max_{S \in U}(|S| - |N(S)|) \end{eqnarray*} \]

其中\(N(S)\)表示的是\(S\)这个点集中连向对面的边数，我们考虑所有\(S'\)可能的情况，有三种：
- \(S' = \empty\)，那么\(N(S) = 0\)，有\(|M| = |U|\)
- \(S'\)中的所有点都来自同一个班级，那么显然将这个点集扩展成那个班级的所有学生，\(N(s)\)没有变。并且\((|S| - |N(s)|)\)变大。
- \(S'\)中的点有来自不同的班级，那么显然\(|N(S)|\)是\(|V|\)，所以\(|M| = |V|\)
分别枚举，然后取最小值即可。