Codeforces Round #573 (Div. 1)

Contest Info
Solutions

Contest Info

[Practice Link](https://codeforces.com/contest/1190)

Solved	A	B	C	D	E	F
4/6	O	O	O	O	-	-

O 在比赛中通过
Ø 赛后通过
! 尝试了但是失败了
- 没有尝试

Solutions

A. Tokitsukaze and Discard Items

题意：
有一个长度为\(n\)的序列，每\(k\)个为一段，有\(m\)个特殊位置需要取走，一段一段过来，每次取走当前段中所有特殊元素，然后后面的元素前移，
继续做这个操作，知道所有特殊元素被取走。
过程类似于这样：

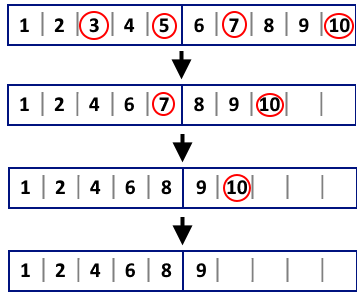
问操作次数。

思路：
显然枚举一遍就可以了，用一个\(lazy\)维护一下当前元素移动后的下标，然后同段的一起取。

代码：

#include <bits/stdc++.h>
using namespace std;
 
#define N 100010
#define ll long long
ll n, k, a[N];
int m;
 
int main() {
	while (scanf("%lld%d%lld", &n, &m, &k) != EOF) {
		for (int i = 1; i <= m; ++i) scanf("%lld", a + i);
		ll lazy = 0;
		int res = 1, tot = 1;
		for (int i = 2; i <= m; ++i) {
			if ((a[i] - lazy - 1) / k != (a[i - 1] - lazy - 1) / k) {
				++res;
				lazy += tot; 
				tot = 1;
			} else {
				++tot;
			}
		}
		printf("%d\n", res);
	}
	return 0;
}

B. Tokitsukaze, CSL and Stone Game

题意：
有\(n\)堆石头，每次只能从一堆中取走一个。
失败条件：

当前没有石头可取。
取走一颗石头后，存在两堆石头个数相同
如果开始的时候有两堆石头相同是没有关系的，只有操作之后还有两堆石头相同才会失败。

思路：

显然取完后最后的石头个数会是从\(0\)开始的依次递增数列,那么可以取的石头个数是固定的。
如果刚开始有两堆及以上为空，那么先手必败
如果有且只有两堆石头个数相同，假设个数为\(x\)，并且也存在\(x - 1\)这堆石头，那么先手必败。
如果刚开始有两堆以上石头个数相同或者又若干个两堆数量相同的石头，那么先手必败。

其实就是个分类讨论题。

代码：

#include <bits/stdc++.h>
using namespace std;
 
#define N 100010
#define ll long long
#define fi first
#define se second
int n, a[N];
ll sum, tot;
map <int, int> mp;
bool ok() {
	mp.clear();
	for (int i = 1; i <= n; ++i) {
		++mp[a[i]];
		if (mp[a[i]] > 2) return 0;
	}
	int cnt = 0;
	for (auto it : mp) {
		if (it.se == 2) {
			++cnt;
		}
	}
	if (cnt == 1) {
		for (auto it : mp) {
			if (it.se == 2) {
				if (it.fi == 0 || mp.find(it.fi - 1) != mp.end()) {
					return 0;
				}
			}
		}
	}
	return cnt <= 1;
}
 
int main() {
	char *fi = "sjfnb";
	char *se = "cslnb";
	while (scanf("%d", &n) != EOF) {
		sum = 0, tot = 0;
		for (int i = 1; i <= n; ++i) {
			scanf("%d", a + i);
			sum += a[i];
			tot += i - 1;
		}
		if (sum == 0 || !ok()) {
			puts(se);
		} else {
			ll res = sum - tot;
			puts(res & 1 ? fi : se);
		}
	}
	return 0;
}

C. Tokitsukaze and Duel

题意：
有一个\(01\)串，每次可以选择连续的\(k\)个，全都变成\(0\)或者全都变成\(1\),两个人轮流行动，谁先把这个串变成全\(0\)或者变成全\(1\)，那么谁胜利，或者判定是否是平局。

思路：
考虑一个先手必胜的情况，即它可以通过第一步操作就把该串变成全\(0\)或者全\(1\)，那么先手必胜。
考虑一个先手必败的情况，即先手第一步无论怎么操作，后手都能在第二步将该串变成全\(0\)或者全\(1\)，那么先手必败。
那么除了这两种情况，接下来的什么情况呢？是平局。
可以这么考虑，如果刚开始的情况不是先手必胜的，那么先手肯定想让局势走向平局，也就是说它的这一步操作不会达到先手必败的状态。
既然不会到达先手必败的状态，那么对手面对的也是同样一个局面，它也会让局势走向平局。
我口胡的。。

代码：

#include <bits/stdc++.h>
using namespace std;
 
#define N 100010
int n, k;
char s[N];
int sum[N];
 
bool ok1() {
	if (n == k) return 1;
	for (int i = 1; i + k - 1 <= n; ++i) {
		int l = i, r = i + k - 1;
		int lenL = l - 1, lenR = n - r;
		int L = sum[l - 1];
		int R = sum[n] - sum[r];
		if (l == 1 && (R == 0 || R == lenR)) return 1;
		if (r == n && (L == 0 || L == lenL)) return 1;
		if ((lenL == L && lenR == R) || (L == 0 && R == 0)) return 1;
	}
	return 0;
}
 
bool ok2() {
	if (k < (n + 1) / 2) return 1; 
	for (int i = 2; i + k - 1 < n; ++i) {
		int l = i, r = i + k - 1;
		int lenL = l - 1, lenR = n - r;
		int L = sum[l -1];
		int R = sum[n] - sum[r];
		if ((L && L != lenL) || (R && R != lenR)) return 1;
	}
	return 0;
}
 
int main() {
	char *fi = "tokitsukaze";
	char *se = "quailty";
	char *draw = "once again";
	while (scanf("%d%d", &n, &k) != EOF) {
		scanf("%s", s + 1);
		sum[0] = 0;
		for (int i = 1; i <= n; ++i) {
			sum[i] = sum[i - 1] - '0' + s[i];
		}
		if (ok1()) {
			puts(fi);
		} else if (ok2()){
			puts(draw); 
		} else {
			puts(se);
		}
	}
	return 0;
}

D. Tokitsukaze and Strange Rectangle

题意：
在二维平面的第一象限中，有若干个点，每次用一个开口向上的容器包含一些点，问包含的点的集合的种类有多少个。
容器类似于这样：

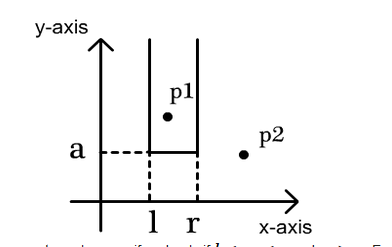
思路：
考虑从上到下，从左到右，枚举每个点。
考虑容器要包含这个点，但是不包含在这个\(y\)轴上的下一个点的方案数。但是可以包含左上角其他所有点的方案数。
其实当容器开口向上的时候，我们只需要在乎某个\(x\)上有没有点，而不需要关系它的\(y\)在哪里，只要它的\(y\)大于等于当前这个点的\(y\)就可以了。
那么假设这个点左边有\(a\)个点，右边有\(b\)个点，那么方案数就是\((a + 1)(b + 1)\)。

代码：

#include <bits/stdc++.h>
using namespace std;
 
#define ll long long
#define N 400010
int n, m, b[N], c[N];
vector <vector<int>> vec;
struct node {
	int x, y;
	node() {}
	void scan() {
		scanf("%d%d", &x, &y);
		b[++b[0]] = x;
		c[++c[0]] = y;
	}
	bool operator < (const node &other) const {
		return x < other.x;  
	}
}a[N];
void Hash() {
	sort(b + 1, b + 1 + b[0]);
	sort(c + 1, c + 1 + c[0]);
	b[0] = unique(b + 1, b + 1 + b[0]) - b - 1;
	c[0] = unique(c + 1, c + 1 + c[0]) - c - 1;
	for (int i = 1; i <= n; ++i) {
		a[i].x = lower_bound(b + 1, b + 1 + b[0], a[i].x) - b;
		a[i].y = lower_bound(c + 1, c + 1 + c[0], a[i].y) - c;
	}
}
struct SEG {
	int a[N << 2];
	void init() {
		memset(a, 0, sizeof a);
	}
	void update(int id, int l, int r, int pos, int v) {
		if (l == r) {
			a[id] = v;
			return;
		}
		int mid = (l + r) >> 1;
		if (pos <= mid) update(id << 1, l, mid, pos, v);
		else update(id << 1 | 1, mid + 1, r, pos, v);
		a[id] = a[id << 1] + a[id << 1 | 1];
	}
	int query(int id, int l, int r, int ql, int qr) {
		if (ql > qr) return 0;
		if (l >= ql && r <= qr) {
			return a[id];
		}
		int mid = (l + r) >> 1;
		int res = 0;
		if (ql <= mid) res += query(id << 1, l, mid, ql, qr);
		if (qr > mid) res += query(id << 1 | 1, mid + 1, r, ql, qr);
		return res;
	}
}seg;
 
int main() {
	while (scanf("%d", &n) != EOF) {
		b[0] = 0; c[0] = 0;
		for (int i = 1; i <= n; ++i) {
			a[i].scan();
		}
		Hash();
		sort(a + 1, a + 1 + n); 
		vec.clear();
		vec.resize(c[0] + 1); 
		for (int i = 1; i <= n; ++i) {
			vec[a[i].y].push_back(a[i].x);
		}
		m = b[0];
		seg.init();
		ll res = 0;
		for (int i = c[0]; i >= 1; --i) {
			if (!vec[i].empty()) {
				for (int j = 0, sze = (int)vec[i].size(); j < sze; ++j) {
					ll L = seg.query(1, 1, m, 1, vec[i][j] - 1);
					ll R = seg.query(1, 1, m, vec[i][j] + 1, (j < sze - 1 ? vec[i][j + 1] - 1 : m));
					res += (L + 1) * (R + 1);
					seg.update(1, 1, m, vec[i][j], 1);
				}			
			}
		}
		printf("%lld\n", res);
	}
	return 0;
}

posted @ 2019-07-13 09:41 Dup4 阅读(270) 评论(0) 编辑收藏举报

刷新页面返回顶部

Dup4.Blog