阻抗模型
在电路计算中引入复数,将电路计算求解变为复阻抗模型下的“欧姆定律”
适合RLC电路正弦稳态分析
正弦稳态
RLC电路在同频率正弦输入下的稳态响应也为正弦
基本电路元件的阻抗

流入元件的电流为I,元件两端的电压为V,元件阻抗为Z
在电机工程及相关领域,j为虚数单位,j2=-1(数学中用i表示)
电路
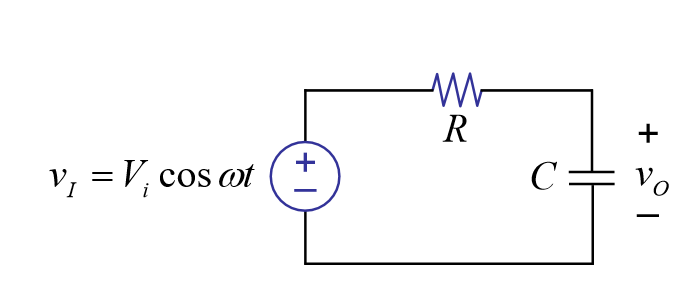
设输入:vI=Vi·cosωt=Re[ Vi·ejωt ]
稳态输出(响应):vo=Re[ Vp·ejwt ]=Re[ |Vp|·ej∠Vp· ejwt]=|Vp|·cos(ωt+∠Vp)
求出Vp即得到响应
阻抗模型
通交流电后,电容电阻电感会对电路产生阻碍作用,阻碍的大小称为阻抗。分析时可将它们用对应的阻抗模型进行替代。就像电阻将欧姆定律延伸至交流电路领域,其它直流电路分析的结果,例如电压分配(voltage division)、电流分配(current division)、戴维宁定理、诺顿定理等等,都可以延伸至交流电路领域,只需要将电阻更换为阻抗就行了。
在阻抗模型中,将原电路各元件以阻抗形式替换,得到下图(Vc即Vp)
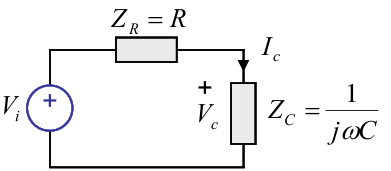
原理同两电阻串联分压,得到

将Zc、ZR带入,得

整理可得

得到Vc即可依照vo=|Vp|·cos(ωt+∠Vp)得到电路稳态响应。
参考:
作者:Dumblidor
转载请注明出处
2017.1.26



