第一节、方程组的几何解释
一、线性方程组
啥是方程组？把一堆方程放在一起就是方程组。比如：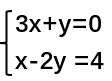 
是方程组，
也是方程组。相关概念就不多叙述了，如有需要请自行百度。
另外说说线性，所谓线性，就是指量与量之间按比例、成直线的关系。换句话说，线性代数里研究的所有变量都是一次的，所以千万不要在这里脑抽问遇到x2+y=1咋办啊之类的问题呦。至于线性方程的其他性质，自行百度。
二、方程组的矩阵表示
（1）先以两方程两未知数的举例：
现在有一个方程组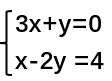
我们把变量的系数单独拿出，得到这样的一个矩阵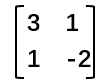 
（没错，介货就是矩阵，可以看出它的数字排列和上面方程组的系数是一一对应的），我们管这个矩阵叫做系数矩阵，用A表示。
然后，我们用两个未知数组成一个列向量
（为啥叫向量呢？因为人家就一列啊），用x表示。
最后，再写出一个列向量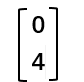
，没错，这货是由两个方程的得数组成的，用b表示。
经过上面的步骤，就可以得到方程组的矩阵表示了，让我们对比着看一下
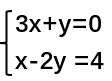
Ax=b
（2）同理，三方程三未知数（以及其他情况）的方程组也可以用相同的方法进行表示。
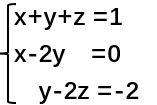
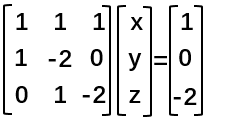
Ax=b
三、方程组的几何解释
（1）先以两方程两未知数进行举例：
首先，瞎编一个方程组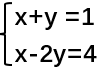 
（为了方便绘图，这里的方程组和之前所用的不同）
第一步，我们作该方程组的行图像。
一次拿一行（一个方程），在xy坐标系上做出方程的图像。
如图可知，红色的是x+y=1的图像，绿色的是x-2y=4的图像，交点坐标(2,-1)，so，x=2,y=-1为方程组的解
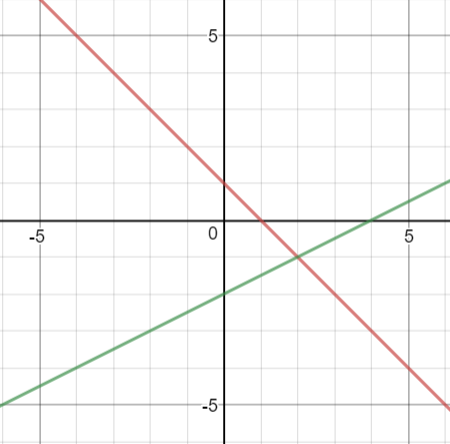
行图像大家都非常熟悉了，在此不做过多介绍
第二步，我们看一下列图像
首先，我们写出方程组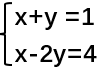 ，顺便写出矩阵形式
然后，我们按列将系数拿出，写成如下形式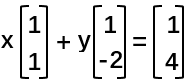
（在此处，我们实际是将系数矩阵A的每一列作为一个向量拿出）。
现在，我们的任务是寻找一对合适的xy，使得x倍的向量
与y倍的向量
能组合成向量
（线性组合）。
三个向量图形如下
在前面我们已经求出方程组的解为x=2,y=-1，让我们将其带入，看看会发生什么
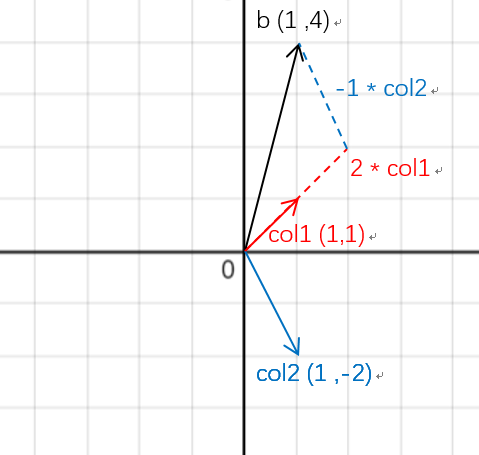
带入后发现，所得到的向量就是向量b。
让我们分析一下计算过程，将2倍的向量与-1倍的向量进行线性组合，上方2*1+(-1)*1=1、下方2*1+(-1)*(-2)=4，由此得到。
事实上，若两个分量（即我们提取出来的两个列向量）不共线，他们的线性组合可以构成xy坐标系内的任意一个向量。这个以后再讨论
（2）两方程两未知数的说完了，让我们看看三方程三未知数的情况
先召唤一个方程组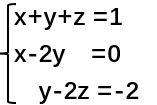
第一步，作该方程组的行图像
两未知数的方程作图是一条直线，而三未知数的方程作图是一个平面，理论上（有解时）三个平面会相交于一点，该点坐标即为方程组的解。
如图，x+y+z=1, x-2y=0 , y-2z=-2 。（画风鬼畜，见谅）
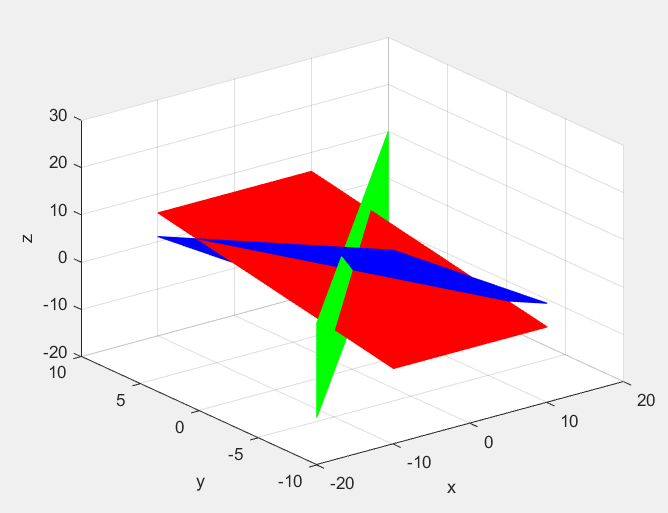
这里可以看出，用行图像解三元的方程组并不简单，那么列图像表现又如何呢？
第二步，作方程组的列图像
话不多说
我们的目的是用x倍的
加上y倍的
，加上z倍的
构成
。
这里就不画图像了，大家可以看出（一般书里用的是“显然”），只需要让x=0,y=0,z=1就可以得到我们想要的向量
，相比于行图像，列图像在这里显得十分简洁方便
对于变量更多的方程组，我们不可能画出他们的图像，但借助列向量我们却可以对它们进行直观的认识
四、矩阵乘以向量计算
这里简单介绍下矩阵和向量相乘的计算，完整矩阵相乘版以后会讲
首先召唤一个矩阵和一个向量，比如 
，它们两个相乘可以看作取四个第一列和一个第二列然后相加，即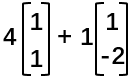
，也就是
。换句话说，矩阵乘以向量的结果是矩阵列的线性组合。
当然，还有另外一种方法，矩阵相乘的解矩阵中的第i行第j个列的数是第一个矩阵的第i行和第二个矩阵的第j列点乘的结果。
