B1277 [HNOI2002]Tinux系统 树形dp
这个题bzoj上没有图，luogu上样例有问题。。。其实这个题代码不难，但是思考起来还是有一定难度的，其实这些题的重点都在于思考。我就不写了，洛谷上唯一的题解写的挺好，大家可以看一看。
题干：
在dos系统诞生以前，美国曾研究出一种类似的操作系统，名为Tinux系统。但由于硬件设施的制约，Tinux系统有许多的缺点。下面就对Tinux系统作一个简单的介绍：
Tinux系统是Tiger博士为美国军方研制开发的一种操作系统，该系统对文件的存储方式类似于dos系统，像一棵树一样，每一个叶子节点表示一个文件，每一个非叶子节点表示一个目录。其中定义i级子目录表示从根目录开始访问，一直访问到该子目录（不包括该子目录）需要访问的目录的个数为i的目录，所以根目录下的目录为一级子目录，其他的目录以此类推。但是在同一子目录下，受到硬件的制约Tinux系统最多只能够存储k个文件或子目录，也就是说这棵树里面的每一个非叶子节点最多只有k个子节点。这样就导致在文件数量较多的情况下，访问存储在该系统当中的文件A，往往要先访问一系列的子目录，我们称这些子目录为文件A的上级目录。例如下面这一个例子：
Root A1
A2
A3
A4
A4A1
A4A2
A4A2A1
A4A2A2
A4A3
当我们要访问文件A4A2A1时就必须先访问它的上级目录：一级子目录A4和二级子目录A4A2。
Tinux系统在存储文件时，给每一个子目录都分配了k个指针，分别指向存放在该目录下的每一个文件和每一个目录，因此对文件的访问实质上就是对指针的访问。但是由于硬件原因，这k个指针不尽相同，因此访问它们的时间也不同，访问第i个指针所耗费的时间为 。但是对于两个不同的子目录（不管它们各自属于哪一级目录）而言它们各自所拥有的k个指针是相同的。
Tinux系统最大的缺点是访问一个目录时，必须把该目录下所有的文件读入到内存当中来，这些文件包括在其各级子目录当中的文件，例如上面那一个例子，访问A4那一个目录，就必须把A4A1，A4A2A1，A4A2A2，A4A3这四个文件都读入到内存当中来，访问一个目录所需要的时间为 （x表示该目录及其各级子目录下文件的个数， 表示指向该目录的指针的访问时间）。因此根据上面介绍的访问方法，单独访问一个文件所需要的总时间为访问其所有上级目录（不包括根目录）所需要的时间与访问指向该文件的指针所需要的时间的和，例如上面那一个例子，访问文件A4A2A1需要的时间=访问目录A4的时间+访问目录A4A2的时间+访问指向文件A4A2A1的指针需要的时间。
现在，tiger博士准备将n个文件存储到一个空的Tinux系统当中，希望你帮助他设计一个程序找到一种最优的存储方法，使得单独访问这n个文件所需要的时间总和最小。
输入输出格式
输入格式：
输入由文件”system.in”读入。
文件的第一行为两个正整数 ， ，接下来的k行每行有一个正整数 。
输出格式：
输出到文件”system.out”，输出文件仅有一个正整数，表示在最优存储方案下，单独访问这n个文件所需要的时间总和。（结果小于2的31次方 ）
输入输出样例
说明
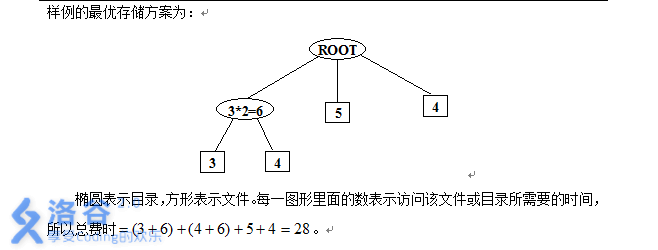
代码：
#include<iostream> #include<cstdio> #include<cmath> #include<ctime> #include<queue> #include<algorithm> #include<cstring> using namespace std; #define duke(i,a,n) for(int i = a;i <= n;i++) #define lv(i,a,n) for(int i = a;i >= n;i--) #define clean(a) memset(a,0,sizeof(a)) const int INF = 1 << 30; typedef long long ll; typedef double db; template <class T> void read(T &x) { char c; bool op = 0; while(c = getchar(), c < '0' || c > '9') if(c == '-') op = 1; x = c - '0'; while(c = getchar(), c >= '0' && c <= '9') x = x * 10 + c - '0'; if(op) x = -x; } template <class T> void write(T x) { if(x < 0) putchar('-'), x = -x; if(x >= 10) write(x / 10); putchar('0' + x % 10); } int f[1700][1700]; int n,k,p[1700]; int MIN(int x,int y) { if(!x) return y; else return min(x,y); } int dp(int x,int y,int l) { if(x == 1) { f[x][y] = p[y]; return f[x][y]; } if(y == k) { f[x][y] = p[y] * x * x + dp(x,1,x - 1); return f[x][y]; } int tmp = k - y + 1; if(tmp * l < x) return INF; if(f[x][y]) return f[x][y]; tmp = (x - 1) / tmp + 1; duke(i,tmp,l) { if(i == 1) f[x][y] = p[y] + dp(x - 1,y + 1,x - 2); else f[x][y] = MIN(f[x][y],dp(x - i,y + 1,x - i - 1) + dp(i,1,i - 1) + p[y] * i * i); } return f[x][y]; } int main() { read(n);read(k); duke(i,1,k) read(p[i]); sort(p + 1,p + k + 1); printf("%d\n",dp(n,1,n - 1)); return 0; }
