深入理解计算机系统（一） 二进制数字系统（bit，整数，浮点数详解）
前言
csapp（黑皮书之一）是计算机底层的百科全书，是世界一流学校的教材。作者是CMU计科院长，至今为止，CMU计科仍在世界顶尖。
此书涵盖知识面非常广，并且讲的很透彻，回答了我之前疑惑的“为什么这么设计”的问题。
链接：
深入理解计算机系统（一） 二进制数字系统（bit，整数，浮点数详解）
背景
在人类历史发展和社会生活中，数学发挥着不可替代的作用，同时也是学习和研究现代科学技术必不可少的基本工具。
计算机作为电子大脑，必不可少的便是拥有一套数字系统。
使用二进制表示数据
需要一个物理信息来表示数据，可以是温度，或者电压大小等。
出现了两种选择: 1.模拟信号实现的十进制 2.数字信号实现的二进制
出于硬件成本，稳定性等考虑，选取了更为简便的二进制。
二进制数字系统的构成
1. 二进制编码：对bit位进行解释，表示有限集合元素。
二进制编码方式: 无符号编码，补码编码，浮点数编码
2. 运算属性: 满足部分普遍属性,如交换律和结合律。
学习目的
理解可以表示的值的范围和不同运算的属性,很多安全漏洞都是由于计算机运算的微妙细节引起的。
理解编码设计的巧妙和推导过程。
信息存储
用bit位存储
bit位存储的两种方式：字节序
整数表示
无符号编码(无符号整数)
公式：
缺点：不能表示负数。
应用场景： 位运算
补码编码（有符合整数）
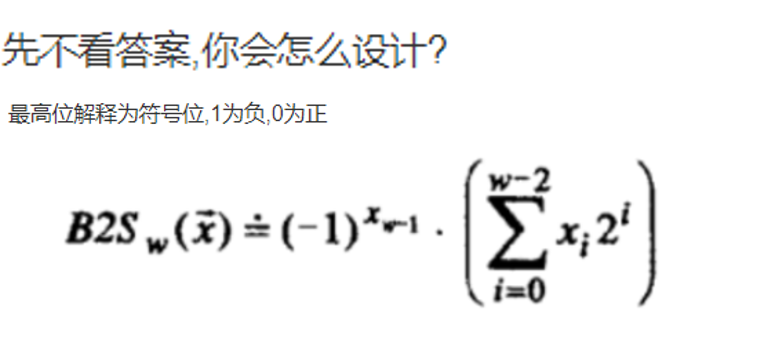
设计缺陷： 1. 表示±0，有歧义
2.与无符号编码的转换复杂(后面运算属性的推导会体现)
公式：
补码优势：
符号位扩展证明：
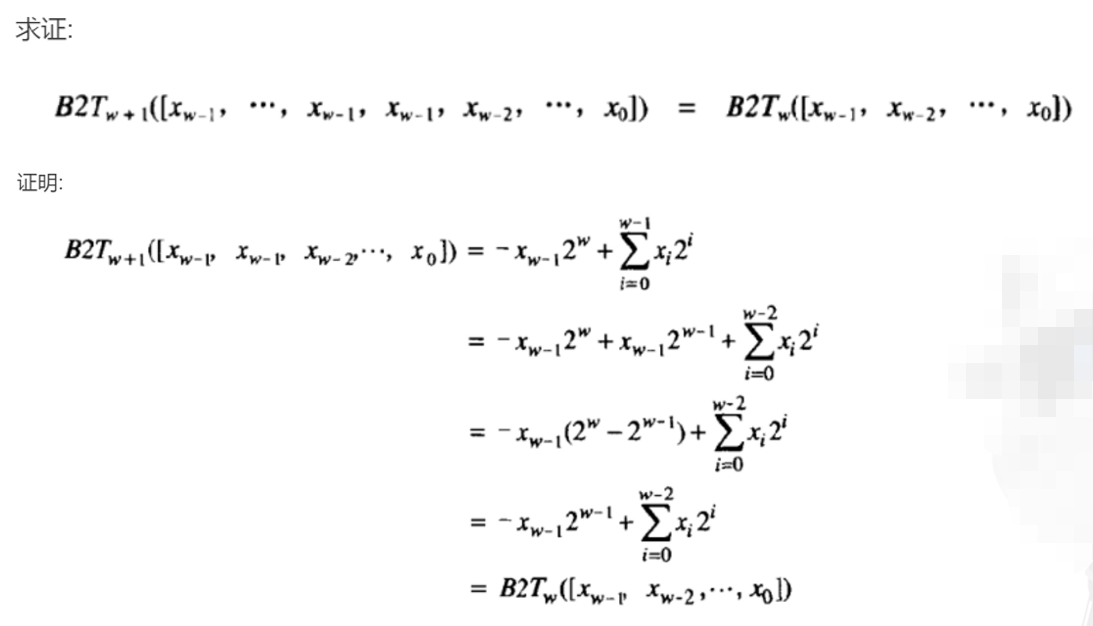
截断证明：
整数运算
正常整数加法模型：
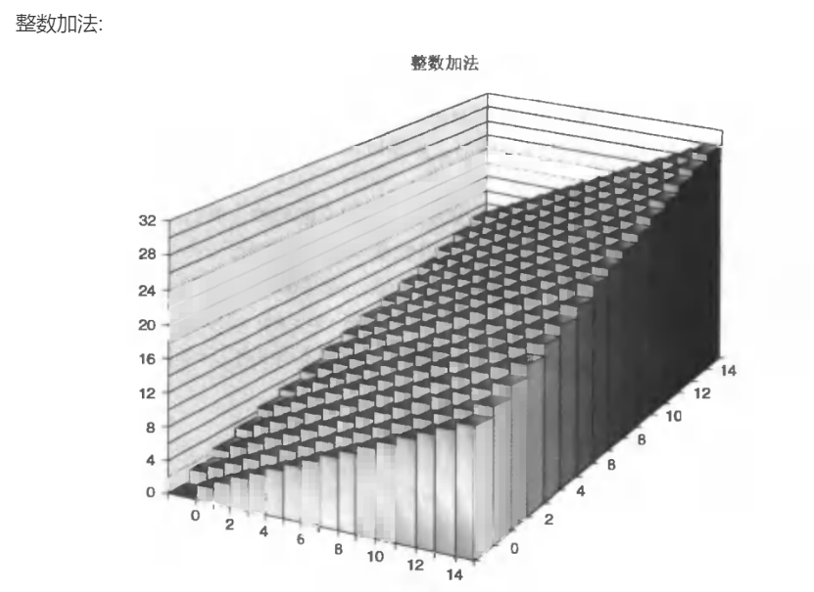
无符号加法
公式:
模型：
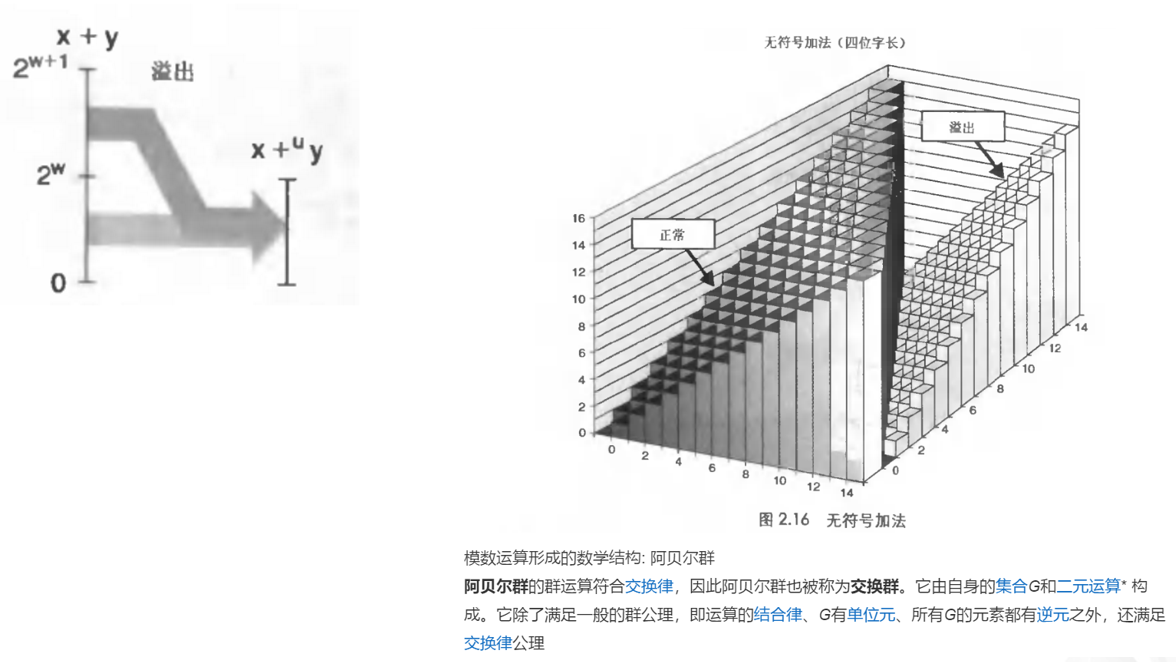
补码加法
公式：
模型：
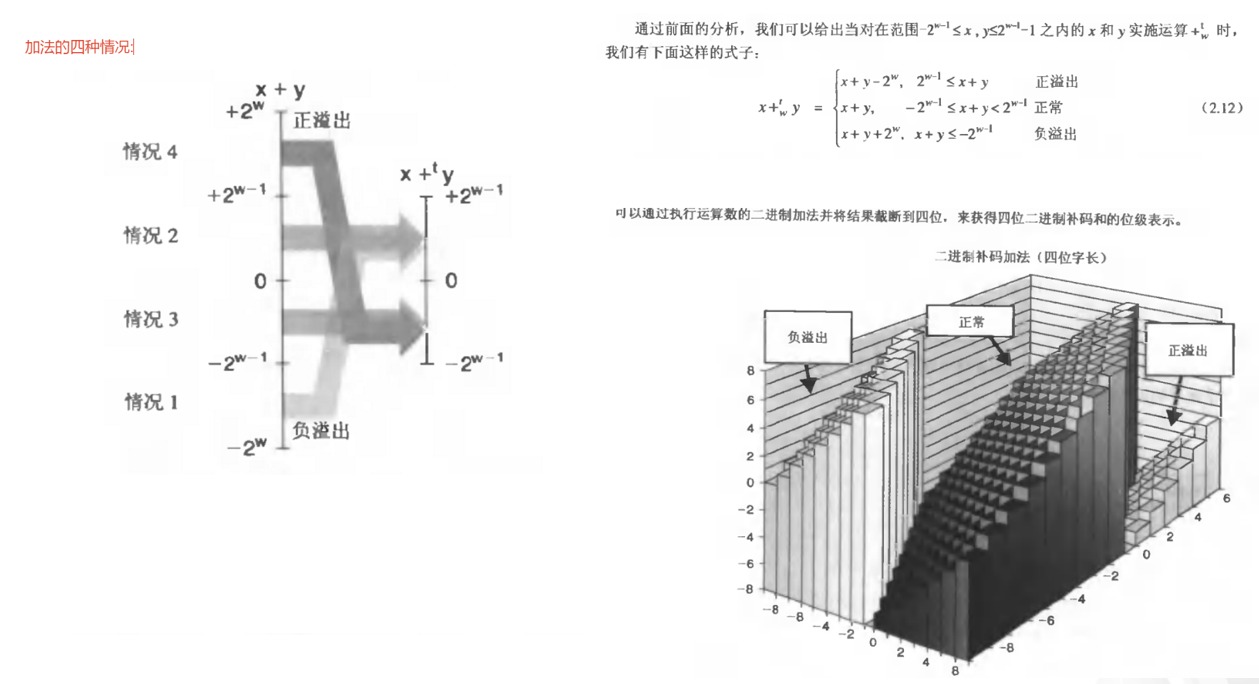
补码逆元：
乘法
与加法类似，都是保留低位的思想，不做赘述。
移位运算
浮点数
因为浮点数本质是二进制小数，为了便于理解，对十进制小数和二进制小数做了对比：
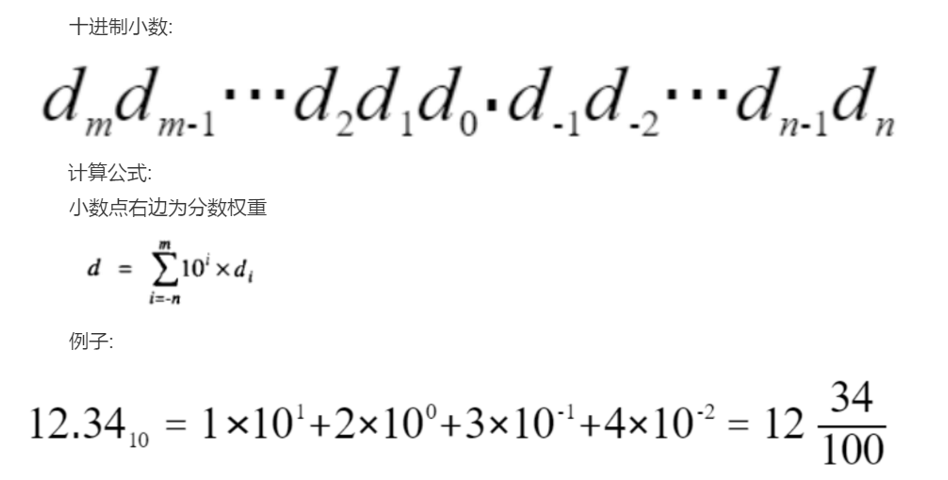
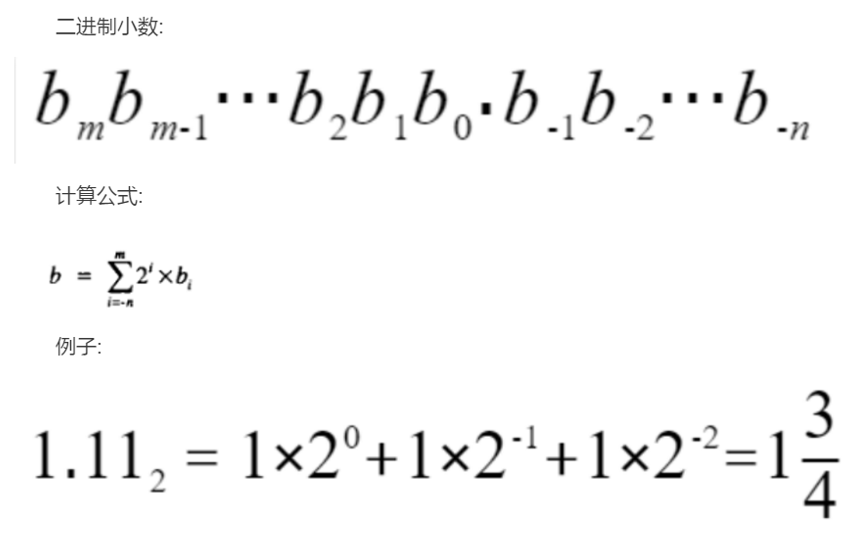
因为编码必须规定长度，所以我们也知道有限小数的局限性：
公式：
为什么叫浮点数？
当小数点右移，能表示更大的数，当小数点左移，能表示更精确的数。这样的设计，会让小数表示的更多，包含了所有的定点数，而小数点的位置，由指数E决定。
内存模型
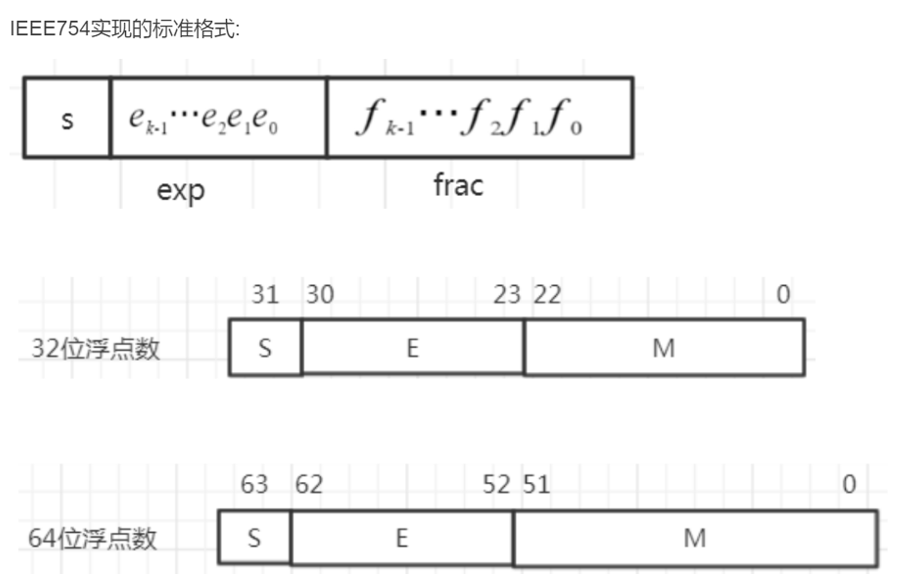
具体实现
模型：
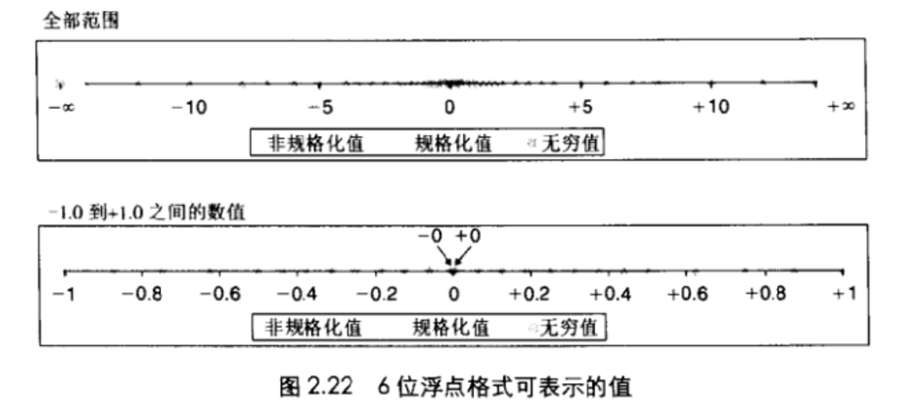
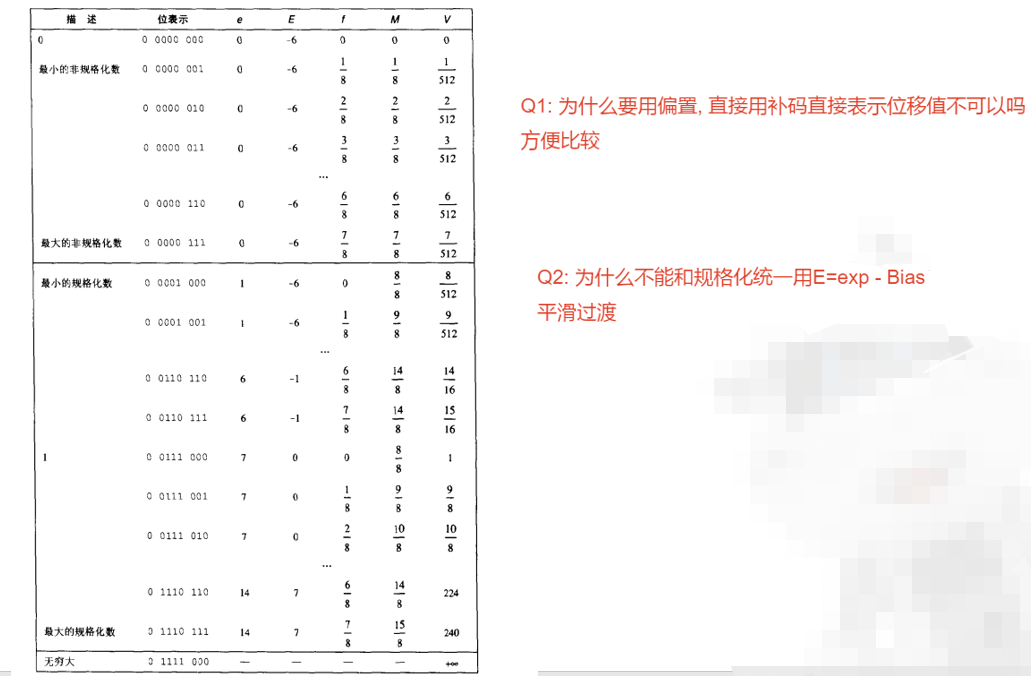
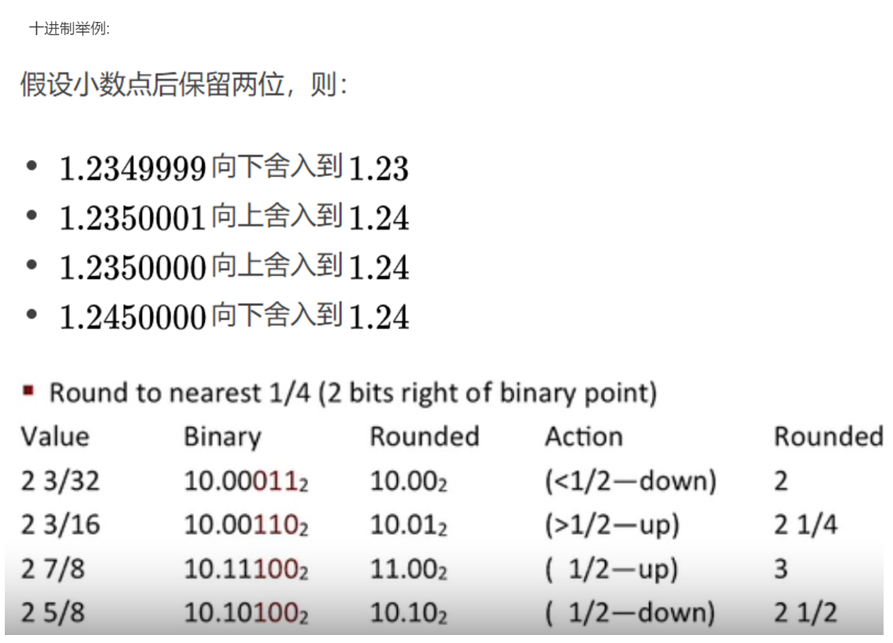
舍入例子
乘法和加法公式
总结
