NOIP 2016 Day2 T1 组合数问题

题意概述

给定组合数公式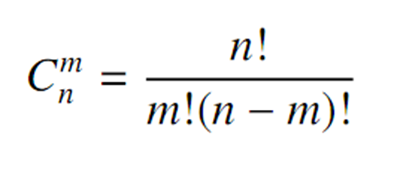

小葱想知道如果给定n, m和k，对于所有的0 <= i <= n, 0 <= j <= min(i, m)有多少对(i, j)满足

是k的倍数。

输入格式

第一行有两个整数t, k，其中t代表该测试点总共有多少组测试数据，k的意义见【问题描述】。

接下来t行每行两个整数n, m，其中n, m的意义见【问题描述】。

输出格式

t行，每行一个整数代表所有的0 <= i <= n, 0 <= j <= min(i, m)有多少对(i, j)满足CijC_i^jC​i​j​​是k的倍数。

样例1

样例输入1

1 2
3 3

样例输出1

1

样例2

样例输入2

2 5
4 5
6 7

样例输出2

0
7

 

 题解

这是一道明显的数论题，那么画一画即可得到组合数的递推式
其实也是可以证明的，但是不在这里赘述了。

那么因为n,m都是小于2000的，并且对于每一个测试点，k是不变的。所以预处理出2000以内的个数，然后根据输入的n,m统计就好了

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
int a[2005][2005], tj[2005][2005];
int n, m, ans, t, k;
int main()
{
    scanf("%d%d",&t,&k);
    memset(a,0,sizeof(a));
    a[1][1] = 1 % k;
    if (a[1][1] == 0) tj[1][1]++;
    for (int j=2; j<=2001; j++)
         for (int q = 1; q <= min(j, 2001); q++)
        {
             if (q == 1) a[j][q] = (a[j-1][q] + 1) % k;
              else a[j][q] = (a[j-1][q] + a[j-1][q-1])%k;
              if (a[j][q] == 0) tj[j][q] = tj[j][q-1]+1; 
            else tj[j][q] = tj[j][q-1];
        }
    for (int i=1; i<=t; i++)
    {
        scanf("%d%d",&n, &m);
        ans = 0;
        for (int j=1; j<=n; j++)
             ans += tj[j][min(m,j)];
        printf("%d\n", ans);
    }
    return 0;      
}