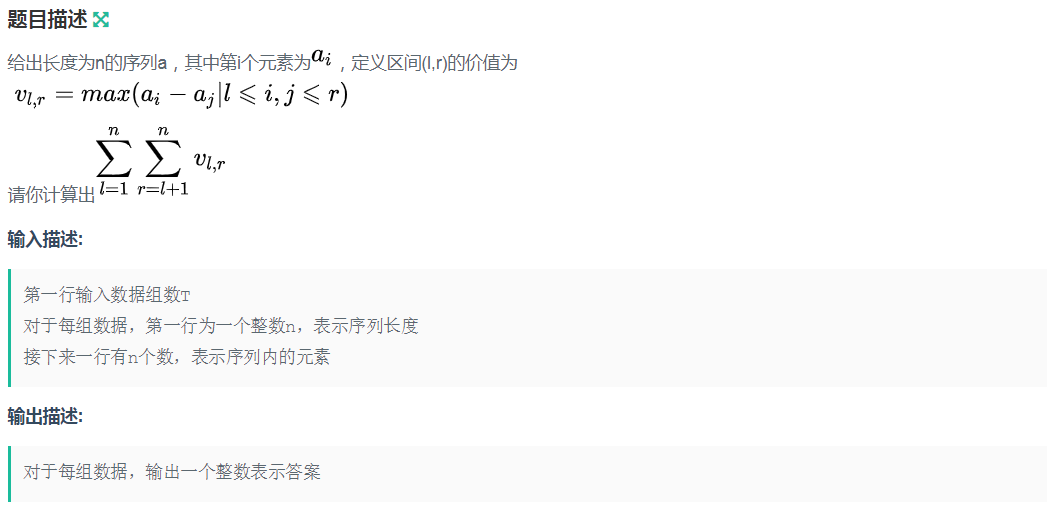
牛客网 牛可乐发红包脱单ACM赛 C题 区区区间间间
【题解】
我想到了两种解法。
一种是扫描线+线段树+单调栈。
另一种方法是O(n)的，比较巧妙。
考虑每个数在哪些区间可以作为最小数。最长的区间就是它向左右走，直到有数字比它小，这个可以用单调栈维护。
那么区间数就是它左边可以走的距离*右边可以走的距离，答案减去这个数字*区间数。
再考虑每个数在哪些区间可以作为最大数。方法是一样的。
那么4次单调栈即可。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define LL unsigned long long 5 #define rg register 6 #define N 200010 7 using namespace std; 8 int T,n,m,top,v[N],l[N],r[N]; 9 struct stack{int num,pos;}st[N]; 10 LL ans,sum[N]; 11 inline LL read(){ 12 LL k=0,f=1; char c=getchar(); 13 while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar(); 14 while('0'<=c&&c<='9')k=k*10+c-'0',c=getchar(); 15 return k*f; 16 } 17 int main(){ 18 T=read(); 19 while(T--){ 20 ans=0; 21 n=read(); 22 for(rg int i=1;i<=n;i++) v[i]=read(); 23 for(rg int i=1;i<=n;i++) sum[i]=sum[i-1]+v[i]; 24 top=0; 25 st[0].pos=0; 26 for(rg int i=1;i<=n;i++){ 27 while(st[top].num>v[i]&&top>0) top--; 28 st[++top].num=v[i]; st[top].pos=i; 29 l[i]=st[top-1].pos+1; 30 // printf("top=%d\n",top); 31 } 32 top=0; 33 st[0].pos=n+1; 34 for(rg int i=n;i;i--){ 35 while(st[top].num>=v[i]&&top>0) top--; 36 st[++top].num=v[i]; st[top].pos=i; 37 r[i]=st[top-1].pos-1; 38 } 39 for(rg int i=1;i<=n;i++) ans-=1ll*(i-l[i]+1)*(r[i]-i+1)*v[i]; 40 // for(rg int i=1;i<=n;i++) printf("%d %d\n",l[i],r[i]); 41 top=0; 42 st[0].pos=0; 43 for(rg int i=1;i<=n;i++){ 44 while(st[top].num<v[i]&&top>0) top--; 45 st[++top].num=v[i]; st[top].pos=i; 46 l[i]=st[top-1].pos+1; 47 } 48 top=0; 49 st[0].pos=n+1; 50 for(rg int i=n;i;i--){ 51 while(st[top].num<=v[i]&&top>0) top--; 52 st[++top].num=v[i]; st[top].pos=i; 53 r[i]=st[top-1].pos-1; 54 } 55 // for(rg int i=1;i<=n;i++) printf("%d %d\n",l[i],r[i]); 56 for(rg int i=1;i<=n;i++) ans+=1ll*(i-l[i]+1)*(r[i]-i+1)*v[i]; 57 printf("%lld\n",ans); 58 } 59 return 0; 60 }
