BZOJ 3251 树上三角形

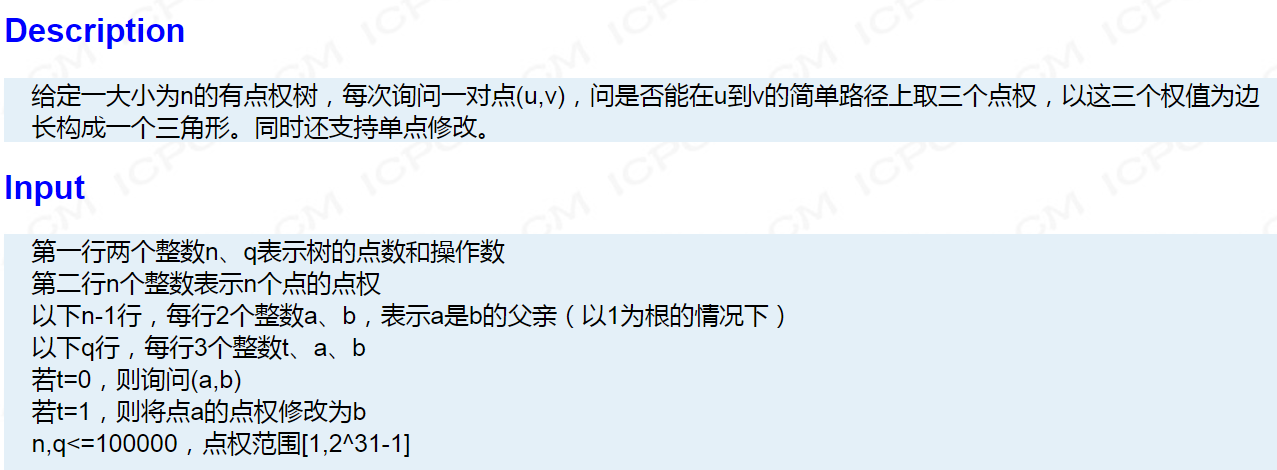
【题解】

　　算是个思维题。。

　　题目数据范围很大，而是否能组成三角形这种信息也无法用数据结构维护，那怎么办呢？

　　我们可以发现，如果想要一个数列任意三项不能组成三角形且各项尽量小，这个数列就是一个斐波那契数列。而本题中点权范围为int范围内，我们可以发现在int范围内斐波那契数列只有46项。

　　

 

　　那么如果给出的链上面的点数大于50项，就一定存在三个点可以组成三角形。如果链上的点数小于50，我们直接排序后判断即可。

　　

#include<cstdio>
#include<algorithm>
#define rg register
#define N 100010
using namespace std;
int n,m,tot,val[N],tmp[N],fa[N],last[N],dep[N];
struct edge{
    int to,pre;
}e[N<<1];
inline int read(){
    int k=0,f=1; char c=getchar();
    while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar();
    while('0'<=c&&c<='9')k=k*10+c-'0',c=getchar();
    return k*f;
}
void dfs(int x){
    for(rg int i=last[x],to;i;i=e[i].pre) 
        dep[to=e[i].to]=dep[x]+1,dfs(to);
}
inline bool query(int x,int y){
    int cnt=0;
    while(cnt<50){
        if(dep[x]<dep[y]) swap(x,y);
        tmp[++cnt]=val[x];
        if(x==y) break; 
        x=fa[x];
    }
    if(cnt>=50) return 1;
    sort(tmp+1,tmp+1+cnt);
    for(rg int i=1;i<=cnt-2;i++) 
        if(tmp[i]>tmp[i+2]-tmp[i+1]) return 1;
    return 0;
}
int main(){
    n=read(); m=read();
    for(rg int i=1;i<=n;i++) val[i]=read();
    for(rg int i=1;i<n;i++){
        int x=read(),y=read();
        e[++tot]=(edge){y,last[x]}; last[x]=tot;
        fa[y]=x;
    }
    dfs(dep[1]=1);
    while(m--){
        int opt=read(),x=read(),y=read();
        if(opt==0) puts(query(x,y)?"Y":"N");
        else val[x]=y;
    }
    return 0;
}