HDU 5217 Brackets
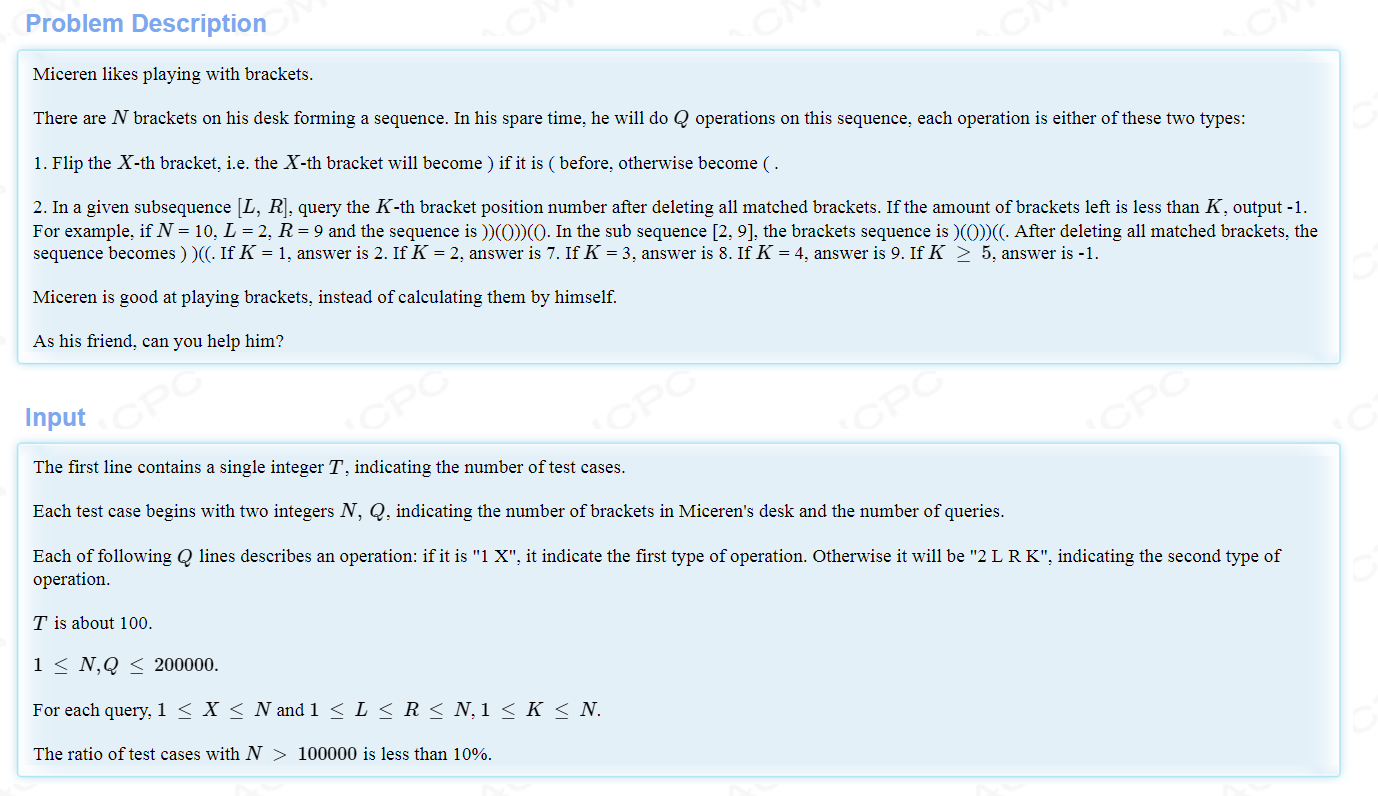
【题意概述】
给出一个有左括号和右括号的序列，左边的左括号和右边的右括号可以合并。现在要求你维护这个序列，支持两种操作：
1，翻转某个位置的括号；
2，查询区间[L,R]合并后第k个括号在原序列中的位置，如果k超过区间合并后的括号总数，输出-1.
【题解】
首先我们可以发现，对于一个区间，合并后的结果一定是若干个右括号、若干个左括号的形式。即))))(((((...
线段树上维护两个标记，区间左边的右括号数量cl、区间右边的左括号数量cr。合并的时候把左区间的cr和右区间的cl抵消一下，然后计算新的cl、cr即可。
这样对于询问，我们可以快速确定它是左括号还是右括号，或者不满足题意输出-1。但我们怎么求第k个左/右括号在原序列中的位置呢？我的做法是询问的时候把经过的各个区间记录一下，逐个区间查找，如果k落在当前区间，就进入线段树进行查找，走到叶子结点就是答案。也可以直接在线段树上查找，不把区间取出来。
1 #include<cstdio> 2 #include<algorithm> 3 #define rg register 4 #define N 200010 5 #define ls (u<<1) 6 #define rs (u<<1|1) 7 using namespace std; 8 int T,n,m,f[N],s[N],cnt,rt; 9 char c[N]; 10 struct tree{ 11 int l,r,cl,cr; 12 }a[N<<2]; 13 struct rec{ 14 int cl,cr; 15 }; 16 inline int read(){ 17 int k=0; char c=getchar(); 18 while(c<'0'||c>'9')c=getchar(); 19 while('0'<=c&&c<='9')k=k*10+c-'0',c=getchar(); 20 return k; 21 } 22 inline void pushup(int u){ 23 a[u].cl=a[ls].cl; a[u].cr=a[rs].cr; 24 int tmp=a[ls].cr-a[rs].cl; 25 if(tmp>0) a[u].cr+=tmp; 26 else a[u].cl-=tmp; 27 } 28 void build(int u,int l,int r){ 29 a[u].l=l; a[u].r=r; a[u].cl=a[u].cr=0; 30 if(l<r){ 31 int mid=(l+r)>>1; 32 build(ls,l,mid); build(rs,mid+1,r); 33 pushup(u); 34 } 35 else{ 36 if(f[l]==0) a[u].cr=1; else a[u].cl=1; 37 } 38 } 39 void update(int u,int pos){ 40 if(a[u].l==a[u].r){ 41 a[u].cl^=1; a[u].cr^=1; return; 42 } 43 int mid=(a[u].l+a[u].r)>>1; 44 if(pos<=mid) update(ls,pos); 45 else update(rs,pos); 46 pushup(u); 47 } 48 rec query(int u,int l,int r){ 49 if(l<=a[u].l&&a[u].r<=r){ 50 s[++cnt]=u; 51 rec tmp; 52 tmp.cl=a[u].cl; tmp.cr=a[u].cr; 53 return tmp; 54 } 55 int mid=(a[u].l+a[u].r)>>1; 56 rec ret,L,R; ret.cl=ret.cr=0; 57 if(l<=mid) ret=L=query(ls,l,r); 58 if(r>mid) ret=R=query(rs,l,r); 59 if(l<=mid&&r>mid){ 60 ret.cl=L.cl; ret.cr=R.cr; 61 int tmp=L.cr-R.cl; 62 if(tmp>0) ret.cr+=tmp; 63 else ret.cl-=tmp; 64 } 65 return ret; 66 } 67 int findl(int u,int k){ 68 if(a[u].l==a[u].r) return a[u].l; 69 if(a[ls].cl>=k) return findl(ls,k); 70 return findl(rs,k-a[ls].cl+a[ls].cr); 71 } 72 int findr(int u,int k){ 73 if(a[u].l==a[u].r) return a[u].l; 74 if(a[rs].cr>=k) return findr(rs,k); 75 return findr(ls,k-a[rs].cr+a[rs].cl); 76 } 77 int main(){ 78 T=read(); 79 while(T--){ 80 n=read(); m=read(); 81 scanf("%s",c+1); 82 for(rg int i=1;i<=n;i++) if(c[i]=='(') f[i]=0; else f[i]=1; 83 build(1,1,n); 84 while(m--){ 85 int opt=read(); 86 if(opt==1){ 87 int x=read(); 88 update(1,x); 89 } 90 else{ 91 int l=read(),r=read(),k=read(); cnt=0; 92 rec tmp=query(1,l,r); 93 if(tmp.cl+tmp.cr<k){ 94 puts("-1"); 95 continue; 96 } 97 if(tmp.cl>=k){ 98 for(rg int i=1;i<=cnt;i++){ 99 if(a[s[i]].cl>=k){ 100 rt=s[i]; break; 101 } 102 else k+=a[s[i]].cr-a[s[i]].cl; 103 } 104 printf("%d\n",findl(rt,k)); 105 } 106 else{ 107 k=tmp.cl+tmp.cr-k+1; 108 for(rg int i=cnt;i;i--){ 109 if(a[s[i]].cr>=k){ 110 rt=s[i]; break; 111 } 112 else k+=a[s[i]].cl-a[s[i]].cr; 113 } 114 printf("%d\n",findr(rt,k)); 115 } 116 } 117 } 118 } 119 return 0; 120 }
