【Python】最小二乘法（线性回归LinearRegression（）和岭回归Ridge（））——东北大学数据挖掘实训一（2）

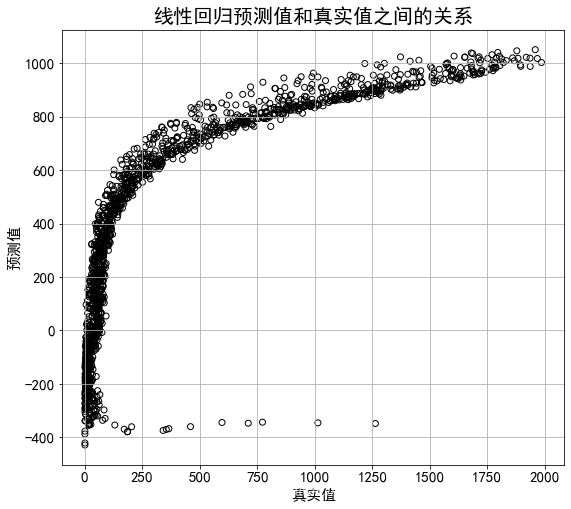
（3）根据分析结果，利用年龄、年份和对数生存人口数（L_male_exp）这3个变量与死亡人数（Male_death）之间的关系，利用普通最小二乘线性模型进行模型拟合，并进行预测；将观测值与拟合值，进行图形展示（以样本的观测值做为x轴，拟合值作为y轴绘制散点图）

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.linear_model import Ridge,RidgeCV   # Ridge岭回归,RidgeCV带有广义交叉验证的岭回归
from sklearn.metrics import r2_score

df=pd.read_csv("C:\\Users\\zzh\\Desktop\\dataMiningExperment\\第一次数据挖掘实训\\death rate.csv")

df.head()

	Year	Age	Female_Exp	Male_Exp	q_female	q_male	Female_death	Male_death	L_female_exp	L_male_exp
0	1951	0.0	53684.67	57059.14	0.018497	0.024273	993.005341	1384.996505	10.890883	10.951844
1	1951	1.0	56056.20	59379.55	0.001944	0.002021	108.973253	120.006071	10.934110	10.991705
2	1951	2.0	59026.83	61855.13	0.001186	0.001455	70.005820	89.999214	10.985747	11.032550
3	1951	3.0	60794.23	63620.28	0.000888	0.000959	53.985276	61.011849	11.015250	11.060688
4	1951	4.0	61980.55	65167.32	0.000484	0.001013	29.998586	66.014495	11.034576	11.084713

df=df.dropna() #删除有缺失值的行
df=df[(df.q_male>0) & (df.q_male<=1)]   #取出死亡率在0<q<=1范围内的数据

将数据集进行划分，训练集与测试集的比例为3:1（数据的前3/4做为训练集，后1/4做为测试集）

x=df[['Year','Age','L_male_exp']].values
y=df[['Male_death']].values

x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25,random_state=2) # 划分训练集和测试集

x_train.shape[0]/df.shape[0]

0.75

对训练集进行训练

lr = LinearRegression() #定义一个线性回归对象
lr.fit(x_train,y_train) # 训练模型

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

输出训练集的拟合的确定系数r方

lr.score(x_train,y_train) #输出训练集的拟合的确定系数r方

0.6104887413345148

对测试集进行预测

y_predict=lr.predict(x_test) # 用模型预测

输出测试集集的拟合的确定系数r方

print(lr.score(x_test,y_test))   #输出测试集的拟合的确定系数r方
print(r2_score(y_test,y_predict)) #输出测试集的拟合的确定系数r方

0.6266549097602836
0.6266549097602836

输出测试集的预测的均方误差MSE

diff1=y_predict-y_test
diff2=np.square(diff1)
MSE=np.mean(diff2)
# MSE=sum(diff2)/len(diff1)
print(MSE)

99270.18170164275

plt.rc('font', family='SimHei', size=15) #绘图中的中文显示问题，图表字体为SimHei，字号为15
#plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

# 预测值和真实值画图比较
plt.figure(figsize=(9,8))  
plt.scatter(y_test,y_predict,c='',marker = 'o',edgecolors='k')  #空心圆
plt.xlabel("真实值")
plt.ylabel("预测值")
plt.title("线性回归预测值和真实值之间的关系", fontsize=20)
plt.grid(b=True)#加网格
plt.savefig('线性回归预测值和真实值之间的关系') #保存图片文件命名为

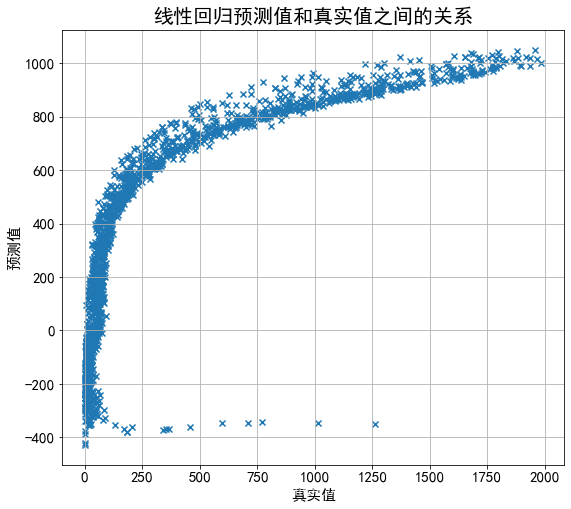
岭回归

# ========岭回归========
model = Ridge(alpha=0.5)
# model = RidgeCV(alphas=[0.1, 1.0, 10.0])  # 通过RidgeCV可以设置多个参数值，算法使用交叉验证获取最佳参数值
model.fit(x_train,y_train)   # 线性回归建模
# print('系数矩阵:\n',model.coef_)
# print('线性回归模型:\n',model)
# print('交叉验证最佳alpha值',model.alpha_)  # 只有在使用RidgeCV算法时才有效
# 使用模型预测
predict = model.predict(x_test)

print('输出训练集的拟合的确定系数r方',model.score(x_train,y_train)) #输出训练集的拟合的确定系数r方
print('输出测试集的拟合的确定系数r方',model.score(x_test,y_test)) #输出测试集的拟合的确定系数r方
print(r2_score(y_test,predict)) #输出测试集的拟合的确定系数r方

diff1=predict-y_test
diff2=np.square(diff1)
MSE=np.mean(diff2)
# MSE=sum(diff2)/len(diff1)
print('测试集的预测的均方误差MSE',MSE)

plt.figure(figsize=(9,8))  
# 绘制散点图 参数：x横轴 y纵轴
plt.scatter(y_test, predict, marker='x')
# 绘制x轴和y轴坐标
plt.xlabel("真实值")
plt.ylabel("预测值")
plt.title("线性回归预测值和真实值之间的关系", fontsize=20)
plt.grid(b=True)#加网格

输出训练集的拟合的确定系数r方 0.610488740485825
输出测试集的拟合的确定系数r方 0.6266547516006221
0.6266547516006221
测试集的预测的均方误差MSE 99270.22375533178