【JAVA】第十一届蓝桥杯省模拟赛答案(本科组)
目录
本辣鸡持续垃圾,一到六题特别简单,做到第七题有点绕,做到第八、九、十题就不想做了,晚上补缺失的代码和题解。
一、无向连通图包含多少条边
问题描述
一个包含有2019个结点的无向连通图,最少包含多少条边?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
题解
一个有n个顶点的无向连通图最多有n(n-1)/2条边,最少有n-1条边。
答案
2018
二、字母重新排列
问题描述
将LANQIAO中的字母重新排列,可以得到不同的单词,如LANQIAO、AAILNOQ等,注意这7个字母都要被用上,单词不一定有具体的英文意义。
请问,总共能排列如多少个不同的单词。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
题解
本题看似是全排列,实际不是,因为有两个A,
解题算式:
A77/A22 (这里都是排列的计算公式,参见Anm,n为下标,m为上标)
也就是(7x6x5x4x3x2x1)/2x1=2520
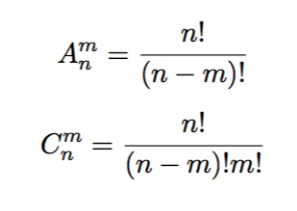

答案
2520
三、在计算机存储中,12.5MB是多少字节?
问题描述
在计算机存储中,12.5MB是多少字节?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
题解
这是真的送分题
12.5*1024(转换成KB)*1024(转换成B)=13,107,200

答案
13107200
四、合法括号序列
问题描述
由1对括号,可以组成一种合法括号序列:()。
由2对括号,可以组成两种合法括号序列:()()、(())。
由4对括号组成的合法括号序列一共有多少种?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
题解
手算,极其不推荐,太容易漏了
这是一个填空题,只需要填写答案即可。
这里深度为1的序列有一种为:()()()(),
深度为2的有7种:(())()()、()(())()、()()(())、(()()())、(()())()、()(()())、(())(()),
深度为3的有5种:((()))()、()((()))、((())())、(()(()))、((()())),
深度为4的有1种:(((()))),
所以答案为14。
代码
public class LegalBrackets {
public static int count = 0, n = 4;
public static void main(String[] args) {
f(0, 0);
System.out.println(count);
}
public static void f(int left, int right) {
if (left == n) {
count++;
return;
}
f(left + 1, right);
if (left > right) {
f(left, right + 1);
}
}
}
答案
14
五、凯撒密码
问题描述
给定一个单词,请使用凯撒密码将这个单词加密。
凯撒密码是一种替换加密的技术,单词中的所有字母都在字母表上向后偏移3位后被替换成密文。即a变为d,b变为e,…,w变为z,x变为a,y变为b,z变为c。
例如,lanqiao会变成odqtldr。
输入格式
输入一行,包含一个单词,单词中只包含小写英文字母。
输出格式
输出一行,表示加密后的密文。
样例输入
lanqiao
样例输出
odqtldr
评测用例规模与约定
对于所有评测用例,单词中的字母个数不超过100
代码
import java.util.Scanner;
public class 凯撒密码 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.next();
sc.close();
char[] chars = s.toCharArray();
StringBuilder result = new StringBuilder();
for (char i : chars) {
if (i == 'x') {
result.append('a');
} else if (i == 'y') {
result.append('b');
} else if (i == 'z') {
result.append('c');
} else {
result.append((char) (i + 3));
}
}
System.out.println(result);
}
}
六、反倍数
问题描述
给定三个整数 a, b, c,如果一个整数既不是 a 的整数倍也不是 b 的整数倍还不是 c 的整数倍,则这个数称为反倍数。
请问在 1 至 n 中有多少个反倍数。
输入格式
输入的第一行包含一个整数 n。
第二行包含三个整数 a, b, c,相邻两个数之间用一个空格分隔。
输出格式
输出一行包含一个整数,表示答案。
样例输入
30
2 3 6
样例输出
10
样例说明
以下这些数满足要求:1, 5, 7, 11, 13, 17, 19, 23, 25, 29。
评测用例规模与约定
对于 40% 的评测用例,1 <= n <= 10000。
对于 80% 的评测用例,1 <= n <= 100000。
对于所有评测用例,1 <= n <= 1000000,1 <= a <= n,1 <= b <= n,1 <= c <= n。
解题思路:暴力就完事了
代码
import java.util.Scanner;
public class 反倍数 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
sc.close();
int count = 0;
for (int i = 1; i <= n; i++) {
if (i % a != 0 && i % b != 0 && i % c != 0) {
count++;
}
}
System.out.println(count);
}
}
七、螺旋矩阵
问题描述
对于一个 n 行 m 列的表格,我们可以使用螺旋的方式给表格依次填上正整数,我们称填好的表格为一个螺旋矩阵。
例如,一个 4 行 5 列的螺旋矩阵如下:
1 2 3 4 5
14 15 16 17 6
13 20 19 18 7
12 11 10 9 8
输入格式
输入的第一行包含两个整数 n, m,分别表示螺旋矩阵的行数和列数。
第二行包含两个整数 r, c,表示要求的行号和列号。
输出格式
输出一个整数,表示螺旋矩阵中第 r 行第 c 列的元素的值。
样例输入
4 5
2 2
样例输出
15
评测用例规模与约定
对于 30% 的评测用例,2 <= n, m <= 20。
对于 70% 的评测用例,2 <= n, m <= 100。
对于所有评测用例,2 <= n, m <= 1000,1 <= r <= n,1 <= c <= m。
代码
import java.util.Scanner;
public class 螺旋矩阵 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int r = sc.nextInt();
int c = sc.nextInt();
sc.close();
int[][] matrix = new int[n][m];
int temp = 1;
int upBound = 0;
int rightBound = m - 1; //4
int leftBound = 0;
int downBound = n - 1; //3
while (true) {
//1000*1000复杂度应该不会超时
//四个方向放数,上下左右四个循环
//上面放最上面一行的,下面最下面一行的,如果放完数的话就可以pass这一层了
for (int i = leftBound; i <= rightBound; ++i)
matrix[upBound][i] = temp++;
if (++upBound > downBound) break;
for (int i = upBound; i <= downBound; ++i)
matrix[i][rightBound] = temp++;
if (--rightBound < leftBound) break;
for (int i = rightBound; i >= leftBound; --i)
matrix[downBound][i] = temp++;
if (--downBound < upBound) break;
for (int i = downBound; i >= upBound; --i)
matrix[i][leftBound] = temp++;
if (++leftBound > rightBound) break;
}
//输出矩阵
/*for (int i=0;i<n;i++){
for (int j=0;j<m;j++){
System.out.print(matrix[i][j]+" ");
}
System.out.println();
}*/
System.out.println(matrix[r - 1][c - 1]);
}
}
八、摆动序列
问题描述
如果一个序列的奇数项都比前一项大,偶数项都比前一项小,则称为一个摆动序列。即 a[2i]<a[2i-1], a[2i+1]>a[2i]。
小明想知道,长度为 m,每个数都是 1 到 n 之间的正整数的摆动序列一共有多少个。
输入格式
输入一行包含两个整数 m,n。
输出格式
输出一个整数,表示答案。答案可能很大,请输出答案除以10000的余数。
样例输入
3 4
样例输出
14
样例说明
以下是符合要求的摆动序列:
2 1 2
2 1 3
2 1 4
3 1 2
3 1 3
3 1 4
3 2 3
3 2 4
4 1 2
4 1 3
4 1 4
4 2 3
4 2 4
4 3 4
评测用例规模与约定
对于 20% 的评测用例,1 <= n, m <= 5;
对于 50% 的评测用例,1 <= n, m <= 10;
对于 80% 的评测用例,1 <= n, m <= 100;
对于所有评测用例,1 <= n, m <= 1000。
题解:
使用dp,动态规划
正确代码:
import java.util.Scanner;
public class 正整数的摆动序列 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
int n = sc.nextInt();
sc.close();
//dp[i][j] i表示第多少位,j表示一个分界线
// 奇数行就是大于j的方案数,偶数行就是小于j的方案数
// 奇数要比前面的大,所以要大于的,偶数要比前面的小,所以要小于的
int[][] dp = new int[m+2][n+2];
//初始化边界
for (int i = 1; i <=n; i++) {
dp[1][i]=n-i+1;
}
for(int i = 2; i <= m; i++)
if((i&1)==1){
//奇数的话是要比前面大的,所以用倒序
for(int j = n; j >= 1; j--){
dp[i][j] = (dp[i-1][j-1] + dp[i][j+1]) % 10000;
}
}
else{
for(int j = 1; j <= n; j++){
dp[i][j] = (dp[i-1][j+1] + dp[i][j-1]) % 10000;
}
}
//判断奇偶从此我要改成这个了,一位位运算确实快
//m&1,就是把m换成二进制看看最后一位是不是1,如果是1证明就是奇数,如果是0证明是偶数
int result = (m & 1)==1 ? dp[m][1] : dp[m][n];
System.out.println(result);
}
}
错误代码:
这肯定是错的,但确实是我最初的想法,然后我想整个递归啥的来处理大于3的情况,也没整出来,晚上补个正确代码吧
我最后也把这个代码交了,因为蓝桥杯会有很多组测试用例,你对了其中一两个也是有分的
import java.util.ArrayList;
import java.util.Scanner;
public class Test1 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt(); //长度为 m
int n = sc.nextInt(); //每个数都是 1 到 n 之间的正整数
sc.close();
ArrayList<int[]> array = new ArrayList<int[]>();
int count = 0;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (j < i) {
for (int h = 1; h <= n; h++) {
if (h > j) {
int[] a = new int[3];
a[0] = i;
a[1] = j;
a[2] = h;
array.add(a);
count++;
}
}
}
}
}
/*//输出矩阵
for (int[] i:array){
for (int j=0;j<3;j++){
System.out.print(i[j]+" ");
}
System.out.println();
}*/
System.out.print(count);
}
}
九、小明植树
问题描述
小明和朋友们一起去郊外植树,他们带了一些在自己实验室精心研究出的小树苗。
小明和朋友们一共有 n 个人,他们经过精心挑选,在一块空地上每个人挑选了一个适合植树的位置,总共 n 个。他们准备把自己带的树苗都植下去。
然而,他们遇到了一个困难:有的树苗比较大,而有的位置挨太近,导致两棵树植下去后会撞在一起。
他们将树看成一个圆,圆心在他们找的位置上。如果两棵树对应的圆相交,这两棵树就不适合同时植下(相切不受影响),称为两棵树冲突。
小明和朋友们决定先合计合计,只将其中的一部分树植下去,保证没有互相冲突的树。他们同时希望这些树所能覆盖的面积和(圆面积和)最大。
输入格式
输入的第一行包含一个整数 n ,表示人数,即准备植树的位置数。
接下来 n 行,每行三个整数 x, y, r,表示一棵树在空地上的横、纵坐标和半径。
输出格式
输出一行包含一个整数,表示在不冲突下可以植树的面积和。由于每棵树的面积都是圆周率的整数倍,请输出答案除以圆周率后的值(应当是一个整数)。
样例输入
6
1 1 2
1 4 2
1 7 2
4 1 2
4 4 2
4 7 2
样例输出
12
评测用例规模与约定
对于 30% 的评测用例,1 <= n <= 10;
对于 60% 的评测用例,1 <= n <= 20;
对于所有评测用例,1 <= n <= 30,0 <= x, y <= 1000,1 <= r <= 1000。
题解
使用dfs,深度优先搜索
答案
import java.util.Scanner;
public class 植树2 {
public static boolean[][] bool = new boolean[31][31];
static boolean[] vis = new boolean[31];
public static int[] x = new int[31];
public static int[] y = new int[31];
public static int[] r = new int[31];
public static int n = 0, max = -1;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
for (int i = 1; i <= n; i++) {
x[i] = sc.nextInt();
y[i] = sc.nextInt();
r[i] = sc.nextInt();
}
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
boolean bo = ((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]) > (r[i] + r[j])
* (r[i] + r[j]));
bool[i][j] = bo;
bool[j][i] = bo;
}
}
sc.close();
dfs(1);
System.out.println(max);
}
public static void dfs(int step) {
if (step > n) {
int sum = 0;
for (int i = 1; i <= n; i++) {
if (vis[i]) {
sum += (r[i] * r[i]);
}
}
max = Math.max(sum, max);
return;
}
vis[step] = false;
dfs(step + 1);
for (int i = 1; i < step; i++) {
if (vis[i] && !bool[i][step]) {
return;
}
}
vis[step] = true;
dfs(step + 1);
}
}
十、全国户户通电
问题描述
2015年,全中国实现了户户通电。作为一名电力建设者,小明正在帮助一带一路上的国家通电。
这一次,小明要帮助 n 个村庄通电,其中 1 号村庄正好可以建立一个发电站,所发的电足够所有村庄使用。
现在,这 n 个村庄之间都没有电线相连,小明主要要做的是架设电线连接这些村庄,使得所有村庄都直接或间接的与发电站相通。
小明测量了所有村庄的位置(坐标)和高度,如果要连接两个村庄,小明需要花费两个村庄之间的坐标距离加上高度差的平方,形式化描述为坐标为 (x_1, y_1) 高度为 h_1 的村庄与坐标为 (x_2, y_2) 高度为 h_2 的村庄之间连接的费用为
sqrt((x_1-x_2)(x_1-x_2)+(y_1-y_2)(y_1-y_2))+(h_1-h_2)*(h_1-h_2)。
在上式中 sqrt 表示取括号内的平方根。请注意括号的位置,高度的计算方式与横纵坐标的计算方式不同。
由于经费有限,请帮助小明计算他至少要花费多少费用才能使这 n 个村庄都通电。
输入格式
输入的第一行包含一个整数 n ,表示村庄的数量。
接下来 n 行,每个三个整数 x, y, h,分别表示一个村庄的横、纵坐标和高度,其中第一个村庄可以建立发电站。
输出格式
输出一行,包含一个实数,四舍五入保留 2 位小数,表示答案。
样例输入
4
1 1 3
9 9 7
8 8 6
4 5 4
样例输出
17.41
评测用例规模与约定
对于 30% 的评测用例,1 <= n <= 10;
对于 60% 的评测用例,1 <= n <= 100;
对于所有评测用例,1 <= n <= 1000,0 <= x, y, h <= 10000。
题解
答案
import java.util.Arrays;
import java.util.Scanner;
public class 户户通电 {
static class Node {
int x;
int y;
int h;
}
public static void main(String[] args) {
//输入
Node[] nodes = new Node[1002];
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for (int i = 1; i <= n; i++) {
nodes[i]=new Node();
nodes[i].x = sc.nextInt();
nodes[i].y = sc.nextInt();
nodes[i].h = sc.nextInt();
}
sc.close();
//初始化数组
double[][] map = new double[n + 2][n + 2];
double[] mins = new double[n + 2]; //这个最后是用来保存最小值的
double MAX = 0x7f7f7f7f;
for (int i = 0; i <= n+1; i++) {
for (int j = 0; j <=n+1; j++) {
map[i][j]=MAX;
}
mins[i] = MAX;
}
//先找到每个值的最短路
for (int i = 1; i <= n-1; i++) {
for (int j = i + 1; j <= n; j++) {
double x = (nodes[i].x - nodes[j].x) * (nodes[i].x - nodes[j].x);
double y = (nodes[i].y - nodes[j].y) * (nodes[i].y - nodes[j].y);
double h = (nodes[i].h - nodes[j].h) * (nodes[i].h - nodes[j].h);
double temp=Math.sqrt(x+y)+h;
map[i][j]=Math.min(map[i][j],temp );
map[j][i]=map[i][j];
}
}
//然后图算法公式
boolean[] vis = new boolean[n+2];
mins[1]=0;
for (int i = 1; i <n; i++) {
int tempX=0;
for (int j = 1; j <=n; j++) {
if(!vis[j] &&(tempX==0|| mins[j]<mins[tempX])){
tempX=j;
}
}
vis[tempX]=true;
for (int j = 1; j <=n; j++) {
if(!vis[j]){
mins[j]=Math.min(mins[j], map[tempX][j]);
}
}
}
double result=0.0;
for (int i = 2; i <=n; i++) {
result+=mins[i];
}
System.out.println(result);
}
}


