本篇是该系列的第六篇,承接上篇IZigZag变换,介绍接下来的一个步骤——逆离散余弦变换,即逆零偏置前的一个步骤。
该步骤比较偏理论,其业务是对IZigZag变换后的数据,再进一步的处理,使其恢复DCT变换前的数据。
需要补充一点说明的是,上面的DCT其实是DCT2,因为jpeg编码下都是对8x8的像素块进行处理。
1. 理论
1.1. 背景
DCT,即离散余弦变换,常用图像压缩算法,步骤如下
1)分割,首先将图像分割成8x8或16x16的小块;
2)DCT变换,对每个小块进行DCT变换;
3)舍弃高频系数(AC系数),保留低频信息(DC系数)。高频系数一般保存的是图像的边界、纹理信息,低频信息主要是保存的图像中平坦区域信息。
4)图像的低频和高频,高频区域指的是空域图像中突变程度大的区域(比如目标边界区域),通常的纹理丰富区域。
1.2.算法
二维DCT变换就是将二维图像从空间域转换到频率域。形象的说,就是计算出图像由哪些二维余弦波构成。其算法如下:

其中,F就是变换得到的系数,f是图像的像素值,A是转换矩阵,其中i为二维波的水平方向频率,j为二维波的垂直方向频率,取值范围都是0-(N-1),N是图像块的大小,其中:

即进行如下步骤的处理可以得到DCT变换后的系数矩阵:
1)求出转换矩阵A;
2)利用转换矩阵A,转换到频域,即由图像 f 得到系数矩阵F。
2. 实践
2.1. 图像上运用实现
DCT用图像上的处理,都是对8x8的像素数据块进行处理,因此,DCT2变换的转换矩阵A为:
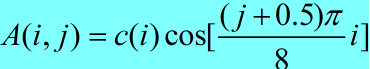
其中,

那么转换矩阵A为:

计算如这个链接:
1 void InitTransMat()
2 {
3 int i,j;
4 float a;
5
6 for(i=0;i<MAT_SIZE;i++)
7 {
8 for(j=0;j<MAT_SIZE;j++)
9 {
10 a = 0;
11 if(i==0)
12 {
13 a=sqrt((float)1/MAT_SIZE);
14 }
15 else
16 {
17 a=sqrt((float)2/MAT_SIZE);
18 }
19 DCT_Mat[i][j]= a*cos((j+0.5)*PI*i/MAT_SIZE); //变换矩阵
20 }
21 }
22 /* only for 8x8 */
23 //float Tmp[100][100] = {
24 // {0.3536, 0.3536, 0.3536, 0.3536, 0.3536, 0.3536, 0.3536, 0.3536,},
25 // {0.4904, 0.4157, 0.2778, 0.0975, -0.0975, -0.2778, -0.4157, -0.4904,},
26 // {0.4619, 0.1913, -0.1913, -0.4619, -0.4619, -0.1913, 0.1913, 0.4619,},
27 // {0.4157, -0.0975, -0.4904, -0.2778, 0.2778, 0.4904, 0.0975, -0.4157,},
28 // {0.3536, -0.3536, -0.3536, 0.3536, 0.3536, -0.3536, -0.3536, 0.3536,},
29 // {0.2778, -0.4904, 0.0975, 0.4157, -0.4157, -0.0975, 0.4904, -0.2778,},
30 // {0.1913, -0.4619, 0.4619, -0.1913, -0.1913, 0.4619, -0.4619, 0.1913,},
31 // {0.0975, -0.2778, 0.4157, -0.4904, 0.4904, -0.4157, 0.2778, -0.0975,},
32 //};
33 //for (int i=0; i<8; i++)
34 // for (int j=0; j<8; j++)
35 // DCT_Mat[i][j] = Tmp[i][j];
36 }
2.2. IDCT2—— 由F求f的过程
前篇文章已介绍了由IZigZag变换后得到的系数矩阵F,那么要恢复原数据,就要进行如下变换:
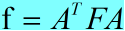
算法的C语言描述如下:
1 int IDCT2(float (*dst)[8], int (*block)[8], bool dump)
2 {
3 float trans_matrix[8][8] = {
4 {0.3536, 0.3536, 0.3536, 0.3536, 0.3536, 0.3536, 0.3536, 0.3536,},
5 {0.4904, 0.4157, 0.2778, 0.0975, -0.0975, -0.2778, -0.4157, -0.4904,},
6 {0.4619, 0.1913, -0.1913, -0.4619, -0.4619, -0.1913, 0.1913, 0.4619,},
7 {0.4157, -0.0975, -0.4904, -0.2778, 0.2778, 0.4904, 0.0975, -0.4157,},
8 {0.3536, -0.3536, -0.3536, 0.3536, 0.3536, -0.3536, -0.3536, 0.3536,},
9 {0.2778, -0.4904, 0.0975, 0.4157, -0.4157, -0.0975, 0.4904, -0.2778,},
10 {0.1913, -0.4619, 0.4619, -0.1913, -0.1913, 0.4619, -0.4619, 0.1913,},
11 {0.0975, -0.2778, 0.4157, -0.4904, 0.4904, -0.4157, 0.2778, -0.0975,},
12 };
13
14 float tmp[8][8];
15
16 float t=0;
17 int i,j,k;
18 for(i=0;i<8;i++) //same as A'*I
19 {
20 for(j=0;j<8;j++)
21 {
22 t = 0;
23 for(k=0; k<8; k++)
24 {
25 t += trans_matrix[k][i] * block[k][j]; //trans_matrix's ith column * block's jth column
26 }
27 tmp[i][j] = t;
28 }
29 }
30
31 for(i=0; i<8; i++) //same as tmp*A
32 {
33 for(j=0; j<8; j++)
34 {
35 t=0;
36 for(k=0; k<8; k++)
37 {
38 t += tmp[i][k] * trans_matrix[k][j];
39 }
40 dst[i][j] = t;
41 }
42 }
43
44 if (dump) {
45 puts("----after idct2----");
46 for (i=0; i<8; i++) {
47 for (j=0; j<8; j++) {
48 printf("%3.4f ", dst[i][j]);
49 }
50 puts("");
51 }
52 puts("");
53 }
54
55 return 0;
56 }
2.3. 例子实践
根据前篇文章的IZigZag结果恢复数据,如下:
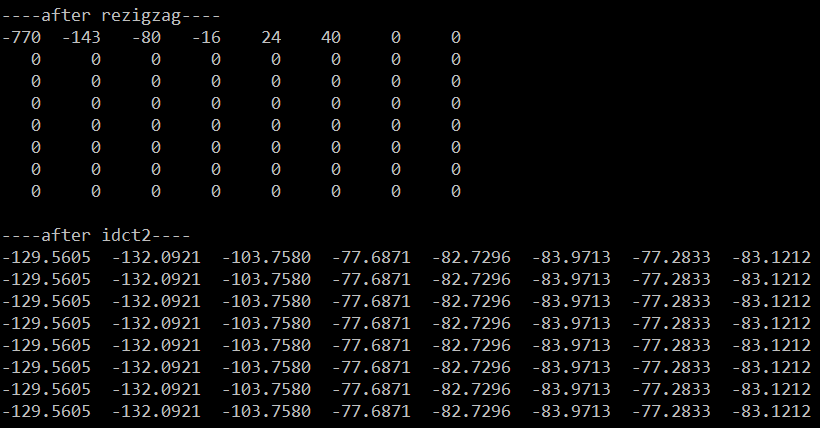
有没有注意到许多值是近似相等的?这是因为图像在时域的连续性导致,可以利用其进行数据压缩。
3. 篇外补充
正是图像上这种特性,才有了图像压缩的这种方法——空间去冗余。
但是,需要说明一点的是,DCT2/IDCT2不是有损失压缩(压缩是数据量降低的概念,有损/无损是转换前后信息是否丢失的概念),因为它可以完全恢复数据,只是这种变换将图像在空间域/频率域之间转换。另外因为本人用的是浮点运算,因此会降低运算速度。一种优化可以把变换矩阵表每个元素都扩大10000倍,进行整形运算。
从DCT正变换角度来说,时域的非0数据量很多,但是经DCT2转换后,频域(非0数据)数据量变得非常少,值都普遍缩小,很多较大的非零值转换为了0,后续可以用其他算子来表示一连串连续的零数据。
在这里,要特别感谢傅里叶这位法国数学家,正是因为他的出色工作,才使得如今的最常见的图像压缩技术变成了现实。
正可谓,前人栽树后人乘凉。前人的理论成果,后人在应用上开花结果。



