本篇是该系列的第四篇，承接前篇的文件头解析，主要介绍霍夫曼解码相关内容。
承接上篇，文件头解析完毕后，就进入了编码数据区域，即SOS的tag后的区域，也是图片数据量的大头所在。
1. 待处理的数据区域
一个例子来说明，仍使用那张animal_park.jpg的图片。
其二进制数据显示如下（FFDA所代表的SOS之后深色标注区域）：
截取到的二进制数据为：F9 96 8B FA 71 EA 5B 24 B5 ...
2. 解码过程规则描述
a）从此颜色分量单元数据流的起点开始一位一位的读入，直到读入的编码与该分量直流哈夫曼树的某个码字（叶子结点）一致，然后用直流哈夫曼树
查得该码字对应的权值。权值（共8位）表示该直流分量数值的二进制位数，也就是接下来需要读入的位数。
b）继续读入位数据，直到读入的编码与该分量交流哈夫曼树的某个码字（叶子结点）一致，然后用交流哈夫曼树查得该码字对应的权值。权值的高4位
表示当前数值前面有多少个连续的零，低4 位表示该交流分量数值的二进制位数，也就是接下来需要读入的位数。
c）不断重复步骤b，直到满足交流分量数据结束的条件。
而结束条件有两个，只要满足其中一个即可：
①当读入码字的权值为零，表示往后的交流变量全部为零；
②已经读入63个交流分量。
3. 准备工作——霍夫曼表
在解析文件头时，会得到四张霍夫曼表——DC0,AC0, DC1,AC1，待后面解码时使用。
DC0——Y分量的直流部分
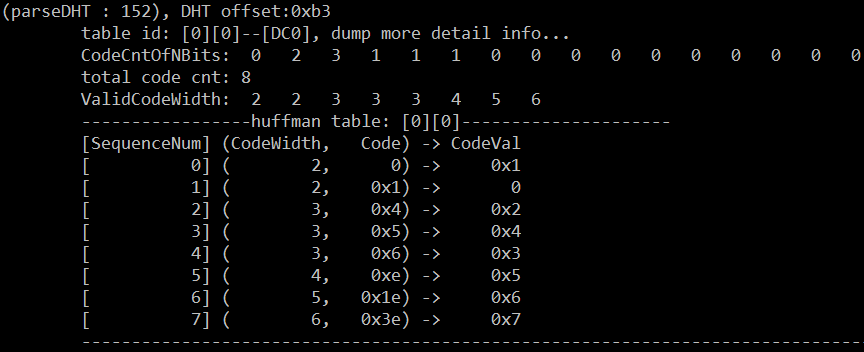
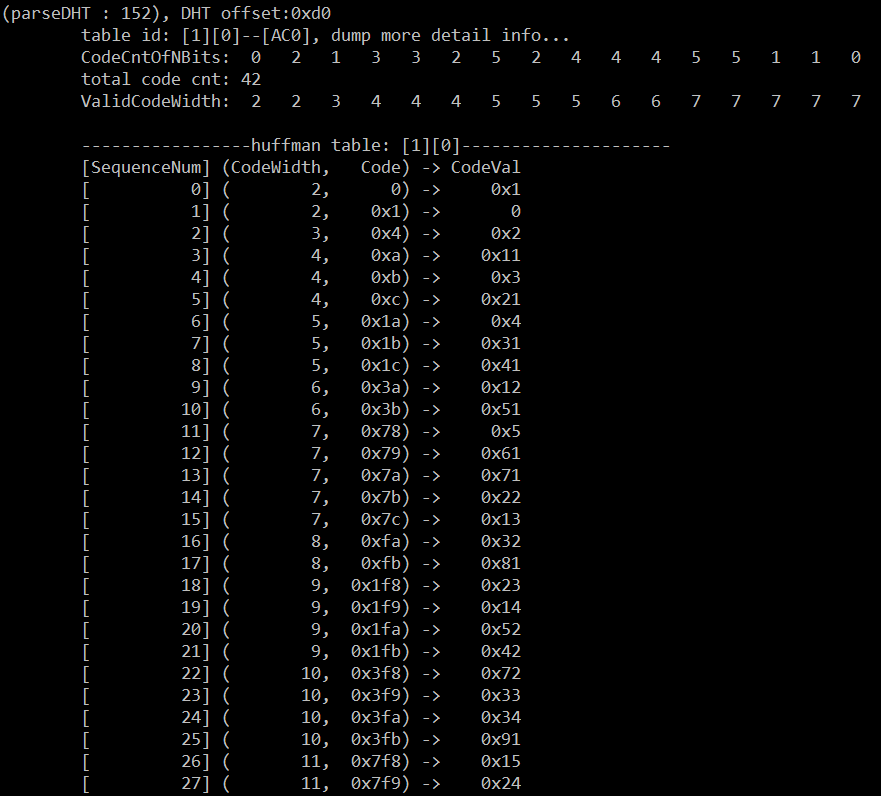
AC0——Y分量的交流部分（表太长，没列全）
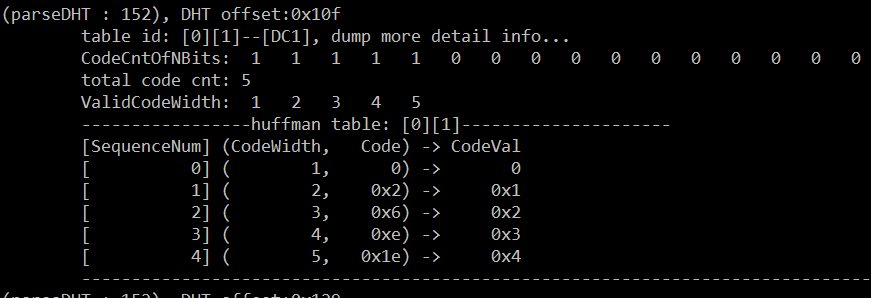
DC1——UV分量的直流部分
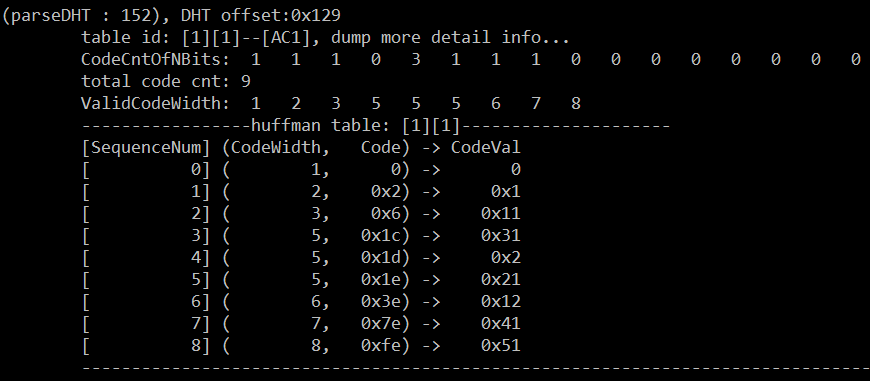
AC1——UV分量的交流部分
4. 解码步骤
这是难点所在，解码的过程其实就是霍夫曼树的查找过程。mcu单元内部使用了RLE行程编码和霍夫曼编码来压缩数据。
此时，正需要一个例子来实战说明，因为理论是对实践的抽象。
例子：F9 96 8B FA 71 EA 5B 24 B5。。。
对应的二进制位展开：1111 1001, 1001 0110, 1000 1011, 1111 1010, 0111 0001, 1110 1010, 0101 1011, 0010 0100, 1011 0101。。。
step1. 先读入若干位与DC0表的Code进行匹配。
读取2位的11时， 无匹配的Code，因为2位宽的Code只有0b00和0b01
3位的111 无 3 0b100，0b101和0b110。
4位的1111 无 4 0b1110。
5位的11111 无 5 0b11110。
6位的111110 有 6 0b111110，恰好匹配！其对应的CodeVal为0x7
step2. 利用上面得到的CodeVal进行拆分，并读取后面若干位。
0x7=0x07，高四位为0，低四位为7，则再读取后面的7位二进制，为：01, 1001 0。
后面读取的值，这样算：如果开头为1则为正数，如果开头为0，则为负数，然后对各位求反得到数值，即可。
01, 1001 0这个值，由于开头为0，则为负数，多少呢？取反得到：10, 01101 = 0x4D = 77，最后得到最终值为：-77。
step3. 通过上面两步骤的第一次扫描，得到的为Y分量的DC值，后面还需经过63次扫描得到剩余的AC值（一般扫描几次就结束了）。
上面DC值标记为-77。
step4. 继续通过类似step1和step2来取得AC值，注意要查找AC0表。
读取5位的110, 10时，有匹配的Code：0b11010=0x1a，其对应的CodeVal=0x04；
取得后四位的值——4，表示还需读取的二进制位数量，来表示真正的信源值——0b0010，经（step2中描述）变换后值为-13；
那么可以RLE标记为（0，-13），其中0来自于CodeVal的高4位，-13为另读入的数据值。可也记为key-val对。
step5. 重复step4的操作，直到得到(0，0)(位置为5B那个字节的最高四位)。
后面的依次为：
Code CodeVal RLE_val RLE
11, 1111 1010(0x3FA) 0x34 0111(-8) (3, -8)
00 0x1 0 (-1) (0, -1)
1, 1110 10(0x7A) 0x71 1(1) (7, 1)
0, 0 0x1 1(1) (0, 1)
01 0x0 -- (0, 0) -> 结束于5B的高4位
为更直观的介绍解析结果，将二进制位数据进行划分，表示如下：
未标记的hex表示： F9 96 8B FA 71 EA 5B 24 B5。。。
未标记的binary表示：1111 1001, 1001 0110, 1000 1011, 1111 1010, 0111 0001, 1110 1010, 0101 1011, 0010 0100, 1011 0101。。。
标记后的binary表示：1111 1001, 1001 0110, 1000 1011, 1111 1010, 0111 0001, 1110 1010, 0101 1011, 0010 0100, 1011 0101。。。
红色表示为查表得到的Code，蓝色表示RLE_val（其二进制位长度为CodecVal后四位值）。
step6. 通过step1-step5的扫描，得到RLE表：-77, (0, -13), (3, -8),(0, -1),(7, 1), (0, 1), (0, 0)
step7. step1到step6结束后，表示一个mcu的霍夫曼解码结束，则可以进行8x8的矩阵展开。
RLE中的(m,n)，m表示前面填充0的个数，n表示实际值。
根据RLE表，其霍夫曼解码结果如下：
5. 一些思考总结
由此huffman decode后得到的表，可以看出其巨大优势，仅仅使用了6Bytes+4bits就表示了8*8=64Bytes的数据量，体现了用时间换空间的
特点，即增加更多计算工作，来减少数据存储空间。
同时，还需要注意以下几点：
a). 接下来根据Y分量采样因子来确定后续是Y分量的表还是UV分量的表。
如果Y/U/V采样因子都为1x1，则接下来依次得到U和V分量的表，再后面继续为Y分量的表；
如果Y分量采样因子为2x2，即最常见的YUV420格式（每2x2个像素点，进行2x2个Y分量采样，以及1x1个U和V分量采样），则当前的已得到
的表为Y00，后续的表为Y01，Y10和Y11，然后才能是U分量的表和V分量的表。
因为采样是按照block为原子单位展开，如下图所示（黑色点表示一个block）：
这里需要补充几个名词：
block——8x8的像素采样表。
MCU——根据采样因子确定的一个完整编码单元。
针对YUV420的2x2的Y分量采样率，其关系如下图：
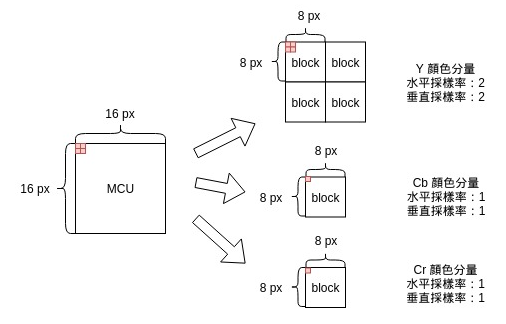
而如果是1x1的采样率，则一个MCU内只包含一个Y分量的block，一个U分量的block和一个V分量的block，图示就不画了。
例如，该图片因为2x2的采样率，则一个MCU的大小位16x16，其包括四个Y分量的block，一个U分量的block和一个V分量的block。
b). 由于DPCM（diff pcm）编码原因，第N个Y分量的DC值保存的是与前面一个的差值。取得第N个值时，扫描出的值再加上前一个值（跨MCU时仍成立）。
接下来的1011, 0010 0100, 1011 0101用于确定Y01的表，根据同样的规则，查表分割如下：
1011, 0010 0100, 1011 0101
得到RLE序列为：9, (0, 1), (0, 1), (0, 0)
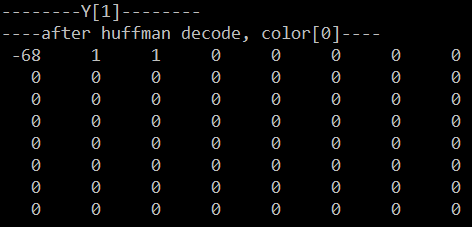
经DPCM修正为：9+(-77)=-68, (0, 1), (0, 1), (0, 0)
如下为重建该block后的表：
c). 由于编码时某些场景会插入某些字节，因此扫描时要跳过某些字节。
