AGC008E Next or Nextnext 解题报告

\(\text{分析}\)

\(i\to a_i\) 构成内向基环树，配合暴力程序观察内向基环树常见的一些特殊情况：

灰色笔对应的是 \(i\to a_i\)，黑色笔对应的是 \(i\to p_i\)，我们相当于要构造一个黑色的排列（若干环）使得每一条灰色边的起点可以通过一条或两条黑色边到达终点。

\(a_i=i\)（全是自环）：

可以任意选择若干对自环配对并连边，显然满足 \(i\to j\to i\)，也可以选择直接 \(i\to i\)。

显然不可能出现三元环或更大的环因为不可能满足 \(i\to j\to i\)。

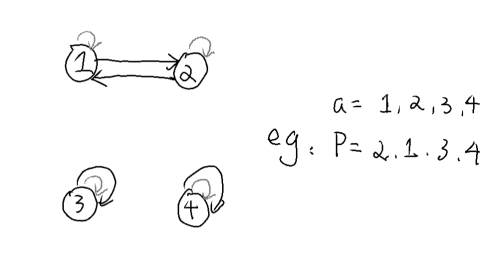
\(a_i=i\bmod n+1\)（一个大的纯环）：

首先显然 \(i\to a_i\) 是一种满足条件的环。

考虑是否存在其它连边方式：存在一个 \(i\) 满足 \(p_{p_i}=a_i\) 的情况，因为环这种情况每个 \(a_i\) 只出现了一次，所以一定有所有 \(i\) 都满足 \(p_{p_i}=a_i\)（两步到达）。

当 \(n\) 是大于 \(1\) 的奇数时，存在一种这样的连边：\(i\to (i+\lceil\frac n 2\rceil) \bmod n\)，满足这种条件，如下图：

容易证明不存在其它连边方式。

两个大小相同的纯环：

假设环之间存在一条连边 \(i\to j\)，那么一定有 \(j\to p_i\)，因此有 \(p_i\to p_j\) ……，可以根据第一条边确定整个环对应的连边方式。

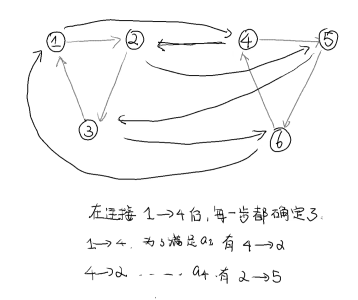
环加一条链：

我们先来考虑这个链只有一个点 \(1\) 的情况：

对于这个链连着的点 \(u\) 存在两个 \(a_x=a_y = u\)，也就说一定是 \(p_x=y,p_y=u\) 或 \(p_y=x,p_x=u\)（因为要求是排列）分别可以对应着下面这两种连接的方法。

对于更长的链也是类似的：在 \(u\) 处选择上一步连接环上或链上 分别对应着提前 \(\text{长度}\) 个点开始交叉链和环，也可以选择提前 \(\text{长度}+1\) 个点开始交叉链和环。

基环树：

当基环树的形态不是“环+若干条链”的时候，即出现了并列的“分叉”情况，那么这个时候分叉的两个点 \(u,v\) 之间必须得是串起来的关系，就无法让 \(x\to u\to v\) 的 \(x\) 满足 \(a_x\) 为 \(p_x\) 或 \(p_{p_x}\) 了。（因为题目的限制导致我们最多同时交叉着走两条链，要是交叉走三条就一定会出现 \(p_{p_x}\) 和 \(p_x\) 都不等于 \(a_x\) 的情况）

所以我们只考虑环+若干条链的这种形态的基环树，显然链之间是独立的，不可能互相连边，于是我们分别考虑每条链可能的情况即可，（从链进入/从环进入）可能的情况取决于这条链在环上离前面的链的长度。

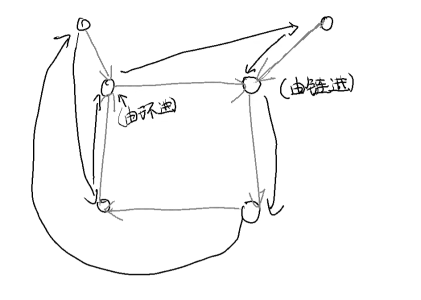
非环的基环树是否可能还会有类似环的另一种连边方式？环的第二种连边方式需要满足所有 \(a_i\) 都为 \(p_{p_i}\)（每一步都确定了），而这个时候就无法让多出来链上的点满足 \(p_i=a_i\) 了。（环的形态固定了，无法接入）

若要连接两个非环的基环树，因为环上部分的连接已经确定，且每步都满足 \(p_{p_i}=a_i\)，因此无法使得有点连向非环的部分，所以非环的基环树一定只能内部连边。

\(\text{结论}\)

我们有着这样一些的连边方式：

• 对于一个任意的环，我们可以让 \(p_i=a_i\)。

• 对于一个任意长度为 \(n=2k+1(k\in \mathbb{N^+})\) 的环，我们可以让 \(p_i=(a^{k+1} )_i\)。（上方有图）

• 对于两个长度都为 \(L\) 的环，我们有 \(L\) 种方式确定第一个环中某一个点连向的第二个环中的点，接下来每一步连接方式都确定了（为了连向上一步的 \(a_i\)），故有 \(L\) 中连接两个环的方法。

• 对于一个非环的基环树，且形态为环加若干条链，我们可以决定每条长度为 \(L\) 的链接入环的位置连向的是环还是链，分别需要对应连接环上前方 \(L\)，\(L+1\) 个点。

\(\text{计数}\)

因为基环树是独立的，我们先把所有基环树找出来并判断形态，然后求出每个点连出去的链长度，然后在环上转圈，找到每个链前面对应的空余长度，根据空余长度和链长度的大小关系分别对应着有 \(0,1,2\) 种连边方式的系数，对所有链的系数求乘积即可。

接下来就考虑若干环之间的连边，每种长度的环是独立的，对于所有环长为 \(L\) 的环，枚举其连接两个环的数量 \(C(2C\leq L)\)，则将这些环配对的方案数为

\[\binom {L}{C,C,L-2C} C! 2^{-C} \]

这个组合数意义很好理解：选出 \(C\) 个与 \(C\) 个之间的对应关系，然后除以 \(2^{C}\) 因为配对关系是无序的，左右等价。

每组环根据不同的错位有 \(L\) 种连法，于是带有 \(L^{C}\) 的系数。

特殊地，若环长 \(L\) 为大于 \(1\) 的奇数，单个的环会有两种连法，再乘上 \(2^{L-2C}\) 即可。

对所有环长的答案求乘法原理，再乘上基环树的方案就是答案。

---

我咋天天场切 3500 啊？感觉这个结论还是蛮好猜的（？）