【题解】P7418 图论 dp 容斥

无脑做法，解构主义。

首先路径不要求是简单的所以可以通过反复走一条边使得路径长度 $+2$。存在长度为 $x$ 的路径意味着一定存在长度为 $x+2$ 的路径，所以我们只关心一个点的奇最短路和偶最短路。

如果原图是一个二分图，那么每个点要么只存在奇路径要么只存在偶路径，所以只关心最短路。按照 $dis_i$ 分层后，每个点连接到上一层即可，答案为 $n-1$。

接下来只考虑原图不是二分图的情况：令到该点的最短路长度为 $x_i$，与最短路径奇偶不同的最短路长度为 $y_i$，我们需要使得新图所有 $(x_i,y_i)$ 和原图相同。

首先有一条边连接的 $(x_u,y_u),(x_v,y_v)$ 一定有 $|x_u-x_v|\leq 1 ,|y_u-y_v| \leq 1$，否则可以用较小者去更新较大者。

所以一个点  $(x,y)$ 只可能和 $(x\pm 1,y\pm 1)$ 连边（当然 $x=y-1$ 时 $(x+1,y-1)$ 为 $(x,y)$ 自己）。

考察一组 $(x,y)$ 的由来，由最短路的构成，一定满足以下两种情况之一：

• 从 $(x-1,y-1)$ 转移来。

• 从 $(x-1,y+1)$ 得到 $x$，从 $(x+1,y-1)$ 得到 $y$（当 $x=y-1$ 时 $(x+1,y-1)$ 为 $(x,y)$ 自己）。

  $(x+1,y+1)$ 可连可不连（对于这个点来说）。

特殊情况是 $x=0$ 即 $1$ 号点不需要向 $(x-1,y+1)$ 连边。

然后接下来的思路很妙：考虑前面二分图按照 $dis$ 分层，而现在难以按照 $dis$ 分层了，分层的目的是为了将原图分成若干个相对较为独立的部分，现在考虑按照 $x+y$ 分层，于是现在只需要考虑每层向上一层连当边和向这一层的左右连的边。

称 $(x-1,y-1)$ 为 $(x,y)$ 的“上面”，$(x-1,y+1)$ 为“左边”，$(x+1,y-1)$ 为“右边”，每个点要么连上面，要么同时连左右（右可能是自环）。

接下来考虑一层一层做。

考虑每层的样子一定形如有若干段，如果不是末尾可以连接自环的段的话一定两个端点都可以向上连。如果末尾可以连接自环那么末尾可能不能向上。（因为这些 $(x,y)$ 是由原图求出来的，所以一定存在一种合法的构造，不会存在一个点上面左右都不能连接），如下：

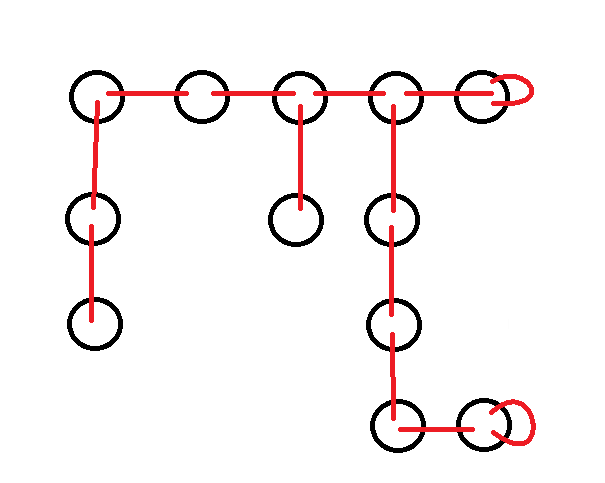
考虑处理每层的每段。

这个限制每个点连接到父亲或左和右侧，就不太好按过程处理，考虑按结果处理：

最终每坨点 $a_i$ 中有 $b_i$ 个没有连接到了上面，我们要求一定连接到了左右，其它 $a_i-b_i$ 个点连接到了上面（连接到的方案数为 $2^{c_i}-1$，其中 $c_i$ 表示上面那坨的点数，这些点不要求连接到左右。

则这段的方案数为（显然要求 $b_1=0$，因为它们无法向左连）：

$$ \sum_{b_i\leq a_i,\forall c_i=0,b_i=a_i} \prod_{i=1} ^n\big((2^{c_i}-1)^{a_i-b_i}\binom {a_i} {b_i}\big)\times\prod_{i=1}^{n-1} f(a_i,b_i,a_{i+1},b_{i+1}) $$

如果这个段末尾的这坨点为 $(x,x+1)$ 即可以内部连边的点，那么我们不要求 $b_n=0$，否则我们要求 $b_n=0$。

其中 $f(n,x,m,y)$ 表示对两坨点连边的方案数，其中第一坨点有 $n$ 个，有 $x$ 个必须连边，第二坨点有 $m$ 个，有 $y$ 个必须连边的方案数。

$f$ 的计算是简单容斥：枚举两边分别有几个不合法。

$$ f(n,m,x,y)=\sum_{i=0}^x\sum_{j=0}^y \binom x i \binom y j 2^{(n-i)(m-j)}\times (-1)^{i+j} $$

可以直接 $O(xy)$ 计算，简单粗暴。

上面那个式子的项相对独立，最多只有相邻两项的相关量。所以可以直接 dp 出来： $dp_{i,j}$ 表示目前处理到了 $1$ 到 $i$，且 $b_i=j$ 的方案数，转移很简单，枚举 $dp_{i-1,v}$ 转移过来并乘上 $f(cnt_{i-1},v,cnt_i,j)$ 即可了。

特殊的是当最右边的点可以内部连边的时候我们需要额外乘上最右边连自环的方案数，假设 $b_n=x$，（即我们有 $x$ 个点必须连边，其它无所谓）需要乘上的额外方案数为 $g(x)$，其中。

这个也是容斥算：枚举钦定几个点不连边。

$$ g(x) = \sum_{i=0}^{cnt}(-1)^{i}\binom {cnt} i \times 2^{\frac{(cnt-i)(cnt-i+1)}{2}} $$

这段的答案就是 $\sum g(x)\times dp_{n,x}$。所有段互不影响，答案求积。

直接做复杂度 $O(n^4)$ 可以通过。

---

优化：

其实 $f$ 的计算可以被优化：

$$ \begin{aligned} &=\sum_{i=0}^x\sum_{j=0}^y \binom x i \binom y j 2^{(n-i)(m-j)}\times (-1)^{i+j}\\ &=\sum_{i=0}^x(-1)^i\binom x i 2^{(n-i)m}\sum_{j=0}^{y}\binom y j (-2^{-(n-i)})^{j} 1^{y-j}\\ &=\sum_{i=0}^x(-1)^i\binom x i 2^{(n-i)m}(-2^{-(n-i)}+1)^{y} \end{aligned} $$

就可以 $O(n^3)$ 了。

---

继续优化：

考虑每次确定状态之后再算 $f$ 很没必要（先定义再容斥），不如直接边 dp 边容斥。考虑容斥非法点的数量，每个非法点只能连左右中的一者不能连父亲，每加入一个非法点带来 $-1$ 的系数。

令 $dp_{i,j}$ 表示第 $i$ 坨点，有 $j$ 个点可以向后连边的容斥系数之和，考虑 $dp_{i-1,c}$ 向 $dp_{i,j}$ 转移 的系数，$cnt-j$ 个点被钦定为不合法，不能向右连边，且必须向左连边（这样它们才不能向右连边）。

然后考虑可以向右连边的 $j$ 个点，就是枚举 $t$ 个钦定不合法的点且没有向左边连边，没有被钦定的点可以向左边任意连边。如下：

$$ \begin{aligned} &\binom{cnt} j\Big((-1)(2^{c}-1)\Big)^{cnt-j}\sum_{t=0}^{j}\binom {j}{t}\times (-1)^{t}\times(2^{c+v})^{j-t} \\ =&\binom{cnt} j(1-2^c)^{cnt-j}(2^{c+v}-1)^{j} \end{aligned} $$

时间复杂度 $O(n^2)$。