P3549 MUL-Multidrink 解题报告

\(\text{0.前言}\)

靠我就打了会儿游戏然后突然想写题解，结果怎么就一点了？？？？

不会又要开始半夜emo了？不至于，但是不想睡觉。有没有人陪我聊会儿天啊/kk。

模拟赛场切留念。

值得一想值得一分析但是不值得一写的题。

这种复杂的题的题解还是要一步一步慢慢来，不能太跳跃也不能瞎扯些深奥的定义。

---

\(\text{1.一些说明}\)

将树以 \(1\) 为根。

“平凡儿子” 指 是叶子的儿子。

“非平凡儿子” 指的是 不是叶子的儿子。

“跳跃” 指从一个儿子跳到它的兄弟。

本文为方便读者理解也方便笔者制作，插入了部分手绘图片，笔者字丑还请见谅（也别在意我用的草稿纸是啥）。

如有笔误或逻辑错误欢迎指出。

---

\(\text{2.初步分析}\)

距离小于等于 \(2\) 就是跳儿子，父亲，兄弟，儿子的儿子和父亲的父亲。

首先题目要求了终点为 \(n\)，又因为一步最多跳的距离是 \(2\)，可以发现走进 \(n\) 的子树后再走出来就无法回到 \(n\) 了，简单证明：

假设一个节点 \(u\)，其儿子中 \(n\) 所在子树为 \(v\)，那么如果想要离开再进入这个子树，一定会经过 \(u\)，\(v\) 之一，即从 \(v\) 跳跃到其它儿子，或者从子树内的一个点跳到 \(u\) 再进入，所以进去出来后就回不去了。

所以对于一个点的所有儿子，我们一定先遍历其它子树并回来，最后一个进入 \(n\) 所在的子树。

---

\(\text{3.寻找思路}\)

和树相关的构造我们一般先考虑链，菊花图之类的特殊的树，我们先来观察一些较为特殊的树：

见下图：

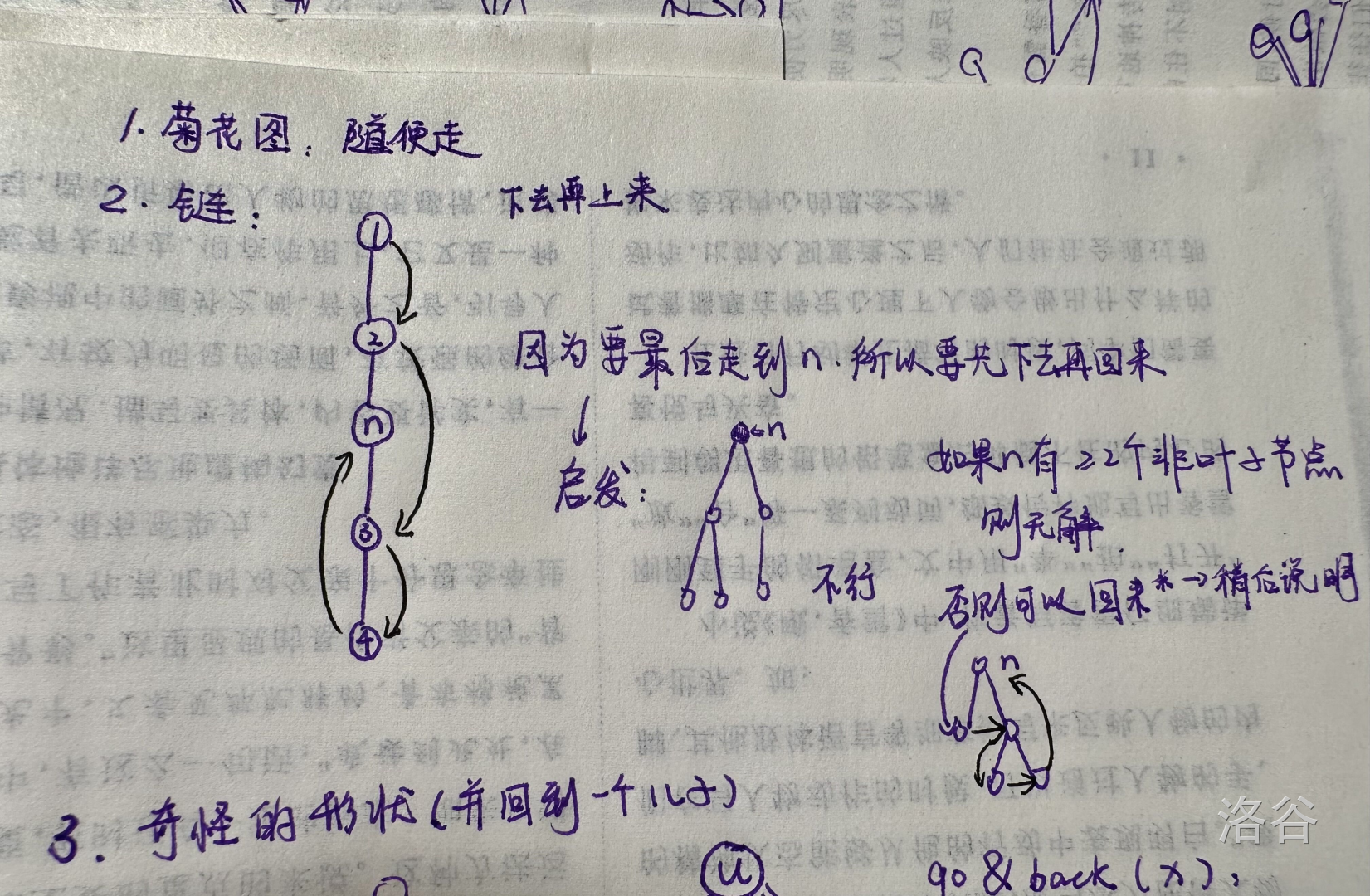
菊花图点两两可以连通，所以随便走即可。

链直接走好像就行？

但是 \(n\) 不一定在链的另一端，所以可能需要跳过 \(n\)，走完下面再回来（如图）。

可以发现如果 \(n\) 有一些儿子，那么我们必须要走到 \(n\) 的父亲，并且其它点已经遍历了，然后下降到 \(n\) 的儿子，遍历完后回到 \(n\)。

---

于是我们现在要处理的一个很关键的行为就是：“遍历某个点的整棵子树，并且回来”，具体地：是回到这个点的一个儿子，因为这样才能跳出这个子树。

于是我们定义操作 \(\text {go(u)}\) 遍历 \(u\) 的子树并回到 \(u\) 的某个儿子的过程。

经过一些分析可以发现，当 \(u\) 的 非平凡儿子 的个数大于一的时候，\(\text {go(u)}\) 不可能实现，简述：

考虑这样一棵树：

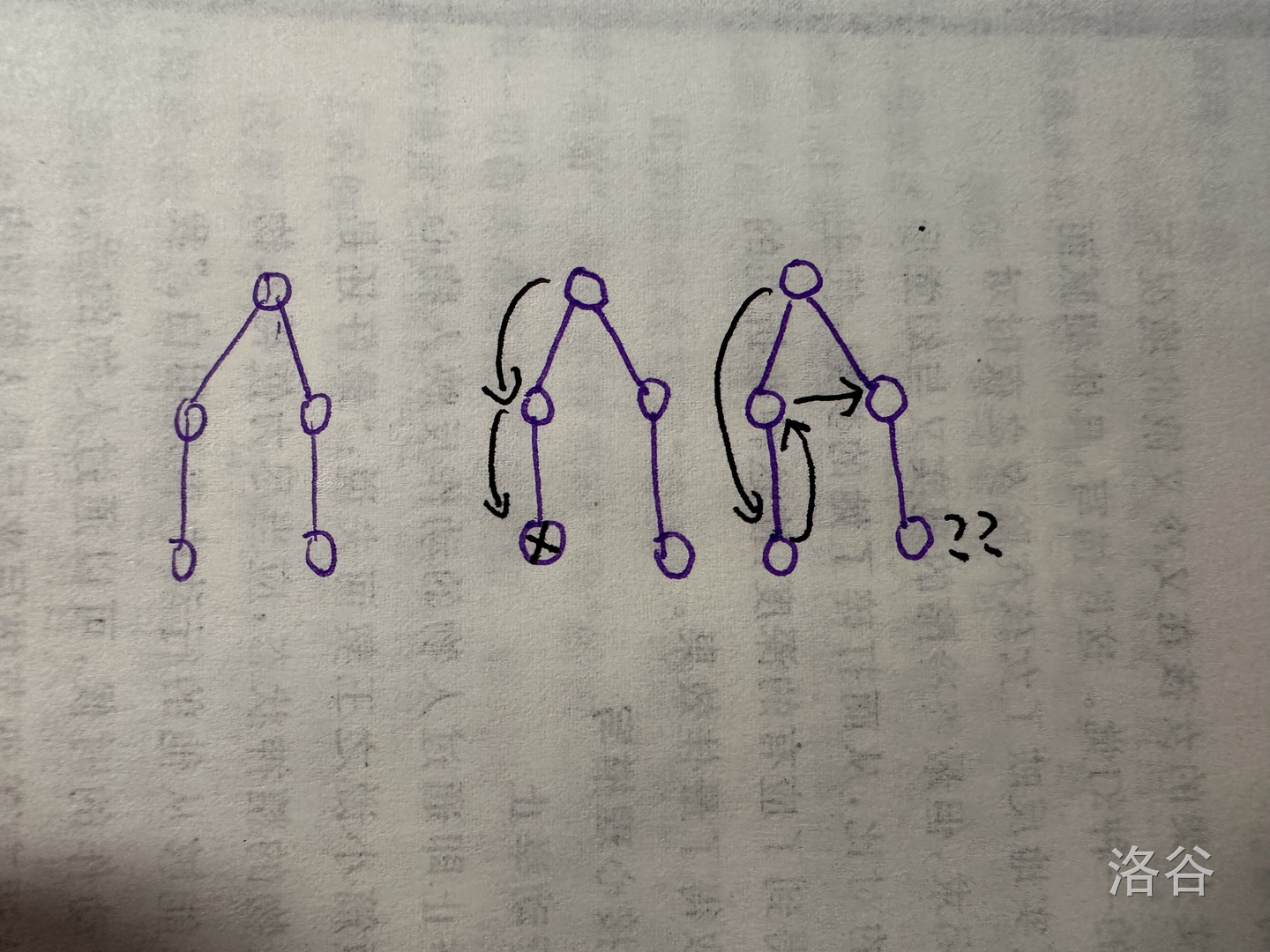
可以发现无论如何都不能实现上述操作，因为进入某个非平凡子树一定会经过它的顶点，而离开也必须要从同一个点离开，所以不行，类似地，这个非平凡儿子也一定只能有不超过一个非平凡儿子。

那么现在 \(u\) 有且仅有一个 非平凡儿子，我们考虑如何构造。（没有非平凡儿子的情况是简单的）

下面给出我观察的另一个结构：（下图左侧）

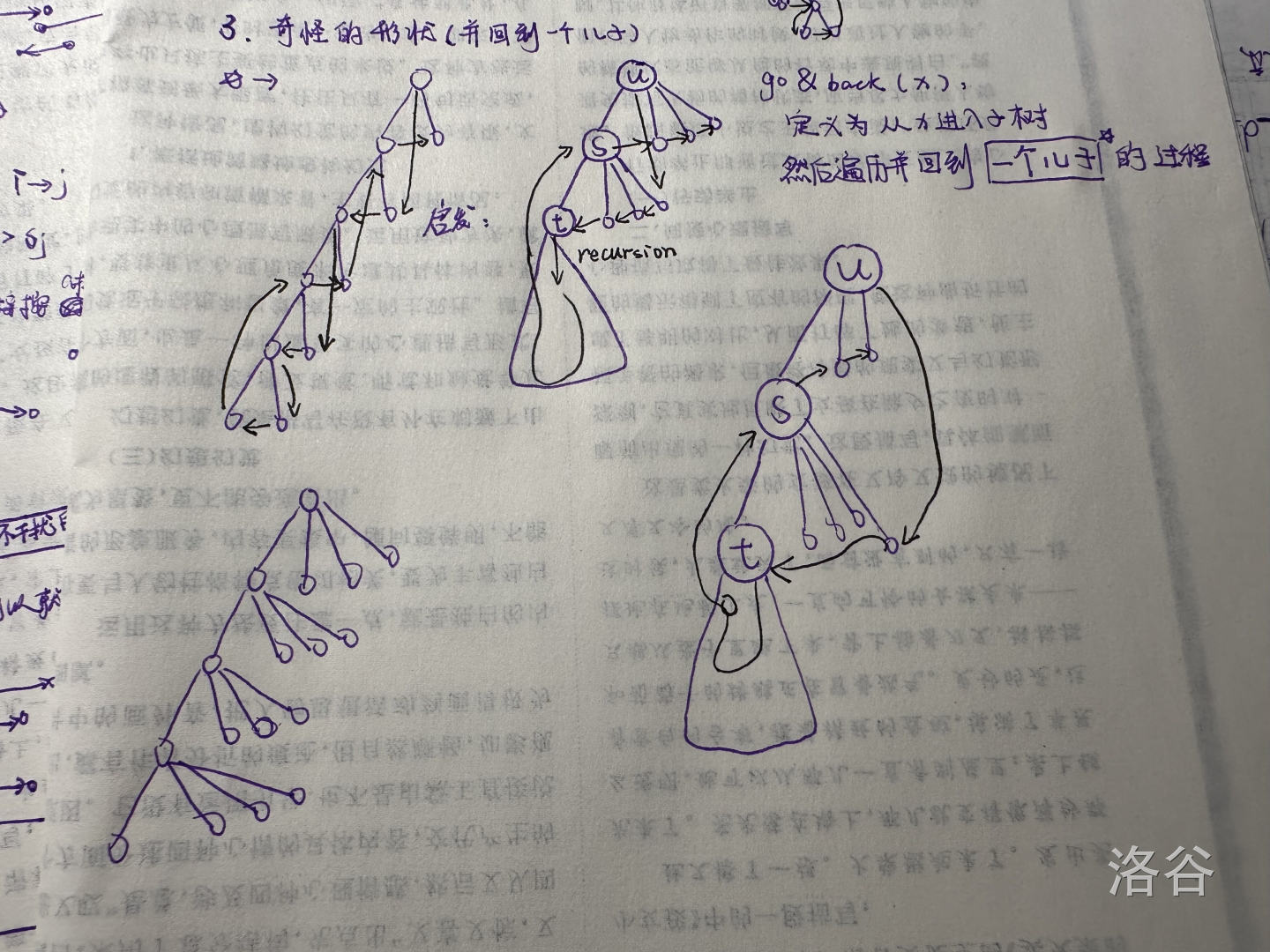
因为有前面的限制，每个点最多有一个非平凡儿子，那么整个树的结构无非就是上图左下的那样，所以我们考虑递归地构造。

（其实大概就是讨论一下非平凡儿子和叶子的访问顺序。）

假设目前在点 \(\text{go(u)}\)，\(u\) 的非平凡儿子是 \(s\)，\(s\) 的非平凡儿子是 \(t\)（如上图），那么有如下遍历方式：

先下降到 \(s\) 的平凡儿子（若没有则直接下降到 \(t\)），在其之间跳跃后跳到 \(t\)，递归执行 \(\text{go(t)}\)，此时在 \(t\) 的一个儿子，则一定可以跳到 \(s\)，然后再在那些平凡的叶子之间跳跃即可，上面图中清晰地画出了路径。

这样构造原因是我们想要让 \(s\) 是在回来时被访问，这样可以访问 \(u\) 的其它平凡儿子，访问 \(t\) 并递归后需要直接回到 \(s\)，所以我们直接遍历 \(s\) 的非平凡儿子再去 \(t\)。

---

\(\text{4.回归原问题}\)

现在重新回到原问题，加入我们目前在一个节点 \(u\) 上，且 \(n\) 在 \(u\) 的子树 \(t\) 中，遍历所有点并走到 \(n\) 的过程，我们称之为 \(\text{solve(u)}\)。

那么类似上面 \(\text{go(x)}\) 中的证明，我们可以发现，\(u\) 除了 \(t\) 之外，最多只能有一棵非平凡子树，否则是无法遍历并去到 \(t\) 的，那么我们令这个非平凡儿子为 \(s\)（没有非平凡儿子的情况是简单的），同理，这个非平凡儿子只能有一个非平凡儿子（否则我们像上面说的那样无法遍历它），然后这个非平凡儿子是 \(p\)，如下图。

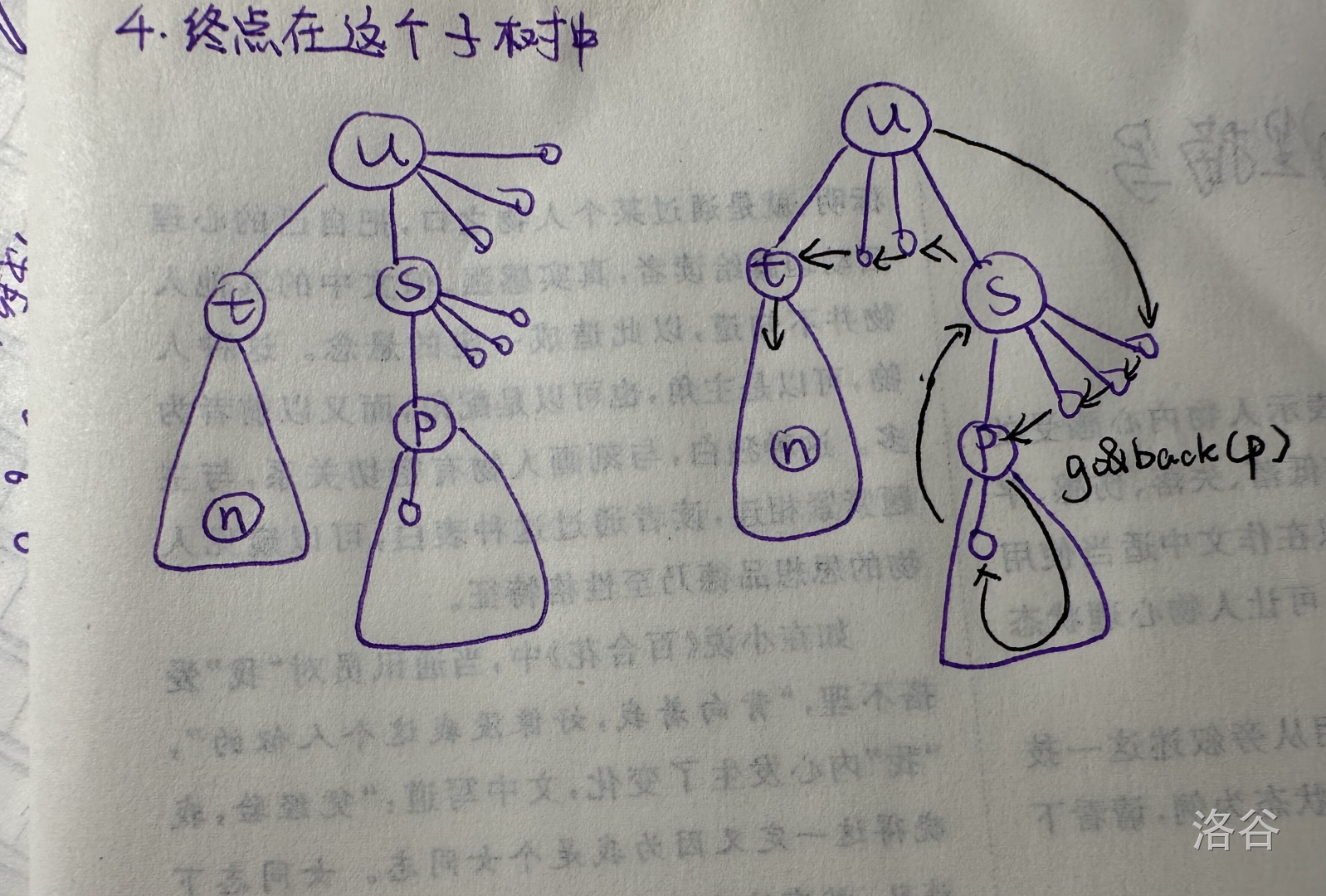
（无非就是讨论下叶子和非平凡儿子的遍历先后顺序）

构造方式（路径在上图中清晰地画出了）：

先下降到 \(s\) 的一个平凡儿子并在其之间跳跃访问完，再访问 \(s\) 的非平凡儿子 \(p\)（若没有则直接访问平凡儿子后返回），并对其执行 \(\text{go(p)}\)，结束后在 \(p\) 的某个儿子（若没有则直接返回），可以跳到 \(s\)，然后再跳到 \(u\) 的其它平凡儿子并在之间跳跃，最后访问 \(t\)，递归执行 \(\text{solve(t)}\)。

---

\(\text{5.特殊情况}\)

（观察样例发现）

当一个点 \(u\) 有且仅有一个儿子 \(t\)，且终点在里面的情况，我们不一定非要访问 \(t\)，之所以前面我们需要访问 \(t\)，是因为其它儿子无法跳到 \(t\) 的子树里，而且\(t\) 必须要被最后访问，所以就只能跳跃到 \(t\) 了。

点 \(u\) 有且仅有儿子 \(t\) 的时候，可以直接跳到 \(t\) 的某个子树后再回到 \(t\)，并执行 \(\text{solve(t)}\) 的操作，举例如图：

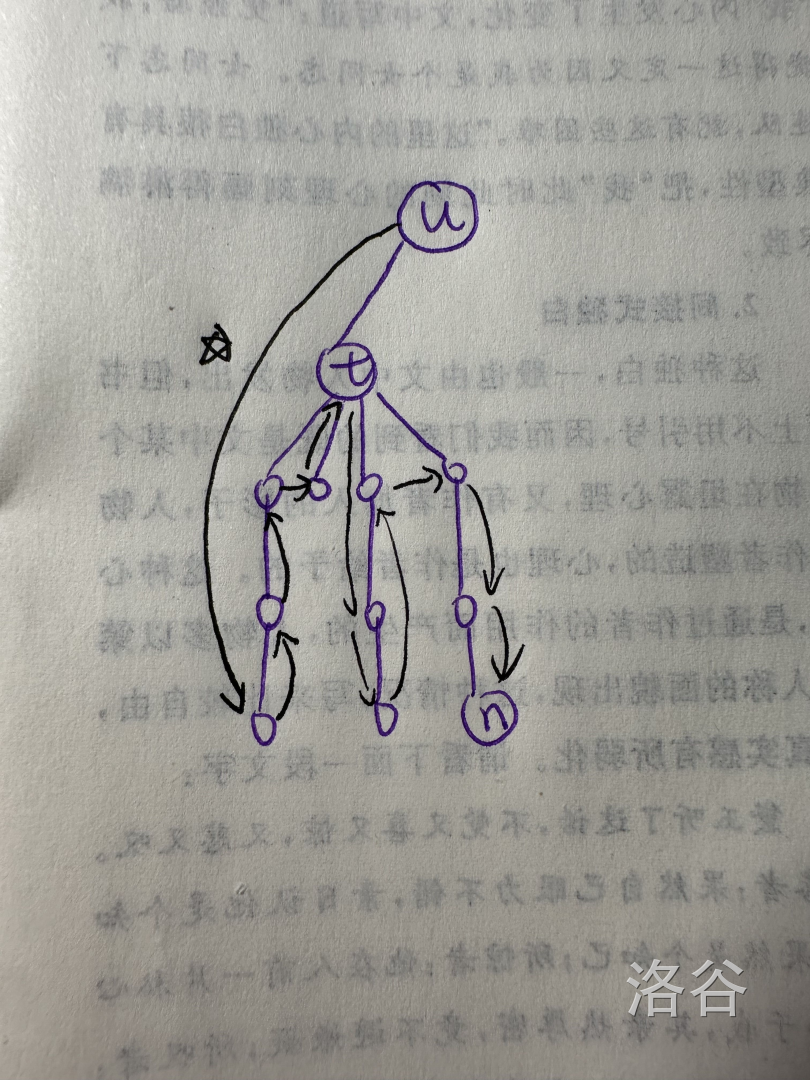
\(t\) 本身有两个除 \(n\) 所在子树外的非平凡子树，如果直接 \(\text{solve(t)}\) 是无解的，但是如果我在 \(u\) 位置的就直接下降到 \(t\) 的某个非平凡儿子，再回到 \(t\)，就能构造出一条合法的路径。

其实这个操作的本质就是“如果目前这个点有且仅有终点所在子树这一个儿子，我可以提前处理掉这个儿子的（除终点所在子树之外的） 一个非平凡儿子 和 所有平凡儿子”，这样可能使得本身有 \(2\) 个（除终点所在子树之外的）非平凡儿子的子树变得只有一个非平凡儿子，可以继续。 当然也可以使得一个只有一个非平凡儿子的点变得只有终点所在子树这一个儿子，可以继续传递下去这个性质。

可以发现少一个非平凡子树和一些平凡子树一定是不劣的，所以直接提前处理掉对应子树，并打好标记删除掉就行了。

---

\(\text{6.代码实现}\)

以下是所用到两个构造的 简述：

\(\text{go(u)}：\)

 若 \(u\) 有不少于两个非平凡儿子则非法。

 若 \(u\) 没有非平凡儿子则直接遍历。

 若 \(u\) 有一个非平凡儿子 \(s\)，则先下降到 \(s\) 的平凡儿子（若没有则直接下降 到 \(t\)），在其之间跳跃后跳到 \(t\)，递归执行 \(\text{go(t)}\)。

回到 \(s\)，在那些 \(u\) 平凡的叶子之间跳跃。

\(\text{solve(u)}：\)

如果 \(u\) 有目前剩余的唯一儿子 \(t\)。

  \(t=n\) ，跳到儿子并遍历，若有超过一个非平凡儿子则非法。

  \(t\neq n\) 那么处理掉 \(t\) 的一个非平凡儿子 \(p\)，执行 \(\text{go(p)}\) 后执行 \(\text{solve(t)}\)（如果没有则直接执行）。

\(u\) 有别的非平凡儿子 \(s\)，执行上面 \(\text{4}\) 中提到的

先下降到 \(s\) 的一个平凡儿子并在其之间跳跃访问完，再访问 \(s\) 的非平凡儿子 \(p\)（若没有则直接访问平凡儿子后返回），并对其执行 \(\text{go(p)}\)，结束后在 \(p\) 的某个儿子（若没有则直接返回），可以跳到 \(s\)，然后再跳到 \(u\) 的其它平凡儿子并在之间跳跃，最后访问 \(t\)，递归执行 \(\text{solve(t)}\)。

如果 \(n\) 有其它没有被消去的兄弟导致它只能被从兄弟跳跃过来，那么如果它有儿子就无法被访问了，无解。

---

贴坨屎在这里。感觉没什么参考价值。