【题解】CF319D | 字符串 哈希 观测点检测

CF319D Have You Ever Heard About the Word

好题，涉及复杂度分析，字符串结论，思维量较大。

发现这种操作是不好同时进行的，我们只能较为“愚蠢”地模拟着操作，但是这种操作最多又有可能有 \(O(n)\) 次，直接做的复杂度是 \(O(n^2)\) 的，但是能过，考虑优化，一个比较好想到的优化是把所有长度为 \(len\) 的 \(\text{XX}\) 一起缩，

首先若我们从小到大所掉了所有长度为 \([1,i-1]\) 的串后，接着缩完长为 \(i\) 的串后不可能存在长为 \([1,i]\) 的 \(\text{XX}\) 串可以再被缩，证明如下：

反证，假设缩完 \(\text{XX}\to \text X\) 后有连续串 \(\text{YY}\)，且 \(|Y|<|X|\)：

若 \(\text{YY}\) 有超出 \(\text X\) 的部分，则会直接缩掉 \(\text{YY}\)，不符合。

\(\text{X}\) 是 \(\text{YY}\) 的子串，则一定可以选取 \(\text{Y}\) 的一个子串使得它又是 \(\text{X}\) 的前缀又是 \(\text{X}\) 的后缀，所以 \(\text{XX}\) 的拼接处一定存在一个长度小于 \(\text X\) 的重复没有删除，不符合。

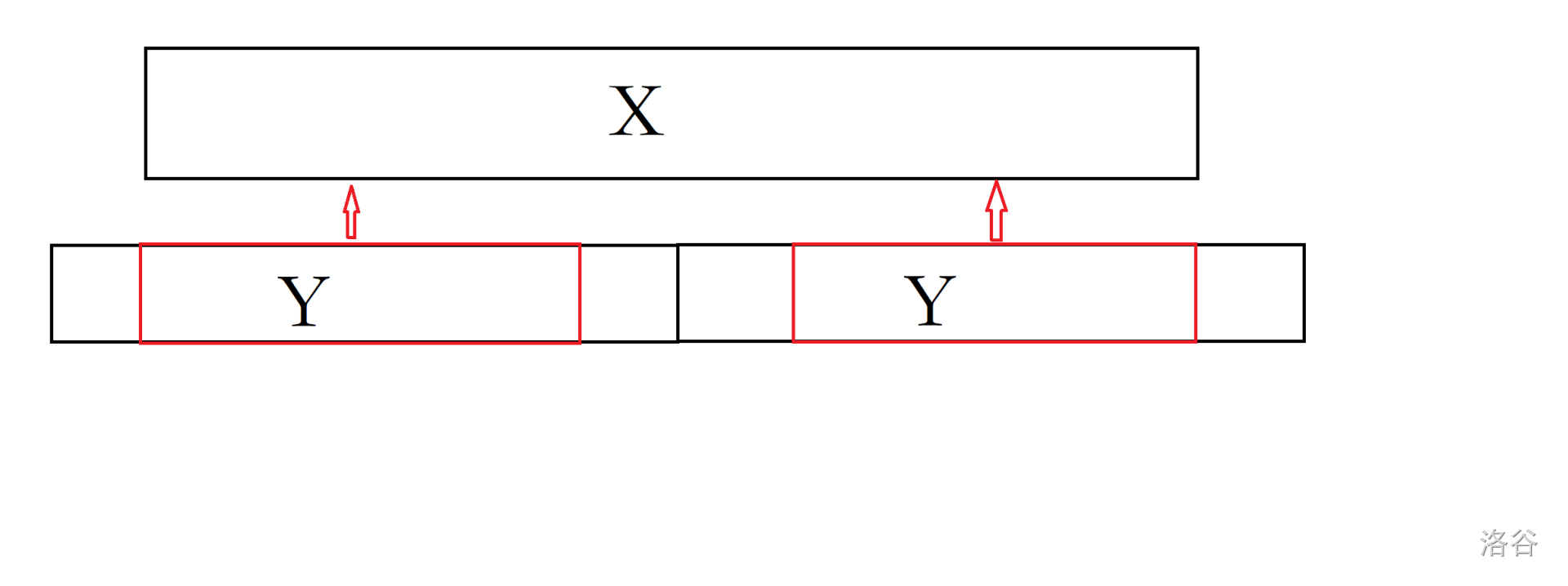
所以上述引理得证。

然后就证明了一件事：从小到大缩掉所有长度为 \(len\) 的串是正确的，长度为 \(len\) 的串是可以通过字符串算法或者相关技巧做到一次缩完，我们稍后讨论。

因为缩掉长度 \(2len\) 的 \(\text{XX}\) 后长度会减少 \(len\)，又因为总长是 \(n\)，所以所有串串最多有 \(\lceil 2 \sqrt n \rceil\) 种不同的长度，因为 \(1+2 \dots \lceil 2 \sqrt n \rceil \geq n\) 。

所以我们每次遇到能删的串串直接遍历全串删就完了，接下来我们要考虑如何判断是否存在 \(len\) 的 \(\text{XX}\) 串，用一个比较经典的套路就是将串分成长度为 \(len\) 的段，如果某段和前面的 LCP 和 后面段的 LCS 的长度之和不小于 \(len\)，那么一定存在一个这样的串，暴力缩长度为 \(len\) 的串，使用双指针或者哈希均可。

这样的观察点总数是 \(\sum _{len=1}^{n/2} \frac n {len}=O(n\log n)\) 。

然后我们需要一个快速求 LCS、LCP 的算法，设其初始化复杂度为 \(O(A)\)，单次查询复杂度为 \(O(B)\)，则总复杂度为 \(O(A\sqrt n + Bn\log n)\)，在这里使用字符串哈希的 \(A=n,B=\log n\) 优于后缀数组的 \(A=n\log n,B=1\)，总复杂度 \(O(n\sqrt n+n\log^2n)\)。