【题解】AGC059C 思维 图论 计数

Orz 蜜蜂！蜜蜂的智慧是不可估量的！

把偏序关系看作有向图上的边可以得到图 \(G\)。

一个条件 \((x,y)\) 是没用的当且仅当 \(G\) 中已经有 \(x\to y\) 或 \(y \to x\) 的链了。

直接判断两个点之间没有长度较大的链的方案数并且还要加入边，是不太现实的，思考了一会感觉不行，于是考虑约化出较强的条件：

因为最终给出的是一个全序集，而不是问“在某个条件处不合法”的排列，所以若某个条件 \(x \to y\) 有着一条很长的链，那么在之后连接这条链上的两个节点一定也不合法。

\(\text{assertion}:\) \((x,y)\) 不存在长度为 \(2\) 的链是排列全局合法的充分必要条件。

如果假设 \(x\to y\) 存在链 \(L\) 且长度大于 \(2\)，若 \(L\) 上存在两个距离为 \(2\) 的点之间还没有出现有向边，则后来出现的这条有向边不合法

试图构造出一条长度大于 \(2\) 的 链，且其中距离为 \(2\) 的点两两有有向边发现长度为 \(3\) 的链无法构造出：长度假设已经有了长度为 \(2\) 的链（图中的 \(1\to2\to3\)），现在加入点 \(4\) 。

此时 \(1\to 4,2\to 4,3\to4\) 产生了石头剪刀布的环形限制关系。

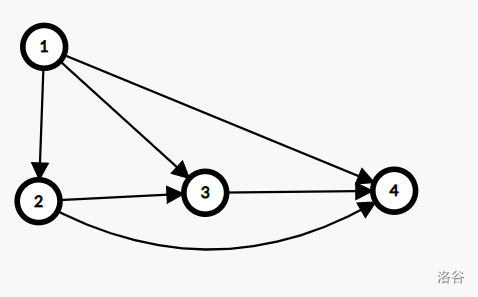
更长的满足条件的链也无法构造出，因为长度为 \(3\) 的链是它的一个子集。

所以条件就被强化为了只用考虑 \(x\to p \to y\) ， 也就是说 \(x \to y\) 限制了 \((x,p),(p,y)\) 不能同时存在。

直接处理出条件之间的相互限制关系，使用带权并查集或是直接 dfs 一遍即可判断可行性，由于每个联通块决定第一个条件的真假后就可以决定剩下条件的真假了，所以答案就是 \(2^k\) ， \(k\) 为联通块个数，时间复杂度 \(O(n^3)\) 或 \(O(n^3 \alpha(n^2))\)。

你可能会担心这样会不会答案的有向图连出环产生不合法的情况 ，仔细思考可以发现，限制边的方式决定了图上的“环”一定会被至少一条反向边“打断”，否则一定不合法。

code

让人恶心的是，atc 对 \(998244353\) 取模不是已成习俗了吗，咋搞 \(10^9 + 7\) 了？ 蜜蜂是不是 cf 混久了。