【题解】ARC153E Deque Minimization 卷积优化dp 组合转化

神仙题。

首先考虑 Minimization 的策略，假设现在队首为 \(f\), 如果加入的数 \(Y_i < f\)，放在队首是绝对更优的，如果 \(y_i=f\)，又因为这个数从前面放入的部分显然是不减的，所以放入一个新的相同的字符是不劣的。

计算 \(X\) 的数量，相当于我们需要计算合法的 LR 序列数，但有和队首相同且整个序列都相同时 L 和 R 是等价的，所以钦定和队首相同时放到前面。

最开始的想法是：考虑枚举前面和后面放入的分界点，然后把单增的前半部分和后半部分“交叉”起来，使得每个放入后面的数都严格大于放入前面的，后来发现这样无法做到低于 \(O(n^2|S|)\) 的复杂度，有很多东西被求出了很多次，没法继续下去了。

考虑一个信息利用效率高的做法——dp，令 \(f[l,r]\) 表示 \(Y[l,r]\) 可能对应的 \(X\) 的个数，那么有转移：

\[f[l,r]\to f[l,r+1] \quad (Y_{r+1} > Y_l) \]

\[f[l,r]\to f[l-1,r] \quad (Y_{l-1}\leq Y_l) \]

于是我们可以 \(O(n^2)\) 地解决这个问题了，考虑优化：

是发现很多状态是没有用的，比如对于串 \(\texttt{1234543333332}\) 来说，\(f[6,x]\) 都是没用的，因为结合我们前面说的，从前面插入的串一定是一个不降的串，这些状态显然无法转移到 \(f[1,n]\)，同样地，\(f[5,7]\) 也是无用的，因为 \(Y_r<Y_l\) 或 \(Y_r=Y_l\) 且不是只用一种数字组成的串都是不可能出现的。

因为这个转移只和 \(l,r\) 差 1 的相关，经典地，把 dp 状态看作一个网格，\(f[l,r]\) 看作点 \((l,r)\)，那么网格大概是这样的：

例串：\(\texttt{122455452}\)，有用的转移如下图：

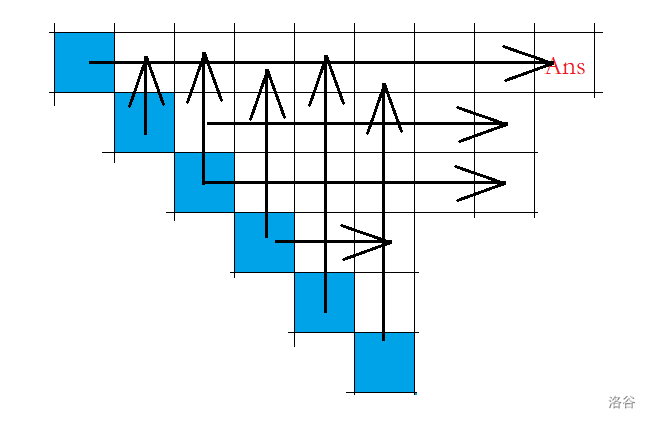
即：保留开头一段单调不减的行，然后对于每一个行，它的最右端为它这段的末端后第一个小于等于它的数，每种数的转移都是前面的只能向上，最后一列多出来的那部分才能向右走（即图中的 \((2,3),(3,3)\)，而 \((2,2)\) 不能。），求所有蓝色格子到 \((1,n)\) 的路径条数之和。

因为字符集大小 \(|S|=9\)，所以这个“阶梯”最多有九层，每层都形如下面这个形状：

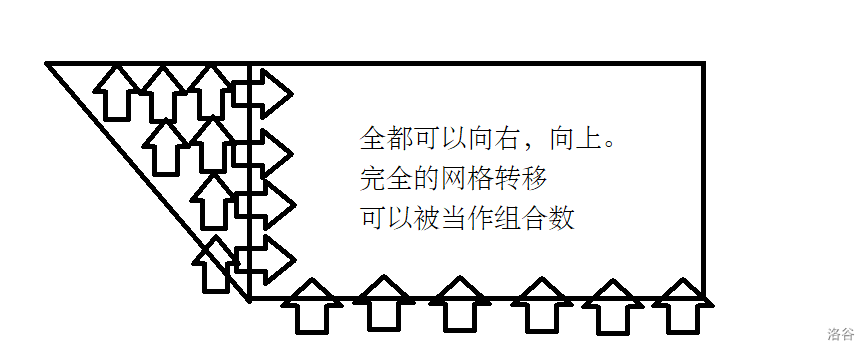
因为这个形状的性质，左边那个三角形上方的那些点都是 \(1\)，总共又只有 \(9\) 个阶梯，于是考虑从下往上处理每一个阶梯，并将结果代入下一个阶梯，

假设这个阶梯高 \(len\)，从原本的位置 \(i\) 走到新阶梯开头的位置 \(j\) 的方案数是 \(\binom {j-i+len}{len}\)， 容易发现这是一个卷积形式，即给原式的那个长方形对应的段乘上一个 \(g(x)=\binom{i+len}{len}\times x^i\)，再将三角形的底部赋为 \(1\)，传给下一个阶梯就可以解决了。

使用 NTT 进行卷积的运算，时间复杂度 \(O(|S|n\log n)\)。

代码：

实现很短，使用了 atcoder 库中的 modint998244353 类和 convolution 函数。

#define Z atcoder::modint998244353
#define poly vector<Z>
signed main()
{
init( ) ;
read(s) ;
n = strlen(s);
Z unit = 1 ,zero = 0;
int lim = n ;
for(int i = 1 ; i < n ; i ++) {
if(s[i]<s[i-1]){lim = i;break;}
}
poly scan(n,zero);
fill(scan.begin( ),scan.begin()+lim,unit);
for(char c='9';c>='1';--c) {
lb=tr=rb=-1;
for(int i = 0 ; i < n ; ++ i) if(s[i] == c) {lb = i;break;}
tr = lb ; while(tr+1<n&&s[tr+1]==c) tr++;
rb = tr + 1 ; while(rb<n&&s[rb]>c) rb++;
if(lb==-1||lb>=lim) continue ;
// [lb,rb)是有值的区间
poly tf,tg;tf.clear() , tg.clear() ;
for(int i = 0 ; i < rb - tr ; ++ i) {
Z x ; x = C( tr - lb + i , i ) ;
tg.emplace_back( x );
}
for(int i = tr ; i < rb ; ++ i) {
tf.emplace_back(scan[i]);
}
poly co = convolution(tf , tg) ;
for(int i = tr ; i != rb ; ++ i) scan[i] = co[i - tr] ;
for(int i = lb ; i < tr ; ++ i) scan[i] = 1 ;

}
cout << scan[n-1].val( ) ;
return 0;
}

---

参考了 AtCoder 原题解。

收录于《超级无敌神仙炫酷无敌原神大王好题》 。