【题解】Segment Covering 数据结构 ad-hoc 结论

首先直接求 \(f,g\) 是不可做的。 考虑这个奇偶差的性质。

若方案唯一，则答案为 1 或 -1。

若方案不唯一：

若存在着一些线段之间有着包含关系，则选择了大线段，是否选择被包含线段都是合法的，这也对应着不同的奇偶性，也就是说着这种情况对奇偶差是没有贡献的，于是我们删掉所有包含其它线段的线段。

则现在的线段排序后的 \(r\) 是随着 \(l\) 增加而增加的。

还有哪些线段在这种情况下对奇偶差是没有贡献的？

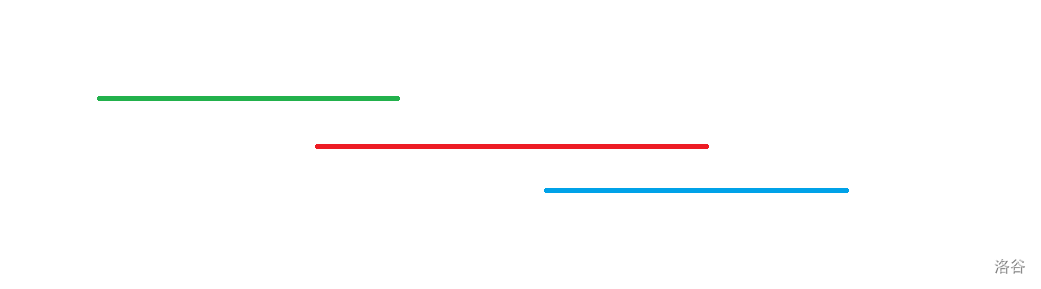
像这样，则有唯一的选择方法使得并集合法，答案是 1 或 -1 。

若存在这种下图中红线这样的线段：

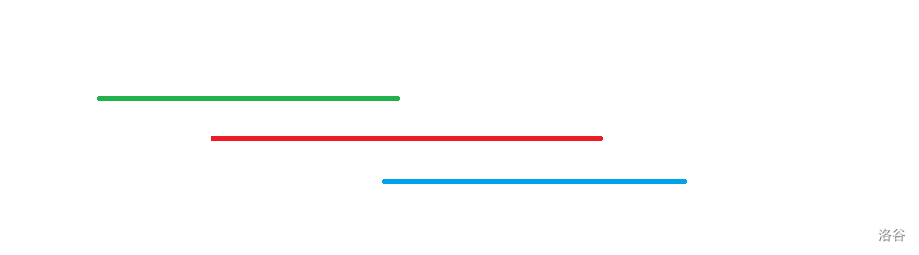
即被相邻两条线段的并包含。

则选蓝色线段后无论是否选取红色线段，都合法，对奇偶差无贡献。

也就是说最终那些有贡献的线段大概是长这样的：

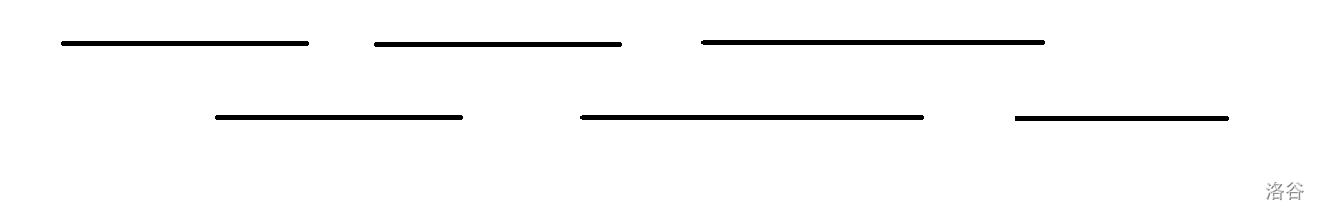
第一条线段和第三条交集为空，第二条和第四条交集为空 …… 这样下去。

于是现在就有了 \(O(nq)\) 做法：

先删去所有包含关系的线段，再把所有 \([l,r]\) 中的线段拿出来，删去所有上图中红色线段那样的线段，然后判断剩下的线段是否形成一种覆盖以及奇偶性。

考虑优化 ： 我们并不需要考虑“删去”的线段，我们只需要考虑那些保留的线段，而不是哪些线段被删去了。

对于每条线段，我们要找的其实是后面第一条与它不交的线段，从上图可以清晰看出。

那么我们找到第一条，第二条线段，并分别往后一直找下去就可以找到这些有用的线段，若出现了没有被覆盖的点，则第一条和第二条线段会跳到同一条线段上。

找下一条线段的过程可以使用倍增优化，时间复杂度 \(O(q\log n)\)。

下面是代码实现，有以下细节需要判断：

没有 \(l\) 开头的线段。

没有 \(r\) 结尾的线段。

第二条线段和第一条线段不交。

第二条线段超出了 \(r\)。

代码 (实现较为复杂，在 CF 最优解第一页。)