第十八届同济大学程序设计竞赛暨高校网络友谊赛
A（dfs）
题目链接
⭐
解析：
直接使用dfs，模拟他的他的判断过程即可。注意用一些trick，可以将节点进行重编号（使得叶子节点按照满二叉树先序遍历的顺序进行编号），如果某个节点\(a\)是另一个节点\(b\)的祖宗节点，则\(a\)一定是\(b\)的前缀，这样就可以去判断是否有冲突
注意：
- 尽管探索右儿子时可能已经分配完所有信道，但还是要添加这次查询次数
- 同时这道题可以进行优化，对于每个祖宗节点\(cur\)，二叉树还剩下\(x\)层他后代的叶子节点范围是可以计算的（\([cur\times2^x,(cur+1)\times2^x-1]\)），这样就可以对\(dat\)数组进行二分查询，复杂度从\(O(n^2)\rightarrow O(nlog(n))\)
#include<bits/stdc++.h>
using namespace std;
int n, k;
const int maxn = 5000;
int dat[maxn];
int dfs(int cur, int x) {
int cnt = 0;
for (int i = 0; i < k; ++i)
if (dat[i] >> x == cur) ++cnt; //trick
if (cnt <= 1) return 1;
return dfs(cur << 1, x - 1) + dfs(cur << 1 | 1, x - 1) + 1;
}
int main() {
scanf("%d%d", &n, &k);
for (int i = 0; i < k; ++i)
scanf("%d", &dat[i]), dat[i] += n - 1;
printf("%d", dfs(1, log(n) / log(2)));
}
C（dp or 组合数学）
题目链接
⭐⭐
解析：
- 第一种做法（dp） 复杂度\(O(n)\)
定义\(dp[i]\)为\(i\)被拆分的方案数，那么对于任意一个数\(i\)，考虑他的最后一项可以为任意数\(x（k\le x\le i\)，那么就不难得到状态转移方程\(dp[i]=\sum_{x=k}^idp[i-x]\)，注意到任意一个数都可以由它自己直接构成，所以\(dp[0]=0\)。且状态转移方程由于与区间连续和有关，所以可对dp数组的前缀和进行维护，进行\(O(1)\)查询
注意：
进一步优化发现可以将前缀和数组与\(dp\)数组合并
#include<bits/stdc++.h>
using namespace std;
const int maxn = 55;
int dat[maxn];
int main() {
int T, n;
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
bool ok = true;
for (int i = 0; i < n; ++i) {
scanf("%d", &dat[i]);
if (i && dat[i] < dat[i - 1]) ok = false;
}
if (ok) printf("0\n");
else {
if (dat[0] == n && dat[n - 1] == 1) printf("3\n");
else if (dat[0] == 1 || dat[n - 1] == n) printf("1\n");
else printf("2\n");
}
}
}
- 第二种做法（组合数学） 预处理复杂度\(O(n)\)，算法复杂度\((O(\lfloor\frac{n}{k}\rfloor))\)
考虑利用组合数学的思想解题，先有引理，对于一个\(n\)个木棍，分成\(x\)堆（每堆至少有1个），总共有\(C_{n-1}^{x-1}\)种方案（插空法），那么对于这道题就相当于变形题，既可以先在每堆种放置\(k-1\)个，再按引理的方式继续拜访，那么最后答案就是对各种分堆个数方案数的和
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
const long long mod = 1e9 + 7;
long long inv[maxn], jc[maxn];
long long q_pow(long long a, long long b) {
long long ans = 1;
while (b) {
if (b & 1) ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
typedef long long ll;
ll C(int n, int m) {
return jc[n] * inv[m] % mod * inv[n - m] % mod;
}
int main() {
ll n, k;
scanf("%lld%lld", &n, &k);
inv[0] = inv[1] = jc[0] = jc[1] = 1;
for (int i = 2; i <= n; ++i)
jc[i] = jc[i - 1] * i % mod;
inv[n] = q_pow(jc[n], mod - 2);
for (int i = n - 1; i; --i)
inv[i] = inv[i + 1] * (i + 1) % mod;
int end = n / k;
ll ans = 0;
for (int i = 1; i <= end; ++i) {
ans = (ans + C(n - i * (k - 1) - 1, i - 1)) % mod;
}
printf("%lld", ans);
}
D（思维）
题目链接
⭐⭐
解析：
好像就是之前cf的一道原题，由于时刻要保证区间内\(0,1\)的数量相等，所以相隔\(k\)个距离的字符也必须相等，因此在保证字符串可以满足上述条件的基础上，再去观察前\(k\)个字符是否可以满足\(0,1\)的数量相等
#include<bits/stdc++.h>
using namespace std;
int n, k;
const int maxn = 1000000 + 5;
char str[maxn];
void no() {
printf("No");
exit(0);
}
void yes() {
printf("Yes");
exit(0);
}
int main() {
scanf("%d%d", &n, &k);
scanf("%s", str);
if (k & 1) no();
int t[2] = { 0 };
int s = '0' + '1';
for (int i = 0; i < k; ++i) {
if (str[i] == '0' || str[i] == '1') {
++t[str[i] == '1'];
for (int j = i; j < n; j += k)
if (str[j] == s - str[i]) no();
}
else {
char c = 0;
for (int j = i; j < n; j += k)
if (!c && str[j] != '?')
c = str[j];
else if (c && str[j] != c) no();
if (c)
++t[c == '1'];
}
}
if (t[1] > k / 2 || t[0] > k / 2) no();
yes();
}
F（线性DP）
题目链接
⭐⭐
解析：
在如果没有要求第一个和最后一个珠子互相邻近的情况下，可以很容易定义\(dp[i][j]\)代表到第\(i\)行，选择\(j\)颜色的珠子时的最大价值
所以问题转化成了如何解决相邻的问题。可以通过指定开始珠子的颜色为红色，或者为蓝色进行\(dp\)，这样就完美解决了问题
\[dp[i][0]=\max(dp[i-1][0],dp[i-1][1])+v\\
dp[i][1]=dp[i-1][0]+v\\
~\\
ans=\begin{cases}
\max(dp[n-1][0],dp[n-1][1]) &\text{if initial color is blue}\\
dp[n-1][0] & \text{if initial color is red}
\end{cases}
\]
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 10;
const ll INF = -2e17;
int T, w, n, m;
ll dp[maxn][2], a[maxn], v[maxn][2], ans;
int f(int x, int y) {
return x * m + y;
}
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m);
for (int i = 0; i < n; ++i) {
v[i][0] = v[i][1] = INF;
for (int j = 0; j < m; ++j) {
scanf("%lld", &a[f(i, j)]);
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
scanf("%d", &w);
v[i][w] = max(v[i][w], a[f(i, j)]);
}
}
if (n == 1) {
printf("%lld\n", max(v[0][0], v[0][1]));
continue;
}
dp[0][0] = v[0][0];
dp[0][1] = INF;
for (int j = 1; j < n; ++j) {
dp[j][0] = max(dp[j - 1][0], dp[j - 1][1]) + v[j][0];
dp[j][1] = dp[j - 1][0] + v[j][1];
}
ans = max(dp[n - 1][0], dp[n - 1][1]);
dp[0][1] = v[0][1];
dp[0][0] = INF;
for (int j = 1; j < n; ++j) {
dp[j][0] = max(dp[j - 1][0], dp[j - 1][1]) + v[j][0];
dp[j][1] = dp[j - 1][0] + v[j][1];
}
ans = max(ans, dp[n - 1][0]);
printf("%lld\n", ans < 0 ? -1 : ans);
}
return 0;
}
G（最小费用最大流）
题目链接
⭐⭐
解析：
非常典型的最小费用最大流的模板题，构建超级源点连接有空余车的城市，构建超级汇点连接缺车的城市，直接跑就行了
#include<bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
namespace MinCostMaxFlow
{
const static int MAXN = 1000;//node
const static int MAXE = 10000;//edge
struct Edge
{
int from, to, next, cap, flow;
long long cost;
Edge() {}
Edge(int u, int v, int c, int f, long long _c, int nxt) :from(u), to(v), cap(c), flow(f), cost(_c), next(nxt) {}
}edge[MAXE];
int head[MAXN], tol, N, start, end;
int pre[MAXN];
long long dis[MAXN];
bool vis[MAXN];
//Function
void init()
{
N = MAXN;
tol = 0;
memset(head, -1, sizeof(head));
}
void link(int u, int v, int cap, int cost)//s->t,cap,cost
{
edge[tol] = Edge(u, v, cap, 0, cost, head[u]); head[u] = tol++;
edge[tol] = Edge(v, u, 0, 0, -cost, head[v]); head[v] = tol++;
}
bool spfa()
{
queue<int>Q;
for (int i = start; i <= end; i++) dis[i] = 0x3f3f3f3f3f3f3f3f;
for (int i = start; i <= end; i++) vis[i] = false;
for (int i = start; i <= end; i++) pre[i] = -1;
dis[start] = 0;
vis[start] = true;
Q.push(start);
while (!Q.empty())
{
int u = Q.front();
Q.pop();
vis[u] = false;
for (int i = head[u]; i != -1; i = edge[i].next)
{
int v = edge[i].to;
if (edge[i].cap > edge[i].flow && dis[v] > dis[u] + edge[i].cost)
{
dis[v] = dis[u] + edge[i].cost;
pre[v] = i;
if (!vis[v])
{
vis[v] = true;
Q.push(v);
}
}
}
}
if (pre[end] == -1) return false;
else return true;
}
int MCMF(long long& cost)
{
cost = 0;
int maxflow = 0;
while (spfa())
{
int Min = INF;
for (int i = pre[end]; i != -1; i = pre[edge[i ^ 1].to])
Min = min(Min, edge[i].cap - edge[i].flow);
//MIN=min(Min,goal-maxflow);
for (int i = pre[end]; i != -1; i = pre[edge[i ^ 1].to])
{
edge[i].flow += Min;
edge[i ^ 1].flow -= Min;
cost += edge[i].cost * Min;
}
maxflow += Min;
// if(maxflow==goal) break;
}
return maxflow;
}
};
const int maxn = 500 + 5;
int dat[maxn];
int main() {
int T, n, m, a, b, c;
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m);
MinCostMaxFlow::init();
MinCostMaxFlow::start = 0;
MinCostMaxFlow::end = n + 1;
int tot = 0;
for (int i = 1; i <= n; ++i)
scanf("%d", &dat[i]), tot += dat[i];
while (m--) {
scanf("%d%d%d", &a, &b, &c);
MinCostMaxFlow::link(a, b, INF, c);
MinCostMaxFlow::link(b, a, INF, c);
}
if (tot % n) {
printf("-1\n");
continue;
}
tot /= n;
int top = 0;
for (int i = 1; i <= n; ++i) {
if (dat[i] > tot) MinCostMaxFlow::link(MinCostMaxFlow::start, i, dat[i] - tot, 0), top += dat[i] - tot;
else if (dat[i] < tot) MinCostMaxFlow::link(i, MinCostMaxFlow::end, tot - dat[i], 0);
}
long long cost = 0;
if (MinCostMaxFlow::MCMF(cost) != top)
printf("-1\n");
else
printf("%lld\n", cost);
}
}
J（SG函数+找规律）
题目链接
⭐⭐⭐⭐
解析：
可以构造一个新的子游戏，子游戏可以在树上任意一点下棋，这样根据SG定理，答案就成了连接在根节点（1号节点）上平行子游戏的异或和
对于子游戏的SG值，简单画了几个树形进行\(mex\)操作可以发现，任一游戏的SG值等于以他为根节点的子游戏SG值得异或加1（具体证明待补...）
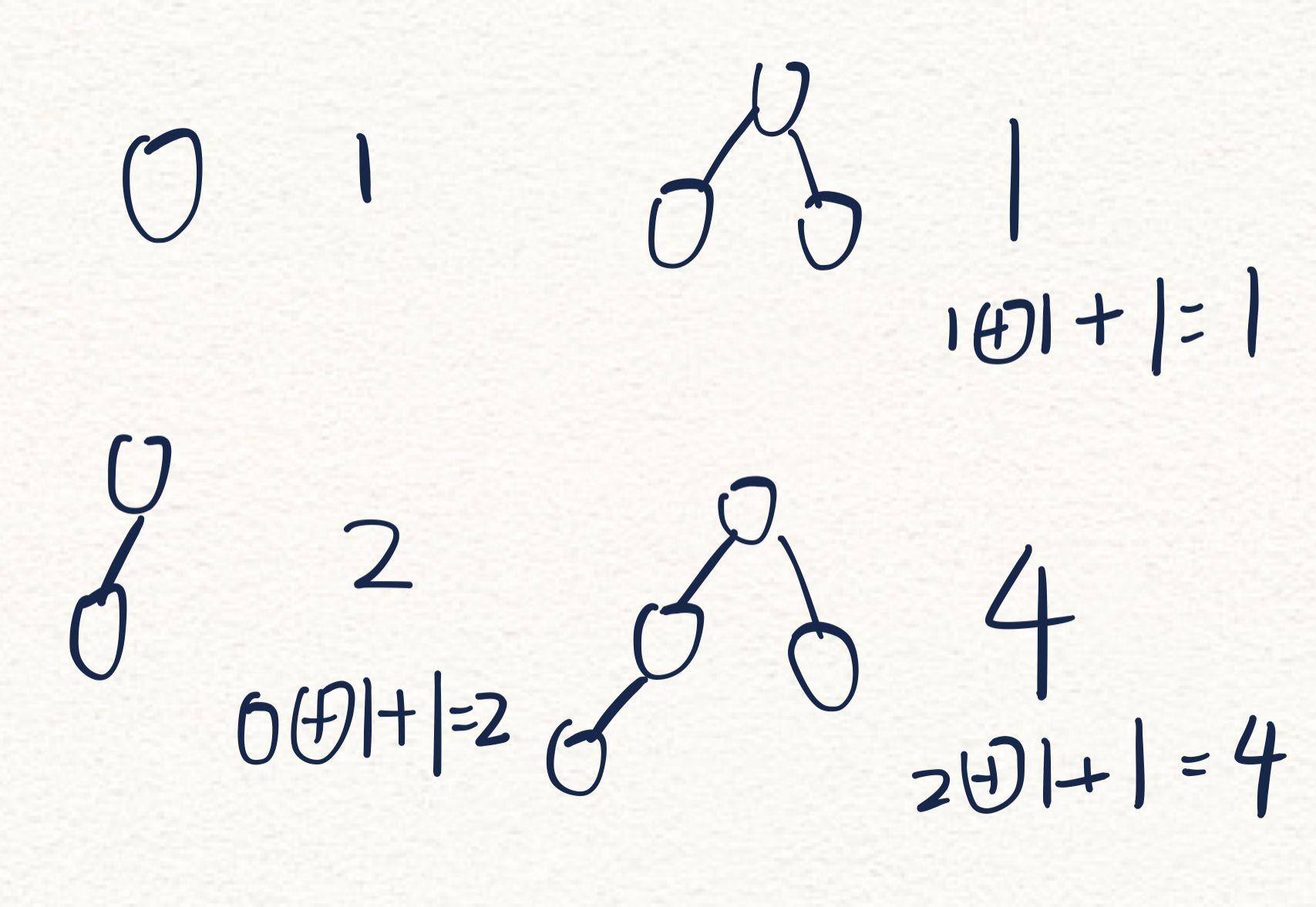
#include<bits/stdc++.h>
using namespace std;
int n;
const int maxn = 1e5 + 5;
vector<int> e[maxn];
int get_sg(int cur, int fa) {
int t = 0;
for (auto& i : e[cur])
if (fa != i)
t ^= get_sg(i, cur);
return t + 1;
}
int main() {
int T, a, b;
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) e[i].clear();
for (int i = 1; i < n; ++i) {
scanf("%d%d", &a, &b);
e[a].push_back(b), e[b].push_back(a);
}
int ans = 0;
for (auto& i : e[1])
ans ^= get_sg(i, 1);
printf("%s\n", ans ? "NO" : "YES");
}
}
努力变成更好的自己吧！
