Codeforces Global Round 13
A(水题)
题目链接
⭐
题目:
给出一个\(01\)序列,有2种操作:1.将某个位置取反;2.询问\(01\)序列中第\(k\)大的数
解析:
显然维护1的数目即可
#include<bits/stdc++.h>
using namespace std;
/*===========================================*/
int ones = 0;
const int maxn = 1e5 + 5;
int dat[maxn];
int main() {
int n, q, a, b;
scanf("%d%d", &n, &q);
for (int i = 0; i < n; ++i)
{
scanf("%d", &dat[i]);
ones += dat[i];
};
while (q--) {
scanf("%d%d", &a, &b);
if (a == 1) {
--b;
if (dat[b])
--ones;
else
++ones;
dat[b] = 1 - dat[b];
}
else {
printf("%d\n", ones >= b);
}
}
}
B(贪心)
题目链接
⭐⭐
题目:
给出一张图,由\(n(n\le100)\)行(行从1开始编号),\(10^6+1\)列组成(列从0开始编号),在所给矩阵的每一行存在一个障碍,现在可以花费\(v\)使得障碍水平移动,\(u\)使得障碍竖直移动,问若要从\((1,0)\)可以到达\((n,10^6+1)\),最小花费是多少?
(题目所给障碍物水平移动范围不包含两端)
解析:
由于水平移动范围不包含两端,所以不会出现上下封闭的情况,那么只有一种情况下无法到达,即所有障碍形成一条连续线段,将图分割成左右两部分,在这样的情况下,分以下两种情况进行讨论:
- 如果这是一条笔直的线段,即障碍所在列全部相同,则考虑将相邻障碍物一个左移一个右移,或者将障碍物先水平移动再垂直移动到不同行,形成空缺
- 如果不是笔直的,那么在可以在线段斜线处水平移动一次或者竖直移动一次,形成空缺
#include<bits/stdc++.h>
using namespace std;
/*===========================================*/
int ones = 0;
const int maxn = 105;
int ob[maxn];
int main() {
int T;
int n, u, v;
scanf("%d", &T);
while (T--)
{
bool left = true;
scanf("%d%d%d", &n, &u, &v);
for (int i = 0; i < n; ++i)
scanf("%d", &ob[i]);
int last = 0;
bool equ = true, line = true;
for (int i = 1; i < n; ++i)
{
if (abs(ob[i] - ob[i - 1]) > 1)
{
line = false;
break;
}
if (ob[i] != ob[i - 1])
equ = false;
}
if (line) {
if (equ)
printf("%d", min(2 * v, u + v));
else
printf("%d", min(u, v));
}
else
printf("%d", 0);
printf("\n");
}
}
C(思维)
题目链接
⭐⭐⭐
题目:
给出\(n\)个蹦床,每个蹦床有一个强度\(S_i\),如果身处\(i\)蹦床,会跳跃至\(i+S_i\)处,且每次蹦床被踩压后,强度会\(-1\),但至多减至1,现在可以从任意位置起跳,每次跳跃直到无蹦床可以踩压为止,问将所有蹦床强度降至\(1\),所最少需要的游戏次数
解析:
- 假设从\(i\)蹦床出发,他只会对\(\ge i\)的部分产生影响,所以如果全要降为\(1\),则需要从前到后的遍历蹦床,并将其强度减到\(1\)为止
- 这就要求维护一个\(t\)数组,统计\(i\)之前的蹦床跳跃时对\(i\)的影响,显然仍需要跳跃的次数为\(\max(S_i-1-t_i,0)\)
- 将\(i\)位置的强度降为\(1\),则会踩压到\(i+2,i+3,...,i+S_i\)的所有蹦床,即所属\(t\)均要加\(1\)
- 同时也不难发现,可能由于受之前影响的踩压次数过多(未遍历到\(i\)以前,\(S_i\)已经降为\(1\)了),就可以传递给下一个蹦床,即\(t[i+1]=\max(t_i-S_i+1,0)\)
注意:
- 答案需要开\(long\ long\)存储
- 第\(i\)号蹦床对后序的影响,即\(+1\)过程,可以用差分数组维护
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e3 + 5;
int dat[maxn];
int t[maxn];
long long ret;
int main() {
int T,n;
scanf("%d", &T);
while (T--) {
ret = 0;
scanf("%d", &n);
for (int i = 0; i < n; ++i)
scanf("%d", &dat[i]);
memset(t, 0, sizeof(t));
for (int i = 0; i < n; ++i) {
int x = max(0, dat[i] - 1 - t[i]);
ret += x;
int end = min(n - 1, i + dat[i]);
for (int j = i + 2; j <= end; ++j)
++t[j];
t[i + 1] += max(t[i] - dat[i] + 1, 0);
}
printf("%lld\n", ret);
}
}
D(思维+位运算)
题目链接
⭐⭐⭐
题目:
规定如果\(u\&v=v\),则\(u\)可达\(u+v\),现在给出\(u,v\),问是否可以从\(u\)到\(v\)
解析:
- 如果\(u\rightarrow v\),则\(u<v\)是显然的
- 不难发现对于任意一个\(u\),对于所有\(u\)可达点的中间变量\(v'\),满足:\(v'\)中如果位数为1,则必有\(u\)中对应位也为\(1\),而\(u+v'\)可以使得\(1\)的位置向左移,如1101+0001=1110,且在\(1\)连续的情况下,可以选择性的消除任意个多余的\(1\),例如0111+0001=1000,或0111+0101=1100
- 那么对于所给出的\(u\)与\(v\)只要保证每个\(v\)的每一位的右边位置,\(u\)的\(1\)比\(v\)多,则就可以通过不断左移或消除\(1\),获得所需要的\(v\)序列。换句话说即每个\(v\)中,位为\(1\)的右边位上还含有若干个未被抵消(使用)的\(u\)的1
附:
- \(+v'\)操作肯定不会使得\(u+v'>v\)原因在于,对于每个\(v\)如果有1,则他的右边\(u\)存在很多1,这两段二进制代码的差一定是大于等于1的,如100000与0011010
- 如果当前\(u\)位也存在1,则可以将这些多余的1放在后续中被消除,这是一定能完成的。因为初始时保证\(u\le v\),如果二者\(1\)的数目不等,则必然存在\(v\)的一个最高位使得\(v\)中有\(1\),而\(u\)终没有
E(暴力+分治+树)
题目链接
⭐⭐⭐⭐⭐
题目:
规定\(Fib-tree\)必须满足以下条件
- 顶点数为\(Fibonacci数\)
- 只有一个顶点或者可以通过消除某条边将树分割成两个\(Fib-tree\)
现在给出树的边,问是否是一个\(Fib-tree\)
解析:
-
首先对顶点数进行判定是否为\(Fibonacci数\)
-
如若这个树可以分割成两个子\(Fib-tree\),则一定能肯定两个子树的顶点数为\(fib[k-1],fib[k-2]\),同时也可以证明,如果存在多条(最多两条,由树的定义可知)可以分割的边,则消除任意一条可行边不会影响结果
证明:如果存在两条边分割子树顶点数为\(fib[k-1],fib[k-2]\),如果使用某一条可行边将其分割,另一条可行边一定是在\(fib[k-1]\)对应的子树中,会将\(fib[k-1]\)分割为\(fib[k-2],fib[k-3]\),所以两条边是等价的
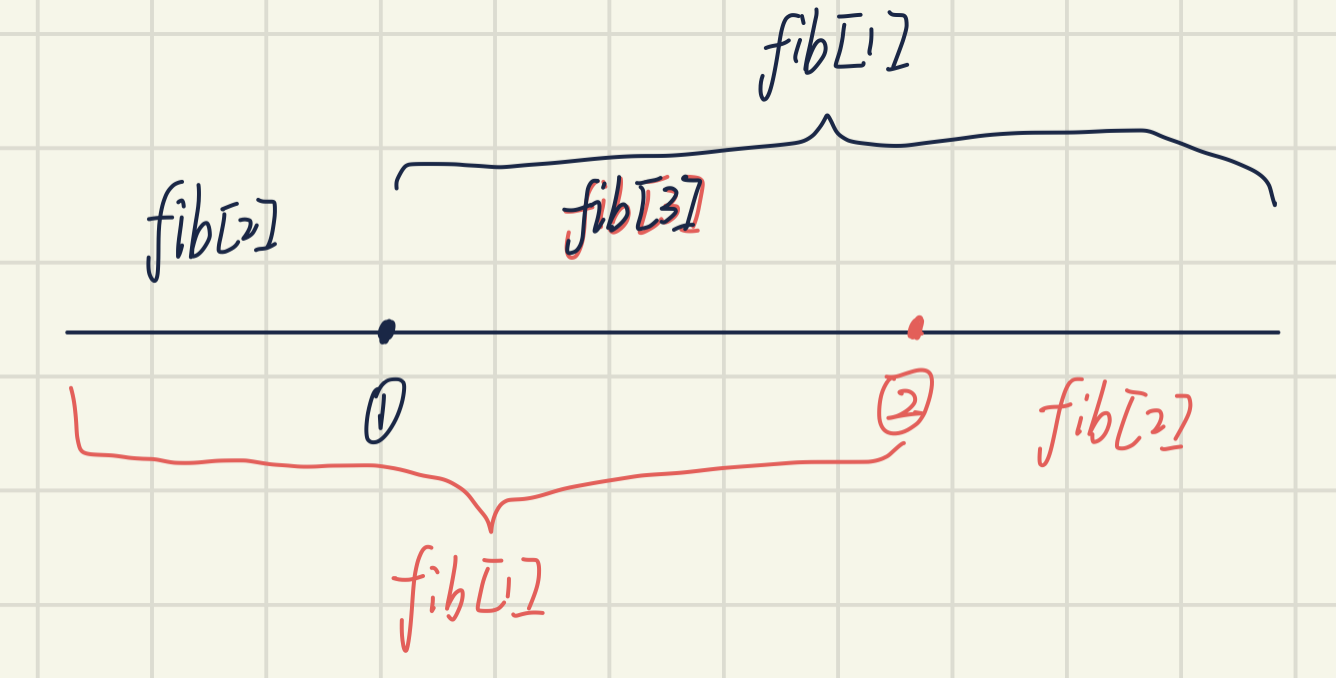
-
这样的情况下,构建一个\(getSize\)函数获取以某个点为根,子树的大小,如果子树大小为\(fib[k-1]\)或者\(fib[k-2]\)则考虑分割这条边,然后进行递归性的处理即可
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
vector<int> fib;
typedef pair<int, bool> P;
vector<P> e[maxn];
int siz[maxn];
int n;
void no() { printf("NO"); exit(0); }
void getSize(int u, int fa) {
siz[u] = 1;
for (auto& i : e[u]) {
if (i.second || i.first == fa) continue;
getSize(i.first, u);
siz[u] += siz[i.first];
}
}
void cutEdge(int u, int fa, int k, int& pu, int& pv, int& kd) {
for (auto& i : e[u]) {
if (pu) return;
if (i.second || i.first == fa) continue;
if (siz[i.first] == fib[k - 1] || siz[i.first] == fib[k - 2]) {
pu = u, pv = i.first;
kd = siz[i.first] == fib[k - 1] ? k - 1 : k - 2;
return;
}
cutEdge(i.first, u, k, pu, pv, kd);
}
}
void Check(int u, int k) {
if (k <= 1) return;
getSize(u, 0);
int pu = 0, pv = 0, kd = 0;
cutEdge(u, 0, k, pu, pv, kd);
if (!pu) no();
for (auto& i : e[pu])
if (i.first == pv) i.second = true;
for (auto& i : e[pv])
if (i.first == pu) i.second = true;
Check(pv, kd);
Check(pu, 2 * k - 3 - kd);
}
int main() {
int u, v;
scanf("%d", &n);
fib.push_back(1), fib.push_back(1);;
while (fib.back() < n)
fib.push_back(fib[fib.size() - 1] + fib[fib.size() - 2]);
for (int i = 1; i < n; ++i) {
scanf("%d%d", &u, &v);
e[u].push_back(P(v, false));
e[v].push_back(P(u, false));
}
if (fib.back() != n) no();
Check(1, fib.size() - 1);
printf("YES");
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号