在本章,我们学习了很重要的数据结构——图。
(1)图(GRAPH)的定义:是一种非线性数据结构,由有穷、非空的点集V(G)和边集E(G)组成。当G中的每条边有方向时,称G为有向图,有向边(用一对尖括号<a,b>)又称为弧,起始顶点被称为弧尾,终止顶点被称为弧头,每条边无方向时(用一对括号表示(a,b)和(b,a)一样),被称为无向图。
(2)图的存储方式:由于图的结构较为复杂,任意两个顶点之间都可能存在联系,因此无法用数据元素在存储区中的物理位置来表示元素之间的关系,但是我们可以借助一个二维数组中的各单元的数据取值或者多重链表来表示元素之间的关系
(1.图的邻接矩阵存储的结构:使用一个矩阵来表示各顶点之间的关系,A[i,j] = {0或1},表示顶点i到顶点j的连通性,有向图时为其权值,这样我们就可以使用一个二维数组加以表示
#define maxvex 100 typedef struct { char vexs[maxvex]; int arc[maxvex][maxvex]; int vertex,edges; }MGraph;
(2.无向图
#define maxvexs 100 #define infinity 65535//用65535来表示∞ typedef struct { char vexs[maxvexs]; int arc[maxvexs][maxvexs]; int vertexes,edges; }mgraph; void creatgraph(mgraph *g) { int i,j,k,w; printf("输入顶点数和边数:\n"); scanf("%d,%d",&g->vertexes,&g->edges); for(i=0;i<g->vertexes;i++)//读入顶点信息,建立顶点表 scanf("%c",&g->vexs[i]); for(i=0;i<g->vertexes;i++) for(j=0;j<g->vertexes;j++) g->arc[i][j]=infinity;//初始化邻接矩阵 for(k=0;k<g->vertexes;k++)//读入edges条边,建立邻接矩阵 { printf("输入边(Vi,vj)上的下标i,下标j,和权w:\n"); scanf("%d%d%d",&i,&j,&w); g->arc[i][j]=w; g->arc[j][i]=w;//无向图,矩阵对称 } }
(3.邻接表:数组与链表相结合的存储方法。
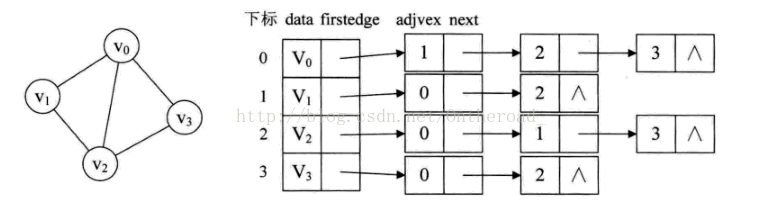
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域,存储权值信息即可。
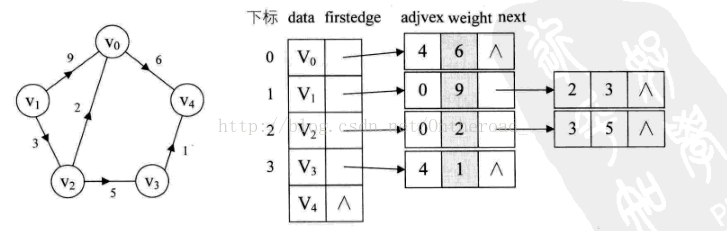
typedef struct EdgeNode { int adjvex; //邻接点域,存储该顶点对应的下标 int weight; //用于存储权值,对于非网图可以不需要 struct EdgeNode *next; //链域,指向下一个邻接点 }EdgeNode;//边表结点 typedef struct VertexNode //顶点表结点 { char data; //顶点域,存储顶点信息 EdgeNode *firstedge; //边表头指针 }VertexNode,AdjList[MAXVEX]; typedef struct { AdjList adjList; int numVertexes,numEdges;//图中当前顶点数和边数 }GraphAdjList;
最小生成树:
当使用一个连通网罗来构造生成树时,可以得到一个带权的生成树,把生成树各边的权值总和作为生成树的权,具有最小权值的生成树构成连通网络的最小生成树,构造最小生成树的两种常用算法:Prim算法和Kruskal算法;
最小生成树的MST性质:假设G=(V,G)是一个连通网络,U是V的一个真子集,若存在顶点u属于U和顶点v属于V-U的边(u,v)是一条具有最小权值的边,则必存在G的一颗最小生成树包括这条边(u,v)
图的遍历:使用辅助数组 visit[N] 表示顶点是否被遍历过,若已经被访问置1,未被访问置0
DFS:深度优先搜索:
从图中某一顶点出发,访问后标记visit[i]为1,然后依次搜索第i个结点的领接点j,再依次搜索j结点的每个领接点,直到所有结点都被遍历
BFS:广度优先搜索
先被访问的结点,其领接点也先被访问,具有先进先出的特性,我们使用队列来保存已经访问过的结点,以确定被访问过结点的顶点领接点访问次序。
生成树与最小生成树
树是一个无回路存在的连通图,而一个连通图G的生成树是指:一个包含了G的所有顶点的树。对于一个有n个顶点的连通图G,其生成树包含了n-1条边,从而生成树是G的一个极小连通的子图。使用DFS遍历搜索得到的树为DFS树,使用BFS遍历搜索得到的树为BFS树。
因为搜索算法选取的起始顶点不同,所以一个连通图的生成树不是唯一的,它取决于遍历方法和起始顶点的选择。
对于带权值的连通图,我们可以得到一个带权的生成树,我们将该生成树的各边的权值作为生成树的权,具有最小权值的生成树构成了连通网络的最小生成树
常用的最小生成树的算法有Prim算法和Krusal算法
最短路径问题:沿路径的各边权值之和最小。主要有两种算法:
Dijkstra算法:单源最短路径:求图中某个顶点到其他各顶点的最短路径
Floyd算法:各顶点间最短路径:每对顶点之间的最短路径
学习过程中有很多一开始理解不了的地方,比如图的最短路径问题,而且因为概念很多,有时候会混淆或者遗忘,两个算法也并没有完全掌握,利用图来解决问题的能力还是不足,所以还要多刷题多看代码多练习!!!





