算法分析设计(Dijstra算法)
1.问题
对于下图使用Dijkstra算法求由顶点a到顶点h的最短路径,按实验报告模板编写算法。
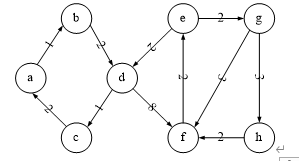
2.解析
第一点:

第二点:我们已经知道了起点s,一开始对于顶点s各个顶点的距离(用数组dis[j]表示s->j的距离),我们可以通过与顶点s相连的边得知。
假设顶点k,是距离顶点i最近的一个顶点(除去s本身),顶点j是除去i,k以外的一个节点
因此我们知道: dis[k] < dis[j]
再假设 dis[k] + path[k][j] < dis[j]
因此 如果我们先用顶点j去松弛其他边是没有意义的,因此dis[j]本身还是能够被松弛,所以通过dis[j]松弛得到的最短边并不是我们最优的解。
因此当dis[j]不能在被松弛的时候,说明此时dis[j]已经是s->j的最短距离,这是我们就可以用dis[j]来对其他边进行松弛操作。
那到什么时候dis[j]已经是最短了呢?
看回 dis[k] < dis[j]
可以推导出 dis[k] < dis[j] + path[j][k]
因此顶点j不能优化dis[k]
这里就可以得出结论了,当dis[j]为剩下的顶点中距离i最近的顶点式,必定可以通过顶点j对其他边进行松弛操作
3.设计

void Dijstra() { cin >> s; dis[s] = 0; for (int i = head[s]; i != -1; i = edge[i].next) //知道起点s后,可以对于以s为起点的边进行遍历,来更新dis的值 { dis[edge[i].v] = edge[i].val; que.push(node(edge[i].v, edge[i].val)); } while (que.size()) // 通过维护小顶堆,优化了每次需要寻找vis[i] == 0 && dis[i] 最小的过程 { node tmp = que.top(); // 每次取堆顶 ,即最小值 ,判断该顶点是否杯访问过,如果没有没访问过 ,则用该边作为中转点进行松弛操作 que.pop(); if (vis[tmp.v]) continue; vis[tmp.v] = 1; for (int i = head[tmp.v]; i != -1; i = edge[i].next) { int j = edge[i].v; if (dis[j] > dis[tmp.v] + edge[i].val) { dis[j] = dis[tmp.v] + edge[i].val; que.push(node(j, dis[j])); // 假如顶点j可以通过顶点tmp.v进行松弛操作,说明使用顶点j来进行松弛操作时,有更优的选择,因此把(j ,新的dis[j])加入到堆中 } } } } }
4.分析
时间复杂度:O(nlogn)
初始的Dijstra算法的时间复杂度是O(n^2),通过堆优化,可以logn的维护出边权的最小值,不用再通过O(n)的遍历来确定最小值。又因为有n个节点需要作为中转点来对其他边进行松弛操作,因此在堆优化之后Dijstra算法的时间复杂度就是O(nlogn)
空间复杂度:O(m + n)
通过链式前向星来维护边的信息,因此空间复杂度仅需要O(n + m)
5.代码

#include<iostream> #include<algorithm> #include<memory.h> #include<queue> #include<vector> using namespace std; const int maxn = 1e5 + 100; const int inf = 0x3f3f3f3f; struct node { int v, val, next; inline bool operator < (const node & a) const { return val > a.val; } node(int x, int y) { v = x; val = y; } node() {} }; node edge[maxn]; // edge存储边的信息 int head[maxn], cnt = 0; void addedge(int u, int v, int val) // 通过链式前向星存图能够有效地降低空间复杂度 { edge[cnt].val = val; edge[cnt].v = v; edge[cnt].next = head[u]; head[u] = cnt++; } int n, m ,s; // n 为顶点个数, m为边数 , s是起点 priority_queue<node>que; // 通过堆优化能够有效地减少时间复杂度 int dis[maxn], vis[maxn]; // dis维护从起点s到其他顶点地最段距离 , vis用来维护在进行算法过程中那先顶点已经作为中转点进行过松弛操作 void Dijstra() { cin >> s; dis[s] = 0; for (int i = head[s]; i != -1; i = edge[i].next) //知道起点s后,可以对于以s为起点的边进行遍历,来更新dis的值 { dis[edge[i].v] = edge[i].val; que.push(node(edge[i].v, edge[i].val)); } while (que.size()) // 通过维护小顶堆,优化了每次需要寻找vis[i] == 0 && dis[i] 最小的过程 { node tmp = que.top(); // 每次取堆顶 ,即最小值 ,判断该顶点是否杯访问过,如果没有没访问过 ,则用该边作为中转点进行松弛操作 que.pop(); if (vis[tmp.v]) continue; vis[tmp.v] = 1; for (int i = head[tmp.v]; i != -1; i = edge[i].next) { int j = edge[i].v; if (dis[j] > dis[tmp.v] + edge[i].val) { dis[j] = dis[tmp.v] + edge[i].val; que.push(node(j, dis[j])); // 假如顶点j可以通过顶点tmp.v进行松弛操作,说明使用顶点j来进行松弛操作时,有更优的选择,因此把(j ,新的dis[j])加入到堆中 } } } } int main() { cin >> n >> m; memset(vis, 0, sizeof vis); //初始化数组中的信息 memset(dis, inf, sizeof dis); memset(head, -1, sizeof head); for (int i = 1; i <= m; ++i) { int u, v, val; cin >> u >> v >> val; addedge(u, v, val); } Dijstra(); cout << "顶点s到其他顶点的距离:" << endl; for (int i = 1; i <= n; ++i) { cout << s << "->" << i << " " << dis[i] << endl; } return 0; } /* 样例输入: 8 11 3 1 2 1 2 1 2 4 2 4 3 1 5 4 2 4 6 8 5 7 2 6 5 2 7 6 3 8 6 2 7 8 3 1 */





 浙公网安备 33010602011771号
浙公网安备 33010602011771号