算法设计分析（Kruskal构造最小生成树）

问题：

给定无向图G（N，M）表明图G有N个顶点，M条边，通过Kruskal算法构造一个最小生成树

分析：

算法流程:

 

 

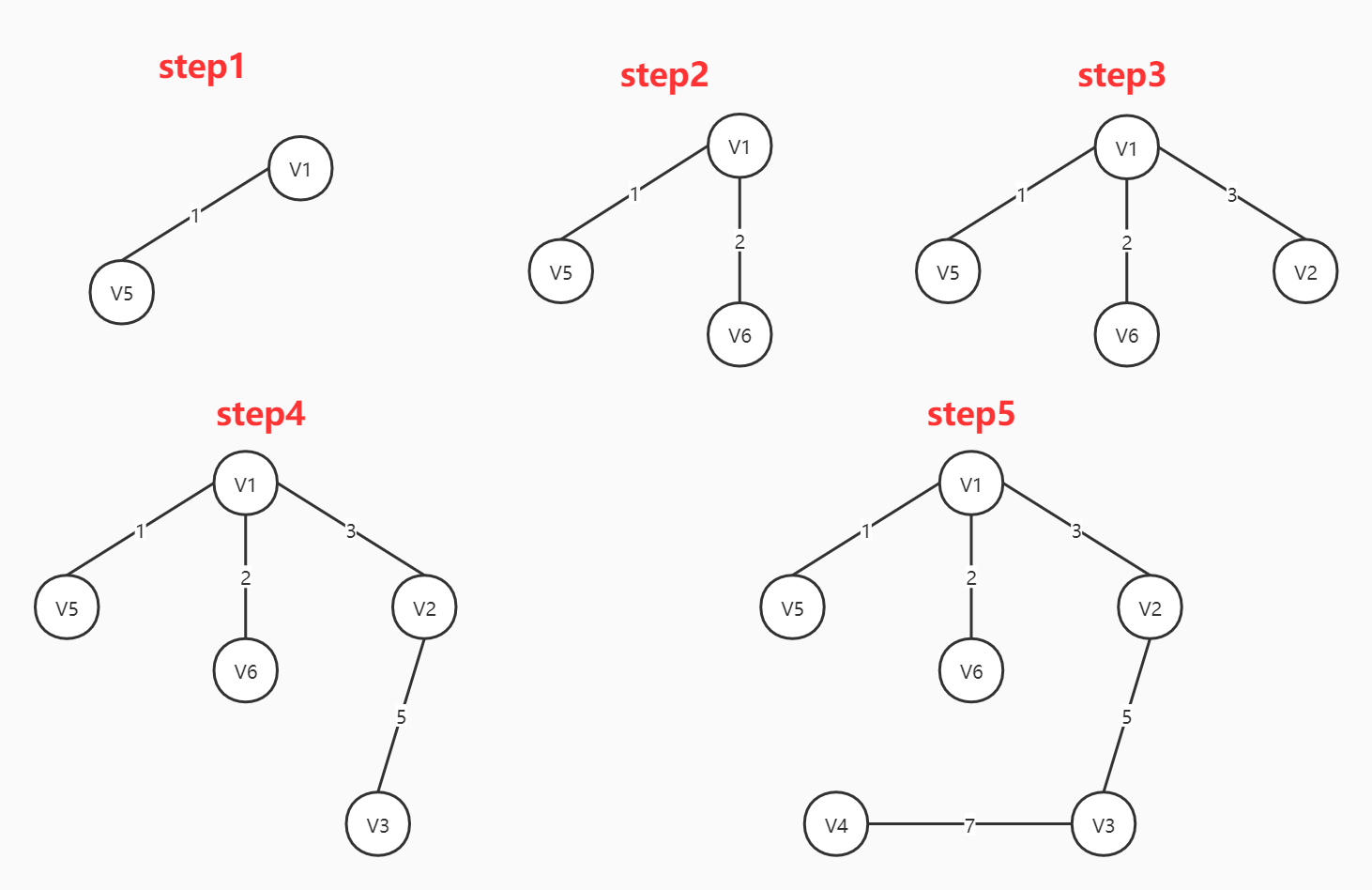
构造好的最小生成树就是step5

#include<cstdio>
#include<string.h>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<vector>
#include<queue>
#include<set>
#include<map>
#include<cctype>
#include<stack>
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define mem(a,x) memset(a,x,sizeof(a))
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid + 1,r
#define P pair<int,int>
#define ull unsigned long long
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 10;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-7;

int n, m;
struct node
{
    int u, v, val;
}edge[maxn],ansedge[maxn];                                //edge存边的端点u,v,以及边的权值val,ansedge维护构成最小生成树的边的信息
int  father[maxn];
int cmp(const node& a, const node& b)                            //对于边的权值大小进行排序    
{
    return a.val < b.val;
}
int find(int x)                                        //通过并查集算法来判断两个顶点是不是同属于同一棵树，可以查找这两个顶点的祖先是否相同，如果相同则说明两个顶点在同一棵树中
{
    return x == father[x] ? x : father[x] = find(father[x]);
}
void MergeTree(int x, int y)                                // 对于不同的两个，通过MergeTree来讲两个树合并成一棵树
{
    int fx = find(x) , fy = find(y);
    father[fx] = fy;
}

int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= m; ++i)
    {
        scanf("%d %d %d", &edge[i].u, &edge[i].v, &edge[i].val);
    }
    sort(edge + 1, edge + 1 + m, cmp);                        //对边的长度进行排序，在构造最小生成树中的过程中，权值较小的边其优先级总是高于权值大的边
    for (int i = 1; i <= n; ++i)
    {
        father[i] = i;
    }
    int cnt = 0;                                    //cnt记录用于构成最小生成树的边数，根据最小生成树的概念可知，满足条件的边数应该为顶点数-1
    int ans = 0;                                    //ans记录最小生成树的权值和
    for (int i = 1; i <= m; ++i)
    {
        if (cnt == n - 1) break;                        //如果构成最小生成树的边数已经为顶点数-1，那么最小生成树已经构建完成
        if (find(edge[i].u) != find(edge[i].v))                    //判断一条边的两个顶点是否在同一棵树中，如果在同一棵树中则该边为无效边，不能用于构造最小生成树
        {
            cnt++;                                //记录用于构成最小生成树的边数
            MergeTree(edge[i].u, edge[i].v);                //因为该边将两个不同的树进行了连接所以需要合并成一颗树
            ans += edge[i].val;                        //维护最小生成树的权值和
            ansedge[cnt] = edge[i];                        //维护构成最小生成树的边的信息
        }
    }
    printf("最小生成树的权值和为：%d\n", ans);
    printf("构成最小生成树的边为\n");
    for (int i = 1; i <= cnt; ++i)
    {
        printf("%d %d %d\n", ansedge[i].u, ansedge[i].v, ansedge[i].val);
    }
    return 0;
}