Container With Most Water和3Sum

〇、11. Container With Most Water 描述

Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

大意：给了你柱子的高度，你得找出哪两根柱子之间的面积最大

 

 

 

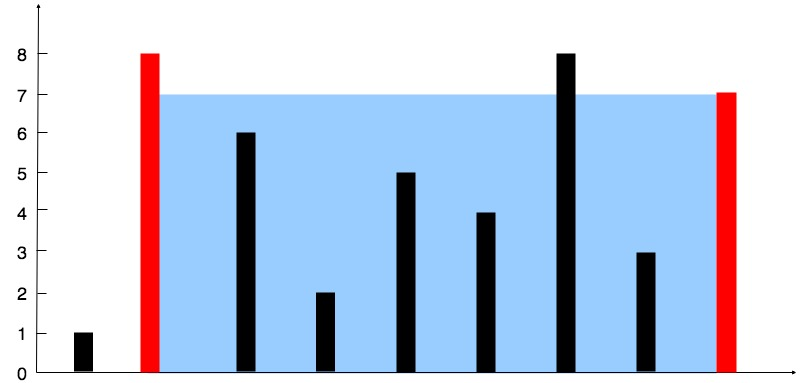
11. Container With Most Water  思路

1、暴力解：O(n²)的方法，每根柱子和其他的匹配，遍历完毕，找到最大。

2、两头逼近：

既然是求最大面积，我们当然想高尽量大、宽也尽量大。

从上图可以看出，依次找出两根最高、最高的与次高.....最终也会变成O(n²)的方法；

所以我们从'宽'入手，首先找距离最远的两根（即下标为0，和下标最后），选择矮的柱子为高，计算并记录面积；

然后两根柱子中，我们保留高的那一根，矮的一边则向中间逼近，直到两柱子相遇...并在此过程中比较得出最大值；

在选择最远距离->宽尽量大，保留高的一方->高尽量大。

class Solution(object):
    def maxArea(self, height):
        length = len(height)
        i = 0
        j = length-1
        max = 0
        while i<j :
            if height[i]>height[j] :
                max = height[j]*(j-i) if max<height[j]*(j-i) else max
                j -=1
            else:
                max = height[i] * (j - i) if max < height[i] * (j - i) else max
                i += 1
        return max

 

一、15. 3Sum 描述

Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

Notice that the solution set must not contain duplicate triplets.

example：
Input: nums = [-1,0,1,2,-1,-4]
Output: [[-1,-1,2],[-1,0,1]]

大意：给出一连串的整数，找出其中加起来等于0的三个元素（可能有0组或多组，且不能重复）

 

15. 3Sum 思路

我们可以固定一个元素，然后找其它两个元素，即  -a = b + c，这样就可以和11. Container With Most Water  差不多，采用两头（i，j）逼近方法。

但困难的地方在于  不能重复（像例子中，虽然有两个-1，但结果不能有两个[-1, 0, 1]，要保证组与组的数值不能完全同样）；

解决办法是跳过 已经判断的、重复的 元素；

小细节：三个元素和为0，所以其中要么正负搭配，要么全为0，可以将数组先排序，到固定位为正数时，迭代便可停止。

 

 

 

class Solution(object):

    def threeSum(self, nums):
        nums.sort()
        result = []
        for start in range(len(nums)):

            if start > 0 and nums[start] == nums[start-1]:　　　　# 跳过重复的固定位
                continue

            i = start+1
            j = len(nums)-1
            oneSum = -nums[start]

            while i < j and nums[start] <= 0:
                twoSum = nums[i] + nums[j]
                if twoSum > oneSum:
                    j -= 1
                elif twoSum < oneSum:
                    i += 1
                else:
                    temp = [nums[start], nums[i], nums[j]]
                    result.append(temp)
                    while i < j and nums[i] == nums[i+1]:　　　　# 跳过重复的，已判断的i
                        i += 1
                    while i < j and nums[j] == nums[j-1]:       # 跳过重复的，已判断的j
                        j -= 1
                    i += 1
                    j -= 1
        return result