吴恩达机器学习笔记3-应对模型误差

一、术语

1、欠拟合与过拟合：

　　欠拟合：模型预测数据与实际数据相差太大（图1-1左边）；

　　过拟合：模型预测结果对于现有实的际数据有很好的准确度，但模型不能推广应用到其它新数据（图1-1右边）；

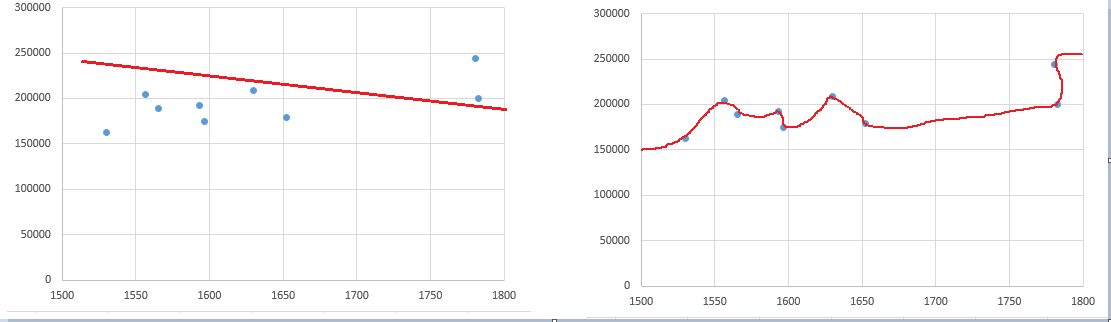
　　　　　　　　　　　　　　　　　　　　　　　　　　　【图1-1】

2、训练集、验证集、测试集：

　　训练集：训练数据，用以梯度下降，使得误差最小化；

　　验证集：测试当前模型的准确率，我们由此调节迭代次数、学习率...；

　　测试集：用以最后测试准确率的数据集；

 

3、正则化：

　　限制目标函数，以免过拟合；

 

4、偏差、方差

　　偏差：预测结果与实际的误差；

　　方差：模型对不同批的同类型数据（例如 训练集、验证集），输出结果的波动程度；

 

二、应对方法与问题纵览

1、获取更多训练数据——高方差（过拟合）；

2、减少特征值——高方差（过拟合）；

3、增加特征值——高偏差（欠拟合）；

4、缩小正则化项中的λ——高偏差（欠拟合）；

5、增大正则化项中的λ——高方差（过拟合）；

 

三、线性回归代价函数正则化公式

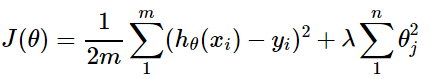
其中，J(θ)为代价函数，x,y为训练数据，θ为模型参数，式子末尾的正则化项是用来缩小每一个参数的。

 过拟合出现的原因是模型函数过于复杂，当加上一个正则化项后，可以很好地控制参数的大小，简化模型。

当λ越大，会使得参数越小，则模型函数会更加简化，从而模型易于推广、泛化。

 

四、逻辑回归代价函数正则化公式

 

五、诊断方差、偏差

　　记 训练集产生的代价（误差）—— J(θ)_train，验证集产生的代价（误差）—— J(θ)_cv

　　总体方法是把 J(θ)_train与 J(θ)_cv比较：若J(θ)_train与J(θ)_cv都大，说明模型函数欠拟合，产生高偏差，预测得不够准确；

若J(θ)_train远远小于J(θ)_cv说明模型函数过拟合，产生高方差，模型函数推广泛化性差。如图5-1

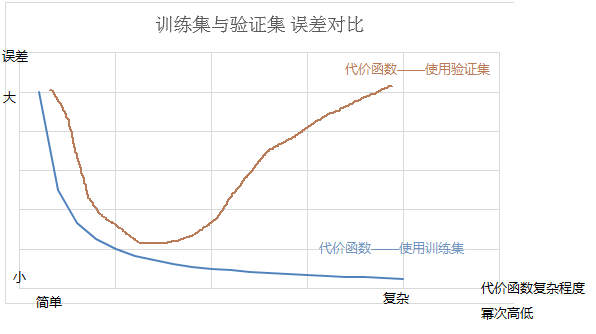
　　　　　　　　　　　　　　【图5-1】