吴恩达机器学习笔记2-单变量逻辑回归

一、逻辑回归（Logistics 回归）直观印象

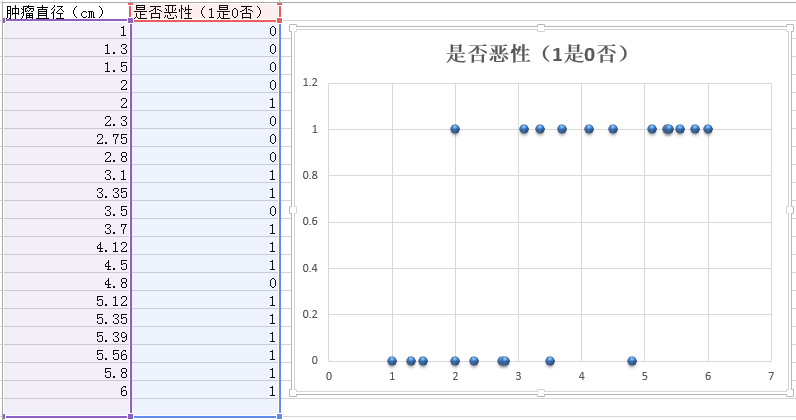
逻辑回归是用来解决分类问题，比如给定一个肿瘤的直径大小（x），要预测出它是良性（0）还是恶性（1），如图1-1。

　　　　　　　　　　　　　　　　　　　　　　　　【图1-1】

如图中我们可以直观地看到，当尺寸大于3cm，是恶性肿瘤的概率就比较大，当尺寸大于5cm，几乎百分之百是恶性的。

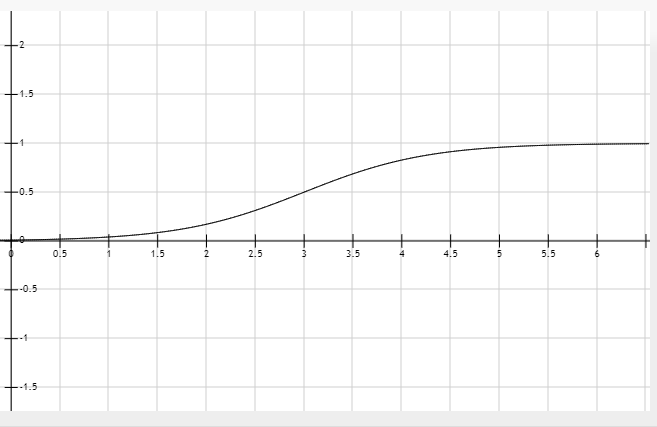
于是图中的关系就可以转换成概率与尺寸的函数图像，如图1-2所示。

　　　　　　　　　　　　　　　　　　【图1-2】

图中纵轴表示1、0的概率，横轴表示尺寸，如尺寸大小为3cm时，良性或恶性的概率各50%。随后尺寸越大，恶性的可能则越大，反之亦然。

进一步地将该图像一般化，将尺寸大小放缩之后（如x-3），当尺寸小于0时偏向良性，尺寸大于0时，偏向恶性。即可得如下被图像（称为sigmoid函数图像）。

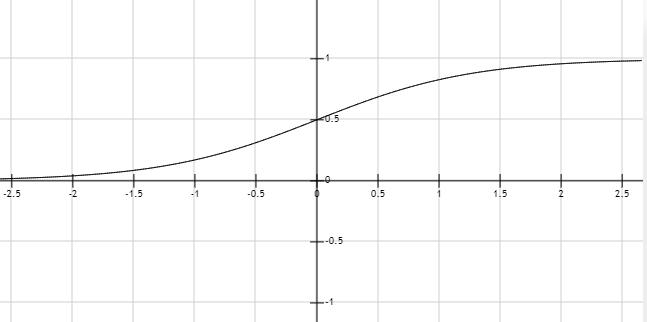
　　　　　　　　　　　　　　　　　　　　【图1-3】

 

二、如何分类

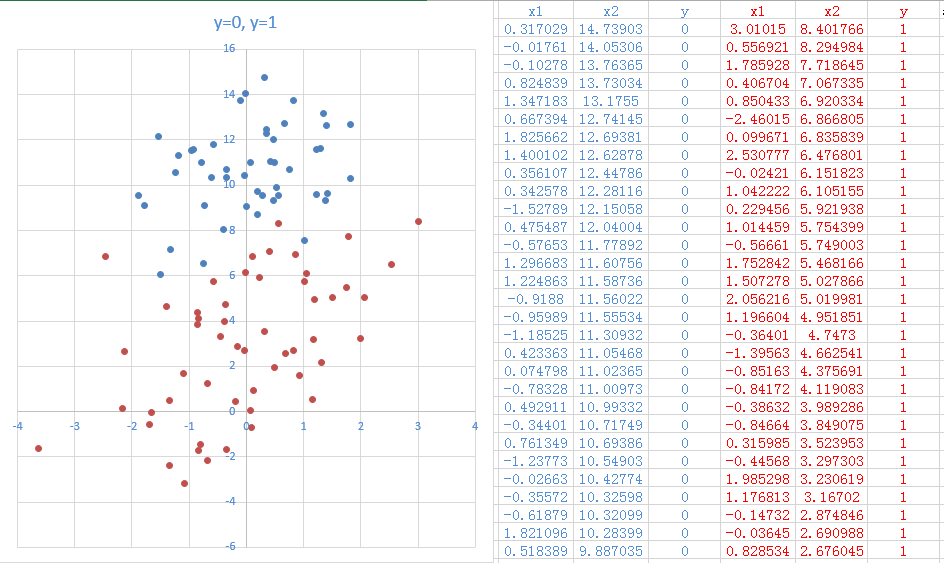
通过给定且已经分好类的数据集，我们如何来建立模型呢？如图2-1（横轴为x1，纵轴为x2，蓝色点为0，红点为1）.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　【图2-1】

从图中我们可以直观地看到红点分布在图偏下方，蓝点分布在图偏上方。

 

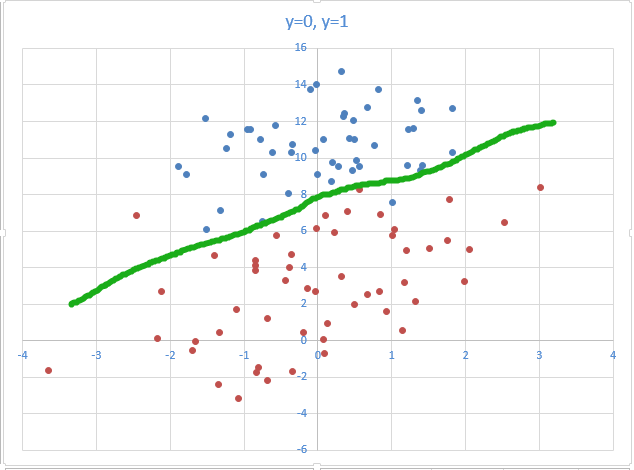
　　　　　　　　　　　　　　　　　　　　【图2-2】

图中绿色的线大致上把红蓝点的分布区域一分为二，该线可称之为决策界限（决策边界），绿线往上为1，绿线往下为0，逻辑回归主要目的就是求出这么‘一条线’。

在上文我们说到，可以将分类数据建立一个sigmoid函数，其表达式为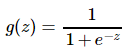：，当g(z)>0.5（即z>0）时，趋向1；当g(z)<0.5（即z<0）时，趋向0。

因此，定义我们的逻辑回归的预测函数为h(W^Tx) = g(W^Tx)，其中W^Tx是w₁*x₁+w₂*x₂+...+w_n*x_n。即可推得：W^Tx=0时是决策边界(绿线)；当W^Tx>0时，趋向1；W^Tx<0时，趋向0。

其中图2-2的预测函数h(W^Tx)可以表示为。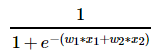

 

三、代价函数

关于预测函数h(W^Tx)，我们当然希望它误差越小越好。

于是便建立相关的代价函数J(W^T)，以求出其最小代价（误差）。

在代价函数J(W^T)中，通过给定x1,x2的值预测出来的结果与实际结果误差越大，则代价越大，反之亦然。

于是便有了如此的一个代价函数（具体推导过程请自行参阅相关资料）：

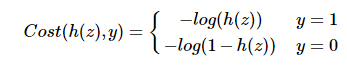
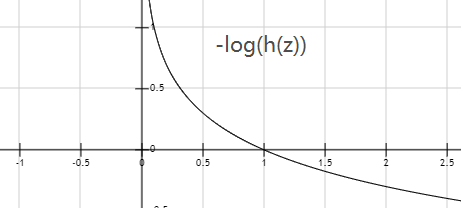
　　　　　　　　　　　　　【图3-1】

　　　　　　　　　　　　 【图3-2】

 图3-1为y=1的代价函数图像，其中纵轴为代价，横轴为预测值。可以看到预测值=1时代价最小，为0，若预测值越不精准，其代价就会越大。图3-2同理。

为了便于计算，将函数合并为一个式子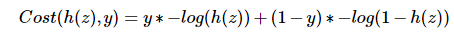： 　　　　　　（当y=1时，式子右边后半便为0，只计算前半部分）。

于是代价函数为

 

四、梯度下降

其求最小代价与线性回归一致，这里直接给出计算公式。

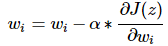
α为学习率，重复以上过程直至收敛。

最终得到W^T的各个值，代入h(W^Tx)便为我们所求的逻辑回归预测函数。