吴恩达机器学习笔记1-单变量线性回归

一、关于回归方程的直观印象

　　我们有一批关于'房屋面积'和'房子价格'的数据，如图1-1：

　　　　　　　　　　　　　　　　【图 1-1】

　　从图右边中可以很直观地看出，大致上，随着房屋面积的增加，房屋的售价也在提高，也就是它俩之间有'某种关系'。

　　而后，我们想，要是我有一套房子，面积是x平方，那应该标价多少钱才合适呢？

　　于是我们就在现有的数据中，找出面积与售价之间的关系，该关系以数学语言表达就是一条线性回归方程（h(x)=kx+b，y为价格，x为面积），面积为自变量，售价为因变量。

　　最后将我们手上这套房子的面积代入到方程中，就可以计算出应该标价多少钱。

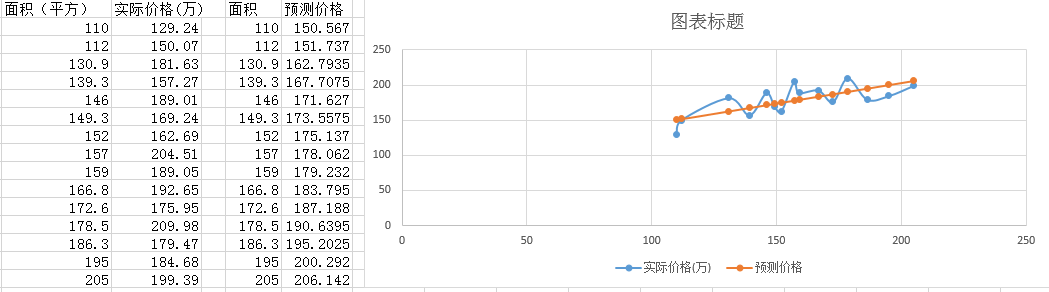
　　　　　　　　　　　　　　　　【图 1-2】

　　如图1-2右边橙色的线，便是我们通过计算得出的回归方程所绘制的线，再回代房子面积所得出的预测价格，它很'直'。

　　尽管线性回归方程不是百分之百符合现实数据，但是它使得一些看起来杂乱的数据更加可量化、计算以及利用，回归方程是一种'折中'。

 

二、方程误差

　　由图1-2右边可以看出，我们的预测价格与实际价格是有误差的，每处的误差为（预测价格-实际价格），所有误差加起来便是总误差，求总误差的方程便称为代价函数（或 损失函数、成本函数、loss function），以J(k,b)表示。

　　其中每处的误差为（预测价格-实际价格），用符号表示便是 h(x_i) - y_i  （h(x)为回归方程所计算的预测价格，x_i，y_i表示第i个数据）；

　　总误差便为∑（h(x_i) - y_i），但这样做有一个问题，误差有负有正，它们会相互抵消，因此我们为每处误差加上平方，即 ∑（h(x_i) - y_i）²，其中为了方便后续计算，我们将其写成J(k,b)=1/2m·∑（h(x_i) - y_i）²

　　当我们想用回归方程去预测房子价格时，当然希望误差最小，即求出代价函数的最小值。

 

三、最小误差

　　在数学中如何计算最小值？

　　答：求导->求驻点、断点、不可导点->通过比较

　　但是实际生活的数据中往往很复杂，可能找到驻点很困难、可能数据量大或没有边界（端点）......所以我们只能采取近似的方法去求的最小值。

　　求最小值的方法是，选择一个起点，一步一步地去探索最小值，最终收敛。

　　在代价函数J(k,b)中，x_i ，y_i  都是已知数据，唯有h(x)中的k，b未知，求最小值实质就是求'合适'的k，b，使得该代价函数最小。

　　求'合适'的k，b的公式，k₀₌₀,b₀₌₀为初始值：

　　　　

　　其中：a为学习率，即每次要迈多大的步子去探索，a值太大（容易扯着蛋）容易‘跨’过最小值；太小，则探索时间长。

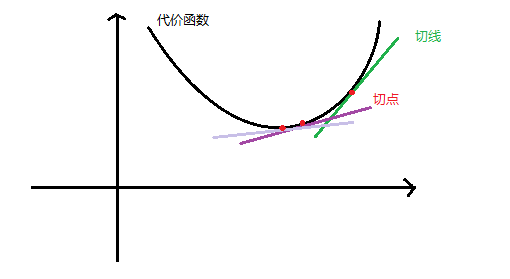
　　为什么要对k，b分别求偏导呢？我们以二维的图像来阐明。设代价函数为J(θ)

　　　　　　　　　　　　【图3-1】

　　图3-1中，图中红色切点便是初始值，求导所得的便是切线的斜率，由图可见该绿色切线斜率为正数。

　　于是 θ = θ - a*一个正数，此时θ变小了点，红点往下移，更加靠近图像最低点（代价函数最小值）；

　　不断重复该过程，切线将趋于平缓，斜率趋于0，函数最小值便收敛了，此过程称之为梯度下降。

　　　　　　　　　　　　【图3-2】

 

四、补充，关于导数的本质

　　导数是什么？

　　导数是变化率，导数是切线斜率，导数是速度........

　　以一元函数而言，导数其实是： 当x变化一点点，y会变化了多少，这个“多少”便是导数。