START:
2021-08-08
08:39:54
问题一:01背包问题
相关问题链接:
https://www.acwing.com/problem/content/2/
问题详情:
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数N,V用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
这就是背包问题,我们先用最朴素的方法,针对每个物品是否放入背包进行搜索。具体实现如下:
//输入
int n,W;
int w[MAX_N],v[MAX_N];
//从第i个物品开始挑选总重小于j的部分
int rec(int i,int j)
{
int res;
if(i==n)//已经没有剩余物品了
res=0;
else if(j<w[i])//无法挑选这个物品
res=rec(i+1,j);
else //挑选和不挑选的两种情况都尝试一下
res=max(rec(i+1,j),rec(i+1,j-w[i]+v[i]) ;
return res;
}
void solve(){
printf("%d\n",rec(0,W));
}
只不过这种方法的搜索深度是n,而且每一层的搜索都需要两次分支,时间复杂度是O(2n),当n比较大时就超时了,为了优化算法,我们找出函数递归调用的路径:
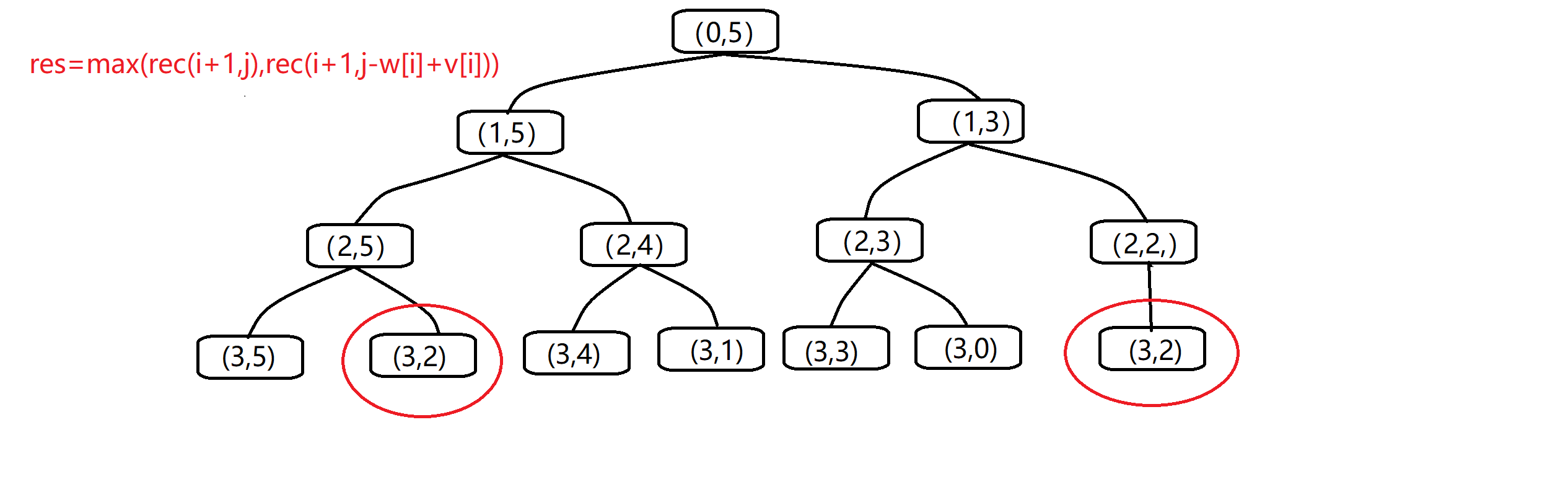
我们可以看到,在调用函数rec(0,5)的时候,在第三层调用中调用了两次rec(3,2),所以除第一次调用参数相同的函数,其他调用都是重复了,白白浪费了计算时间,所以使用记忆化搜索。
int dp[MAX_N+1][MAX_W+1];//记忆化数组
int rec(int i,int j)
{
if(dp[i][j]>0)return dp[i][j];
int res;
if(i==n){
res=0;
}else if(j<w[i])res=rec(i+1,j);
else res=max(rec(i+1,j),rec(i+1,j-w[i]+v[i]));
//将结果记录在数组中0
return dp[i][j]=res;
}
void solve(){
memset(dp,-1,sizeof dp);
printf("%d\n",rec(0,W));
}
对于同样的参数,只会在第一次被调用的时候会执行递归部分,第二次之后都会直接返回。参数的组合不超过nW种,所以时间复杂度是O(nW)。
接下来我们来研究一下前面算法用到的记忆化数组,定义dp[i][j]:从第i个物品开始挑选总重小于j时,总价值的最大值。所以我们有:

怎么推导的呢,我们看:
如果下一个物品的体积大于j,那么下一个物品一定不能加入背包,所以dp[i][j]=dp[i-1][j] (j<w[i])
如果下一个物品的体积小于j,那么可以加入,我们取dp[i-1][j]和dp[i-1][j-w[i]]+v[i]的最大值就行
所以01背包问题核心代码就是这个,具体实现:
void solve(){
for(int i=1;i<=N;i++)
{
for(int j=0;j<=V;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=v[i])dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
}
}
cout<<dp[N][V]<<endl;
}
这是二维的01背包,也可以压缩成一维数组做,我们看核心代码:dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i])
我们可以看出所有的第i层的dp都是用第i-1层来计算的。
所以我们将一维坐标全部删掉得到
void solve(){
for(int i=1;i<=N;i++)
{
for(int j=0;j<=V;j++)
{
dp[j]=dp[j];
if(j>=v[i])dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[V]<<endl;
}
但是上述标红的地方,我们先化简一下:
void solve(){
for(int i=1;i<=N;i++)
{
for(int j=V;j>=v[i];j--)
{
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[V]<<endl;
}
关于这个标红的地方,我们很明显得看出,j的顺序变了,如果不变的话,核心代码(dp[j]=max(dp[j],dp[j-v[i]]+w[i])中的最后一个式子:dp[j-v[i]]+w[i],如果我们从小到大遍历j的话,因为j-v[i]一定小于j,所以dp[j-v[i]]在更新dp[j]之前就被更新了,但是我们更新dp[j]需要的是上一层的数据,但是dp[j-v[i]]已经是更新为第i层的了,所以我们从大到小遍历,那么更新dp[j]的时候dp[j-v[i]]还没有被更新。
问题二:完全背包问题
相关题目链接:
https://www.acwing.com/problem/content/3/
题目详情:
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数 N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
10分析:
完全背包问题不同于01背包问题,在完全背包问题中,同一件物品可以选择多件,我们试着写出递推关系:
令dp[i][j]:从前i种物品中挑选总量不超过j时总价值的最大值。那么递推关系为:
dp[0][j]=0
dp[i][j]=max{dp[i-1][j-k*w[i]]+k*v[i] | 0<=k}
我们尝试编写这个递推关系求解的程序:
int dp[MAX_N+1][MAX_W+1];
void solve(){
for(int i=1;i<=n;i++)
for(int j=0;j<=w;j++)
for(int k=0;k*w[i]<=j;k++)
dp[i][j]=max(dp[i][j],dp[i-1][j-k*w[i]]+k*v[i]);
}
这样的程序形成了三层循环,时间复杂度为O(nW2),这样并不够好。
我们这样看,我们最后求得的dp[i][j]是dp[i-1][j]和dp[i-1][j-k*w[i]]+k*v[i]求最大值,我们来看dp[i][j]:
dp[i][j]=max{ dp[i-1][j-k*w[i]]+k*v[i] | 0<=k }
==>max(dp[i-1][j],max{dp[i-1][j-k*w[i]]+k*v[i] |1<=k} )
==>max(dp[i-1][j],max{dp[i-1][(j-w[i])-k*w[i]+ k*v[i] | 0<=k }+v[i] )
==>max(dp[i][j],dp[i][j-w[i]]+v[i])
所以我们可以优化第三个for循环,不需要关于k的循环辣!
具体实现:
void solve(){
for(int i=1;i<=n;i++)
for(int j=0;j<=W;j++){
dp[i][j]=dp[i-1][j];
if(j>=w[i])dp[i][j]=max( dp[i][j],dp[i][j-w[i]]+v[i] );
}
printf("%d\n",dp[n][W]);
}
问题三:多重背包问题I
相关题目链接:
https://www.acwing.com/problem/content/4/
题目详情:
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数 N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<vi,wi,si≤100
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
多重背包问题相对于01背包和完全背包,它能选取的物品的数量是有限的,储存在数组s[N]中,
其实多重背包问题的思路和完全背包是完全一样的,就是最后一个判断条件改动一下:
void solve(){
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
for(int k=0;k<=s[i]&&k*v[i]<=j;k++)
dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]*k]+w[i]*k);
}
}
cout<<dp[n][m]<<endl;
}
问题四:多重背包问题II
相关问题链接:
https://www.acwing.com/problem/content/5/
题目详情:
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数 N,V 用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si 用空格隔开,分别表示第 ii 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤1000
0<V≤2000
0<vi,wi,si≤2000
提示:
本题考查多重背包的二进制优化方法。
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
多重背包问题II是问题I的升级版,就是加强了数据,使得原来的三层循环时间复杂度太高,需要进行优化。
怎么优化nie~
我们可以将所有的背包打包成新的背包,使得任取几个新背包都能取到原来背包都能取得的范围,然后使用01背包求解。
比如我们有4种物品,每种物品都有500个,那么我们将每种物品分别打包,例如第一种物品的新背包:
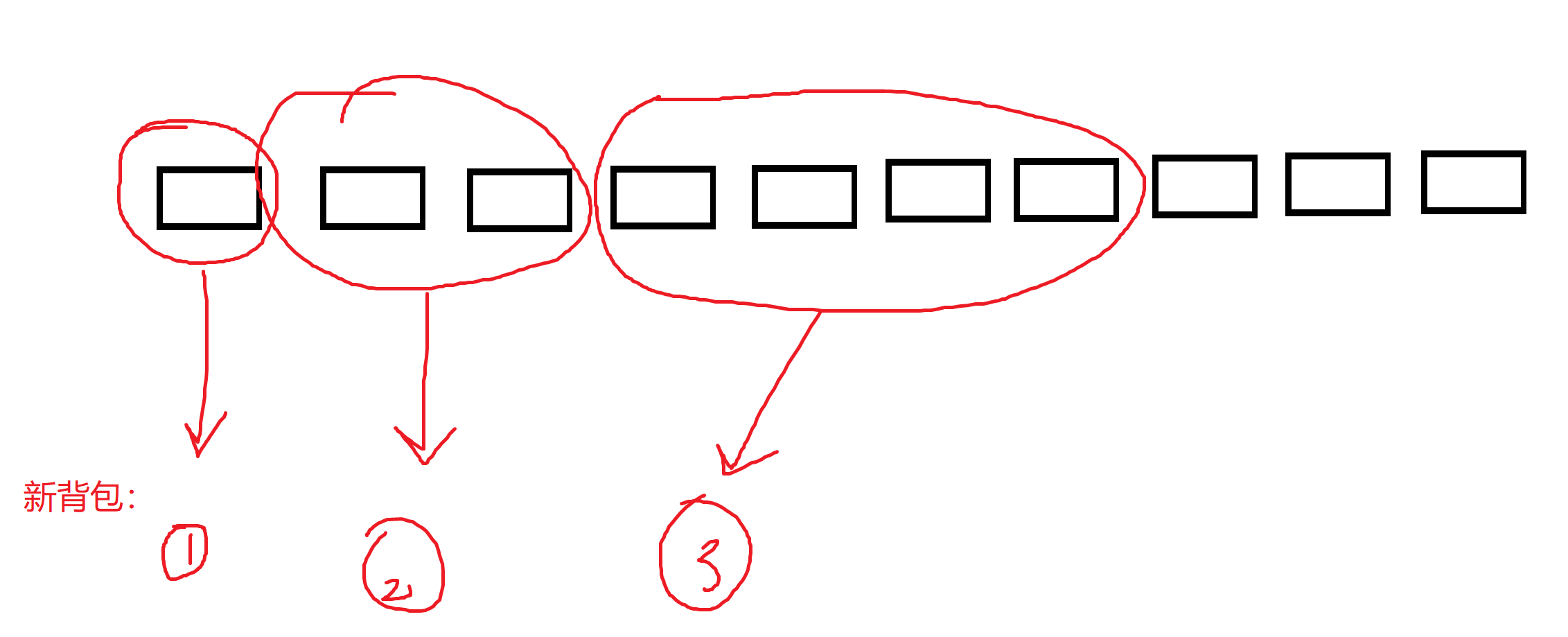
如图,我们将500个背包分别打包1个,2个,4个,8个,16个,32个,64个,128个(!到这时,还剩下245个背包),245个。
我们如果需要100个第一种的物品,就拿分别装着64个,32个,4个物品的新背包,这样就将原来拿取背包的O(N)的时间复杂度变成了logN。
当然,我们需要一个新的背包的编号,就用cnt来计数,分别满1,2,4,8,16.......以及不满2k 的剩下的背包数。
所以我们在读入数据的同时更新新背包的信息。
#include<iostream>
using namespace std;
const int N=25000;
int v[N],w[N],s[N];
int dp[N];
int main()
{
int n,m;
cin>>n>>m;
int cnt=0;
for(int i=1;i<=n;i++){
int a,b,s;
cin>>a>>b>>s;
int k=1;
while(k<=s){
cnt++;
v[cnt]=a*k;
w[cnt]=b*k;
s-=k;
k=k*2;
}
if(s>0){
cnt++;
v[cnt]=a*s;
w[cnt]=b*s;
}
}
return 0;
}
最后我们使用01背包的结构解题:
#include<iostream>
using namespace std;
const int N=25000;
int v[N],w[N],s[N];
int dp[N];
int main()
{
int n,m;
cin>>n>>m;
int cnt=0;
for(int i=1;i<=n;i++){
int a,b,s;
cin>>a>>b>>s;
int k=1;
while(k<=s){
cnt++;
v[cnt]=a*k;
w[cnt]=b*k;
s-=k;
k=k*2;
}
if(s>0){
cnt++;
v[cnt]=a*s;
w[cnt]=b*s;
}
}
n=cnt;
for(int i=1;i<=n;i++){
for(int j=m;j>=v[i];j--){
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
cout<<dp[m]<<endl;
return 0;
}
问题五:分组背包问题:
相关问题链接:
https://www.acwing.com/problem/content/9/
问题详情:
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i 是组号,j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,V 用空格隔开,分别表示物品组数和背包容量。
接下来有 N 组数据:
- 每组数据第一行有一个整数 Si,表示第 i 个物品组的物品数量;
- 每组数据接下来有 Si 行,每行有两个整数 vij,wij,用空格隔开,分别表示第 i 个物品组的第 j 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<Si≤100
0<vij,wij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例:
8
分析:
分组背包问题要考虑的是每一组选哪一个物品的问题,数据较小所以可以枚举。
void solve(){
for(int i=1;i<=n;i++){
for(int j=m;j>=0;j--){
for(int k=0;k<s[i];k++){
if(v[i][k]<=j)dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k]);
}
}
}
cout<<dp[m]<<endl;
}
再加上处理输入的基本架构,完整代码:
#include<iostream>
using namespace std;
const int N=110;
int s[N],v[N][N],w[N][N];
int dp[N];
int n,m;
void solve(){
for(int i=1;i<=n;i++){
for(int j=m;j>=0;j--){
for(int k=0;k<s[i];k++){
if(v[i][k]<=j)dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k]);
}
}
}
cout<<dp[m]<<endl;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>s[i];
for(int j=0;j<s[i];j++)
cin>>v[i][j]>>w[i][j];
}
solve();
return 0;
}
END:
2021-08-08
16:04:12



