【机器学习】机器学习入门04 - 线性回归

在前面的3篇文章中，我们借助kNN算法介绍了机器学习中的分类问题。

总的来说，分类(classification)和回归(regression)是机器学习中的两大类问题。它们其实都是在做同一件事情——将输入转化为输出。区别在于，分类得到的输出是离散值，例如之前的癌症问题中的良性（0）和恶性（1）；而回归的得到的输出是连续值。

本篇文章，将开始讨论回归问题。我们从最简单的线性回归开始。

1. 线性回归的概念

所谓线性回归，就是用自变量的线性函数来给出任意给定自变量下的预测值。它非常简单，并且在特定问题背景下可以起到很好的回归效果。

我们先来试着考虑一元的线性回归（也称为简单线性回归）。

我们知道，一般的一元线性函数的表达式是：

   

 

 

而对于机器学习，数据自然不可能完全属于一条直线。在这样的前提下，假如数据的分布近似于线性，我们是否可以用这样一条直线来进行拟合，从而进行预测呢？答案当然是肯定的，于是我们需要考虑的是，如何确定这条用于拟合的直线。

事实上，很容易想到，给定一组近似线性的数据点，我们有无数条直线可以逼近这些点。那么，我们该如何对它们进行评估，并且选出我们认为最合适的一条呢？

直观地说，我们希望数据点尽可能均匀地分布在直线两侧。更深一步来分析，这么做的目的，是为了尽可能减小数据点与直线之间的距离。因为距离越大，意味着误差可能越大。所以，我们考虑利用所有数据点与直线之间的距离来衡量回归直线的优劣。

 

 

 

2. 最小二乘法

2.1 损失与风险

第1部分中，我们构造了一个函数  。我们把这个函数称为上述线性回归的平方损失函数。

什么叫损失函数？

损失函数描述了单个样本预测值和真实值之间误差的程度。用来度量模型一次预测的好坏。

常用的四种损失函数：

1. 0-1损失函数（用于分类问题，分类正确取0，分类错误取1）
2. 平方损失函数（即所有预测值与真实值之差的平方和）
3. 绝对损失函数（即所有预测值与真实值之差的绝对值之和）
4. 对数损失函数（利用了极大似然估计思想，具体见https://www.cnblogs.com/klchang/p/9217551.html）

损失函数通常记作，针对的是单个数据点。那么，由局部到整体，就引出了风险函数的概念。

风险函数又称为期望风险，是指损失函数的期望。

在特定的训练数据集之下，我们不知道数据集的分布，没有办法计算期望，我们能计算的只有平均值。我们将这个平均值称为经验风险。

经验风险最小的模型，称为最优模型。

概率论与数理统计告诉我们，可以用样本均值来近似估计分布期望。然而，样本容量不大时，有可能出现过拟合的状况。因此，我们在经验风险后加上一个正则化项（罚项），称之为结构风险。用结构风险代替经验风险，可以很好地避免过拟合的问题。

接下来，就可以正式介绍最小二乘法了。

2.2 最小二乘法

所谓最小二乘法，就是一种求 的最小值的方法。（二乘即平方之意）

 

 

在线性回归中，我们希望通过最小二乘法求出使得上式最小时的a和b的值。

对a和b求偏导数，偏导函数的零点即为上式的极值点，也就是我们需要的a和b的最优值的可能值。最终结果如下：

 

 

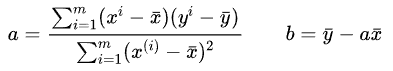
 具体推导过程较为复杂，这里不再展开，可参考https://www.cnblogs.com/code-juggler/p/8406449.html

 

3. 代码实现

第二部分中，我们已经利用最小二乘法推导出了简单线性回归系数的最优值的公式。这样一来，我们的代码实现就非常简单了。

x_mean = np.mean(x)
y_mean = np.mean(y)

num = 0.0
d = 0.0
for x_i,y_i in zip(x,y):  
    num = num + (x_i - x_mean) * (y_i - y_mean)
    d = d + (x_i - x_mean) ** 2
a = num / d
b = y_mean - a * x_mean

我们利用一个循环，计算出了a和b的值。这样，对于任意符合要求的x值，我们都可以利用y=ax+b对y值进行回归预测了。

然而，我们上面所做的运算，实际上可以表达成两个向量的数量积。用数量积进行运算，可以大大缩短运算时间。因此，我们可以构造向量，然后利用numPy库中的dot函数优化我们的运算过程。

虽然在我们看来，直接循环相加和利用向量的数量积计算似乎是完全相同的运算过程，但事实上，数量积运算并不是我们想象的这样循环相加，而是利用了矩阵的特性优化运算。因此，效率会远高于我们直接构造的for循环（特别是当数据集特别大时）。

 

4. 多元线性回归

上面讲的是每个数据点只有一个输入变量的线性回归，也就是一元线性回归。

事实上，当有多个变量输入（比如癌症的发现时间、癌症的大小）时，我们同样可以进行线性回归。这就是多元线性回归。

为了形式简洁，我们直接使用矩阵记号来表示数据集。用矩阵X_b表示数据集的输入，每个行向量表示一个数据点的各指标，每个列向量表示所有数据点的某一指标值。用向量 θ=(θ₁, θ₂, θ₃, ..., θ_n) 表示我们所需要的线性回归函数的系数。我们构造线性回归函数 y=θ·X 的过程就是其实就是找到使风险函数 |(Y-θ·X_b)^T·(θ·X_b)| 最小的向量θ。

结果如下：

 

我们没有必要了解其推导过程。直接使用这一结果，就可以得到我们需要的回归方程。