猪猪的机器学习笔记(七)最大熵模型
最大熵模型
作者:樱花猪
摘要:
本文为七月算法(julyedu.com)12月机器学习第七次课在线笔记。熵,这个概念对于我们来说既熟悉又陌生,熟悉的是我们在许多领域都会碰到熵这个概念,陌生的是如果真的让你解释它又说不清道不明。本次课程讨论了熵的概念并详细解释了最大熵模型。这次课承上启下,将前几次课程所埋的坑一一填起,又为接下来更加深入的机器学习做了铺垫。
引言:
熵的概念对我来说既陌生又熟悉,在看论文中常常会碰到“熵”但是却总是觉得差一口气来解释它。通过这次课程,终于对于熵这个概念有了一个更加具体和感性的认识,不再单单局限于冰冷的公式。最大熵模型在机器学习以及其他算法中都有所提到,是一种非常常见又有用的方法。本文首先阐述了有关于“熵”的一些概念,然后详细的介绍了最大熵模型和其应用。
预备知识:
参数估计、概率论、方阵的导数
最大熵模型
ICA
一、熵及相关概念
1、信息量
当一个小概率事件发生了,那么这个事件的信息量很大;反之如果一个大概率事件发生了,这个事件的信息量就很少。根据这个描述,我们可以构造一个信息量的表达式:
若事件A发生的概率为P,那么A的信息量为:![]()
2、熵
对随机事件的信息量求期望,得熵的定义:
![]()
注:经典熵的定义,底数是2,单位是bit
3、联合熵Joint Entropy
![]()
4、条件熵
在Y发生的前提下,X发生“新”带来的熵 。
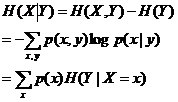
互信息表示法:
![]()
5、相对熵
相对熵,又称互熵,交叉熵,鉴别信息,Kullback 熵,Kullback-Leible(KL)散度等。
相对熵可以度量两个随机变量的“距离”,K-L距离;是非常重要的概念。:K-L距离是非对称的。
公式:、
设p(x)、q(x)是X中取值的两个概率分布,则p对q的相对熵是
![]()
假定使用KL(Q||P),为了让距离最小,则要求在P为 0的地方,Q尽量为0。会得到比较“窄”的分布曲 线;
假定使用KL(P||Q),为了让距离最小,则要求在P不为0的地方,Q也尽量不为0。会得到比较“宽”的分 布曲线;
6、互信息
两个随机变量X,Y的互信息,定义为X,Y 的联合分布和独立分布乘积的相对熵。
![]()
![]()
注:可以联系“互信息”
7、整理

![]()
对偶式:
![]()
![]()
![]()
![]()
二、最大熵模型
1、最大熵模型原则
a. 承认已知事物(知识)
b. 对未知事物不做任何假设,没有任何偏见
2、最大熵模型Maxent
![]()
P={p | p是X上满足条件的概率分布}
3、求解过程:
最大熵模型MaxEnt的目标拉格朗日函数L

归一化因子:

5、应用:
ICA独立成分分析
ICA的目标函数:
ICA可以用最大化各个成分的统计独立性作为目标函数。
“独立性”判断原则为:
a. 最小化各个成分的互信息(MMI、K-L散度、最大熵)
b. 最大化各个成分的非高斯性
PCA:主成分分析;分出来是不相关的。
ICA:独立成分分析。分出来是独立的。
6、极大似然估计和最大熵模型
根据极大似然估计的正确性可以断定:最大熵的解 (无偏的对待不确定性)是最符合样本数据分布的解,即最大熵模型的合理性。
信息熵可以作为概率分布集散程度的度量,使用熵的近似可以推导出基尼系数,在统计问题、决策树 等问题中有重要作用。
熵:不确定度
似然:与知识的吻合程度
最大熵模型:对不确定度的无偏分配
最大似然估计:对知识的无偏理解
知识=不确定度的补集




