Visit my LeetCode

算法复杂度&&数组排序

计算算法的复杂度

目录

  • 时间复杂度
  • 空间复杂度

时间复杂度

  • 什么叫做时间复杂度呢？？

  • 我们来看一个简单的程序

 int n = 10 ;
System.out.println("输出" + n);

这段伪代码运行了多少次呢！ 1次 ，时间时间复杂度为O(1)：常数复杂度/常数阶。

        for (int i = 0 ;i <n; i++){
            System.out.println("第几次"+i);
        }

这个for循环了多少次呢！ n次，时间复杂度为O(n)：线性时间复杂度。

再看下一个

        for (int i = 0 ;i <n; i++){
            for (int j = 0 ;j < n; j ++) {
                System.out.println("第几次" + i+""+j);
            }
        }

这个循环了多少次呢！n*n次，时间复杂度为O(n^2)：平方复杂度。

  • 百度百科对时间复杂度的定义是：在计算机科学中，算法的时间复杂度是一个函数，它定性描述了该算法的运行时间。

我们再把常见的复杂度列举出来看看。

        int j = 0;
        for (int i = 0 ; i < n ; i++) {
            i = i * 2;
            j++;
            System.out.println("第几次"+j);
        }

这个循环了多少次呢！假设我们把次数设为x，那2^x<n，解得次数x=log(n)，时间复杂度为O(log(n))：对数。

        for (int i = 0 ; i < Math.pow(2,n); i++) {
 
            System.out.println("第几次"+i);
        }

这个循环了多少次呢！2n次，时间复杂度为O(2n)：指数复杂度。

  • 举个例子：
    • 快速排序
function quickSort(arr) {
            /* 终止条件 */
            if (arr.length <= 1) {
                return arr;
            }
            /* 找到数组的中间下标 */
            var mid_index = arr.length / 2;
            /* 找到中间值 */
            var mid = arr[mid_index];
            var left_arr = [];
            var right_arr = [];
            for (var i = 0; i < arr.length; i++) {
                // 中点没必要和中点进行比较
                if (i === mid_index) continue;
                if (arr[i] > mid) {
                    right_arr.push(arr[i]);
                } else {
                    left_arr.push(arr[i]);
                }
            }
            return quickSort(left_arr).concat([mid], quickSort(right_arr));

        }
        var arr = [4, 2, 5, 3, 1, 7, 6];
        var res = quickSort(arr)

        console.log(res);

时间复杂度

​ 快速排序涉及到递归调用，所以该算法的时间复杂度还需要从递归算法的复杂度开始说起；

​ 递归算法的时间复杂度公式：T[n] = aT[n/b] + f(n) ；对于递归算法的时间复杂度这里就不展开来说了；

最优情况下时间复杂度

​ 快速排序最优的情况就是每一次取到的元素都刚好平分整个数组(很显然我上面的不是)；

​ 此时的时间复杂度公式则为：T[n] = 2T[n/2] + f(n)；T[n/2]为平分后的子数组的时间复杂度，f[n] 为平分这个数组时所花的时间；

​ 下面来推算下，在最优的情况下快速排序时间复杂度的计算(用迭代法)：

​ T[n] = 2T[n/2] + n ----------------第一次递归

​ 令：n = n/2 = 2 { 2 T[n/4] + (n/2) } + n ----------------第二次递归

​ = 2^2 T[ n/ (2^2) ] + 2n

​ 令：n = n/(2^2) = 2^2 { 2 T[n/ (2^3) ] + n/(2^2)} + 2n ----------------第三次递归

​ = 2^3 T[ n/ (2^3) ] + 3n

​ ......................................................................................

​ 令：n = n/( 2^(m-1) ) = 2^m T[1] + mn ----------------第m次递归(m次后结束)

​ 当最后平分的不能再平分时，也就是说把公式一直往下跌倒，到最后得到T[1]时，说明这个公式已经迭代完了（T[1]是常量了）。

​ 得到：T[n/ (2^m) ] = T[1] ===>> n = 2^m ====>> m = logn；

​ T[n] = 2^m T[1] + mn ；其中m = logn;

​ T[n] = 2^(logn) T[1] + nlogn = n T[1] + nlogn = n + nlogn ；其中n为元素个数

​ 又因为当n >= 2时：nlogn >= n (也就是logn > 1)，所以取后面的 nlogn；

​ 综上所述：快速排序最优的情况下时间复杂度为：O( nlogn )

最差情况下时间复杂度

​ 最差的情况就是每一次取到的元素就是数组中最小/最大的，这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序)

​ 这种情况时间复杂度就好计算了，就是冒泡排序的时间复杂度：T[n] = n * (n-1) = n^2 + n;

​ 综上所述：快速排序最差的情况下时间复杂度为：O( n^2 )

空间复杂度

空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。

简单的讲就是包括下面几部分。

1.存储算法本身所占用的存储空间。

2.算法的输入输出数据所占用的存储空间。

3.算法在运算过程中临时占用的存储空间这三个方面。

int a[] = new int[n];

这个例子的空间复杂度是多少呢？这个数组开辟的空间是多少呢？ O(n)。
总结

时间复杂度和空间复杂度本就是一个相互博弈的过程，一个多另一个就少，根据适当的问题，找到适当的解，这才是好办法。

数组的排序

  • 排序，就是把一个乱序的数组，通过我们的处理，让他变成一个有序的数组
  • 今天我们讲解两种方式来排序一个数组 冒泡排序 和 选择排序

冒泡排序

  • 先遍历数组，让挨着的两个进行比较，如果前一个比后一个大，那么就把两个换个位置

  • 数组遍历一遍以后，那么最后一个数字就是最大的那个了

  • 然后进行第二遍的遍历，还是按照之前的规则，第二大的数字就会跑到倒数第二的位置

  • 以此类推，最后就会按照顺序把数组排好了

    1. 我们先来准备一个乱序的数组

      var arr = [3, 1, 5, 6, 4, 9, 7, 2, 8]
      • 接下来我们就会用代码让数组排序

    2. 先不着急循环，先来看数组里面内容换个位置

      // 假定我现在要让数组中的第 0 项和第 1 项换个位置
// 需要借助第三个变量
var tmp = arr[0]
arr[0] = arr[1]
arr[1] = tmp

    3. 第一次遍历数组，把最大的放到最后面去

      for (var i = 0; i < arr.length; i++) {
  // 判断，如果数组中的当前一个比后一个大，那么两个交换一下位置
  if (arr[i] > arr[i + 1]) {
    var tmp = arr[i]
    arr[i] = arr[i + 1]
    arr[i + 1] = tmp
  }
}

// 遍历完毕以后，数组就会变成 [3, 1, 5, 6, 4, 7, 2, 8, 9]
      • 第一次结束以后，数组中的最后一个，就会是最大的那个数字
      • 然后我们把上面的这段代码执行多次。数组有多少项就执行多少次

    4. 按照数组的长度来遍历多少次

      for (var j = 0; j < arr.length; j++) {
  for (var i = 0; i < arr.length; i++) {
    // 判断，如果数组中的当前一个比后一个大，那么两个交换一下位置
    if (arr[i] > arr[i + 1]) {
      var tmp = arr[i]
      arr[i] = arr[i + 1]
      arr[i + 1] = tmp
    }
  }
}

// 结束以后，数组就排序好了

    5. 给一些优化

      • 想象一个问题，假设数组长度是 9，第八次排完以后

      • 后面八个数字已经按照顺序排列好了，剩下的那个最小的一定是在最前面

      • 那么第九次就已经没有意义了，因为最小的已经在最前面了，不会再有任何换位置出现了

      • 那么我们第九次遍历就不需要了，所以我们可以减少一次

        for (var j = 0; j < arr.length - 1; j++) {
  for (var i = 0; i < arr.length; i++) {
    // 判断，如果数组中的当前一个比后一个大，那么两个交换一下位置
    if (arr[i] > arr[i + 1]) {
      var tmp = arr[i]
      arr[i] = arr[i + 1]
      arr[i + 1] = tmp
    }
  }
}

      • 第二个问题，第一次的时候，已经把最大的数字放在最后面了

      • 那么第二次的时候，其实倒数第二个和最后一个就不用比了

      • 因为我们就是要把倒数第二大的放在倒数第二的位置，即使比较了，也不会换位置

      • 第三次就要倒数第三个数字就不用再和后两个比较了

      • 以此类推，那么其实每次遍历的时候，就遍历当前次数 - 1 次

        for (var j = 0; j < arr.length - 1; j++) {
  for (var i = 0; i < arr.length - 1 - j; i++) {
    // 判断，如果数组中的当前一个比后一个大，那么两个交换一下位置
    if (arr[i] > arr[i + 1]) {
      var tmp = arr[i]
      arr[i] = arr[i + 1]
      arr[i + 1] = tmp
    }
  }
}

    6. 至此，一个冒泡排序就完成了

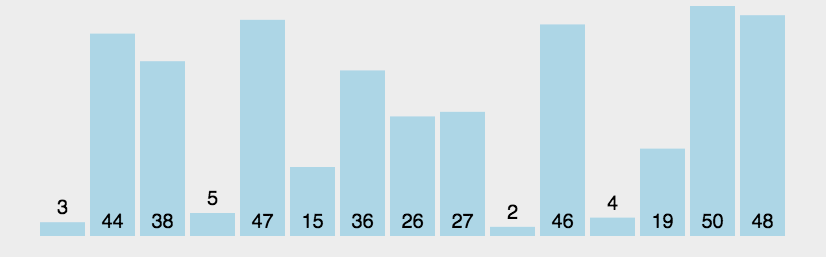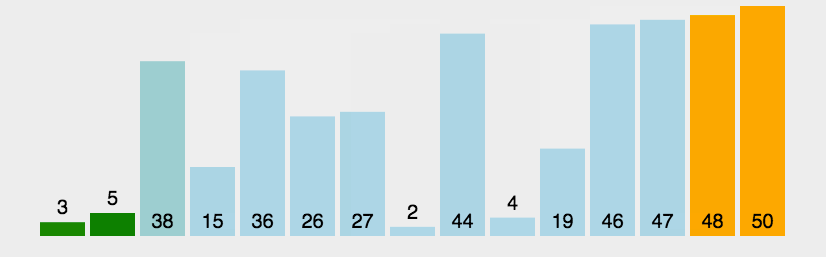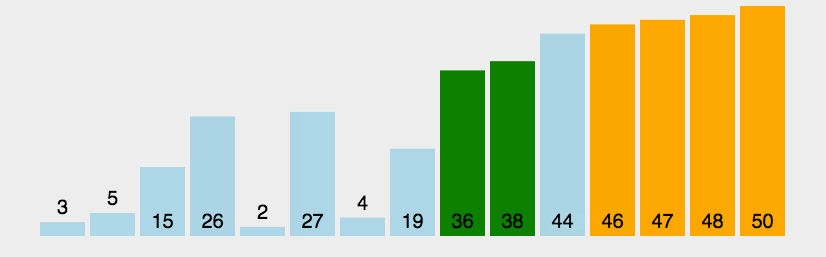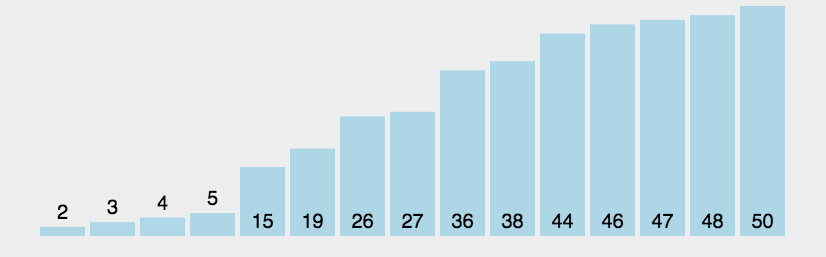
    7. 在这里插入图片描述

选择排序

  • 先假定数组中的第 0 个就是最小的数字的索引

  • 然后遍历数组，只要有一个数字比我小，那么就替换之前记录的索引

  • 知道数组遍历结束后，就能找到最小的那个索引，然后让最小的索引换到第 0 个的位置

  • 再来第二趟遍历，假定第 1 个是最小的数字的索引

  • 在遍历一次数组，找到比我小的那个数字的索引

  • 遍历结束后换个位置

  • 依次类推，也可以把数组排序好

    1. 准备一个数组

      var arr = [3, 1, 5, 6, 4, 9, 7, 2, 8]

    2. 假定数组中的第 0 个是最小数字的索引

      var minIndex = 0

    3. 遍历数组，判断，只要数字比我小，那么就替换掉原先记录的索引

      var minIndex = 0
for (var i = 0; i < arr.length; i++) {
  if (arr[i] < arr[minIndex]) {
    minIndex = i
  }
}

// 遍历结束后找到最小的索引
// 让第 minIndex 个和第 0 个交换
var tmp = arr[minIndex]
arr[minIndex] = arr[0]
arr[0] = tmp

    4. 按照数组的长度重复执行上面的代码

      for (var j = 0; j < arr.length; j++) {
  // 因为第一遍的时候假定第 0 个，第二遍的时候假定第 1 个
  // 所以我们要假定第 j 个就行
  var minIndex = j
  
  // 因为之前已经把最小的放在最前面了，后面的循环就不需要判断前面的了
  // 直接从 j + 1 开始
  for (var i = j + 1; i < arr.length; i++) {
    if (arr[i] < arr[minIndex]) {
      minIndex = i
    }
  }

  // 遍历结束后找到最小的索引
  // 第一堂的时候是和第 0 个交换，第二趟的时候是和第 1 个交换
  // 我们直接和第 j 个交换就行
  var tmp = arr[minIndex]
  arr[minIndex] = arr[j]
  arr[j] = tmp
}

    5. 一些优化

      • 和之前一样，倒数第二次排序完毕以后，就已经排好了，最后一次没有必要了

        for (var j = 0; j < arr.length - 1; j++) {
  var minIndex = j
  
  for (var i = j + 1; i < arr.length; i++) {
    if (arr[i] < arr[minIndex]) {
      minIndex = i
    }
  }

  var tmp = arr[minIndex]
  arr[minIndex] = arr[j]
  arr[j] = tmp
}

      • 在交换变量之前，可以判断一下，如果我们遍历后得到的索引和当前的索引一直

      • 那么就证明当前这个就是目前最小的，那么就没有必要交换

      • 做一我们要判断，最小作引和当前作引不一样的时候，才交换

        for (var j = 0; j < arr.length - 1; j++) {
  var minIndex = j
  
  for (var i = j + 1; i < arr.length; i++) {
    if (arr[i] < arr[minIndex]) {
      minIndex = i
    }
  }

  if (minIndex !== j) {
    var tmp = arr[minIndex]
    arr[minIndex] = arr[j]
    arr[j] = tmp   
  }
}

    6. 至此，选择排序完成

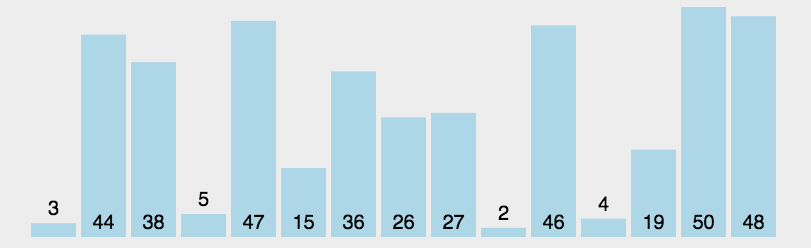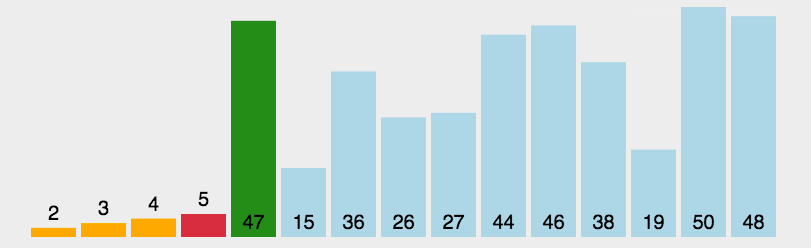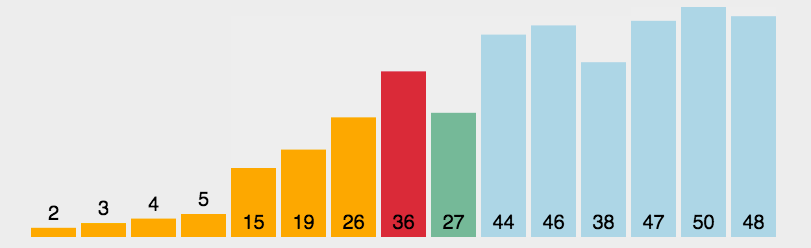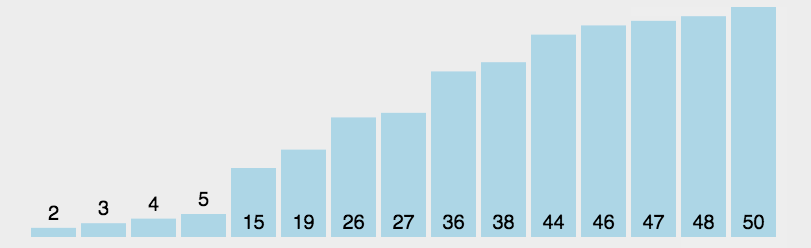
    7. 在这里插入图片描述

快速排序

  • 口诀：找中点，分左右
  • 找中点：找到下标的中位数，分为左右数组。再把左右作为新的数组进行找中点分左右
  • 递归实现
function quickSort(arr) {
            /* 终止条件 */
            if (arr.length <= 1) {
                return arr;
            }
            /* 找到数组的中间下标 */
            var mid_index = arr.length / 2;
            /* 找到中间值 */
            var mid = arr[mid_index];
            var left_arr = [];
            var right_arr = [];
            for (var i = 0; i < arr.length; i++) {
                // 中点没必要和中点进行比较
                if (i === mid_index) continue;
                if (arr[i] > mid) {
                    right_arr.push(arr[i]);
                } else {
                    left_arr.push(arr[i]);
                }
            }
            return quickSort(left_arr).concat([mid], quickSort(right_arr));

        }
        var arr = [4, 2, 5, 3, 1, 7, 6];
        var res = quickSort(arr)

        console.log(res);

img

posted @ 2021-08-03 21:07  Dqarden  阅读(145)  评论(0)    收藏  举报