一致性哈希
在使用分布式缓存时，会用到多台服务器，当我们需要使用某个缓存时，常用的做法是
hash(数据内容) % n
其中，hash() - 对数据内容进行 hash 操作， % - 取模操作，n - 服务器数量。
但如此做，会产生一些问题，例如：
- 在服务器数量发生变化时，缓存的位置会发生变化，需要对所有缓存重新排布，期间会导致大量缓存失效，引起雪崩
一致性哈希 就能很好地解决上述问题
基本结构
一致性哈希 也是使用的取模的方法，不过此时 n 不是当前服务器数量，而是能容纳的服务器最大数量。
下面取 n = 2^32 为例，该值通常也是 2^32，每一个数据内容经过 hash() 后转化为 32 位二进制的 key
把 2^32 中每个值当作一点，其组成一个圆，范围为 0 ~ 2^32-1，称为 hash 环。
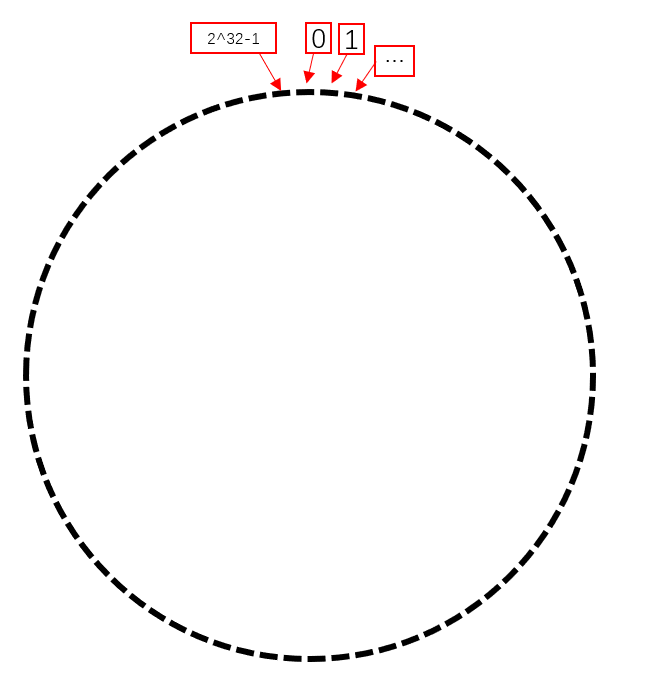
假设目前有服务器 A，B，C。
通过 hash(A_IP) % n ，hash(B_IP) % n，hash(C_IP) % n 后 hash 环上的排布如下
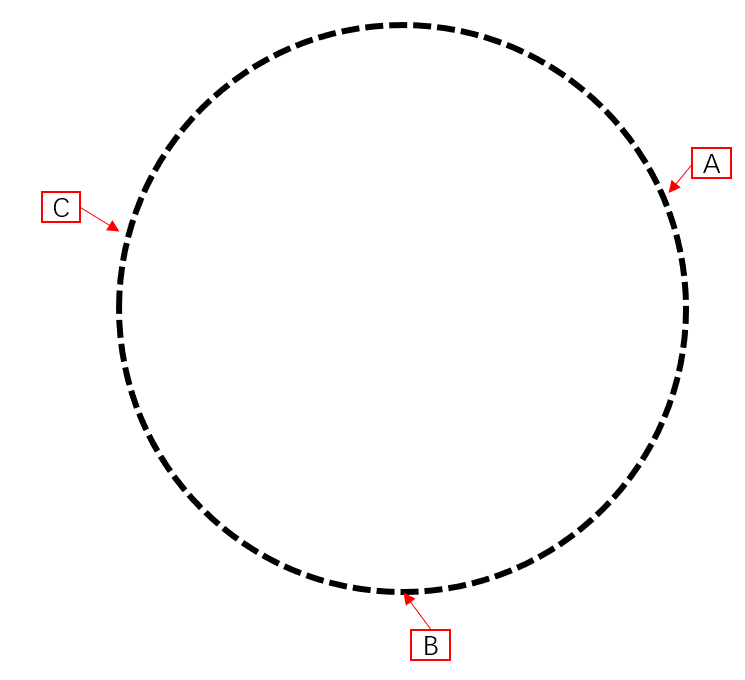
此时，服务器都已经进入 hash 环内，我们进行数据插入，例：
插入数据1内容，hash(D1) % n，插入位置如下
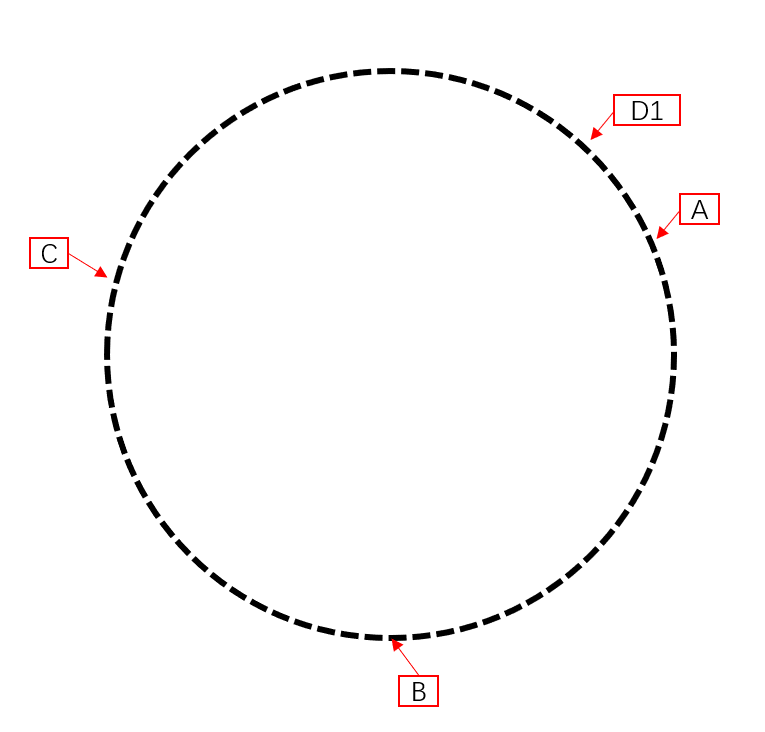
可以看到位置相对服务器有偏移，一致性哈希要求接下来做以下调整：
在数据插入位置顺时针前进，遇到的第一个服务器即使要插入数据的服务器
因此数据1插入后如下，获取数据操作相同，根据 hash 后生成的 key 位置顺时针找到第一个服务器，访问其获得数据
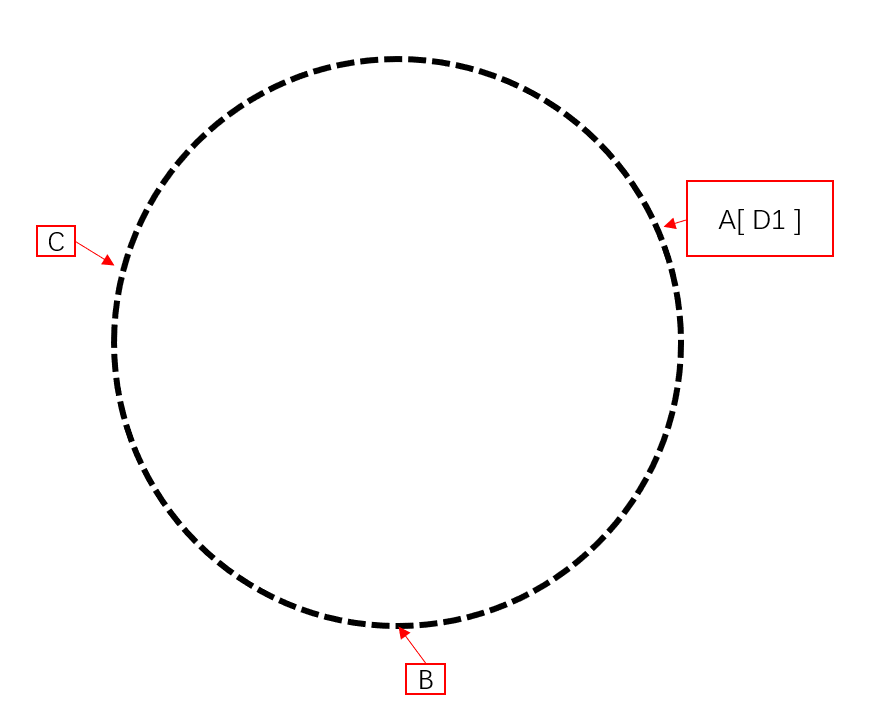
解决修改服务器数量的问题
首先对环初始状态做出假设
假设需要插入的数据位置如下：
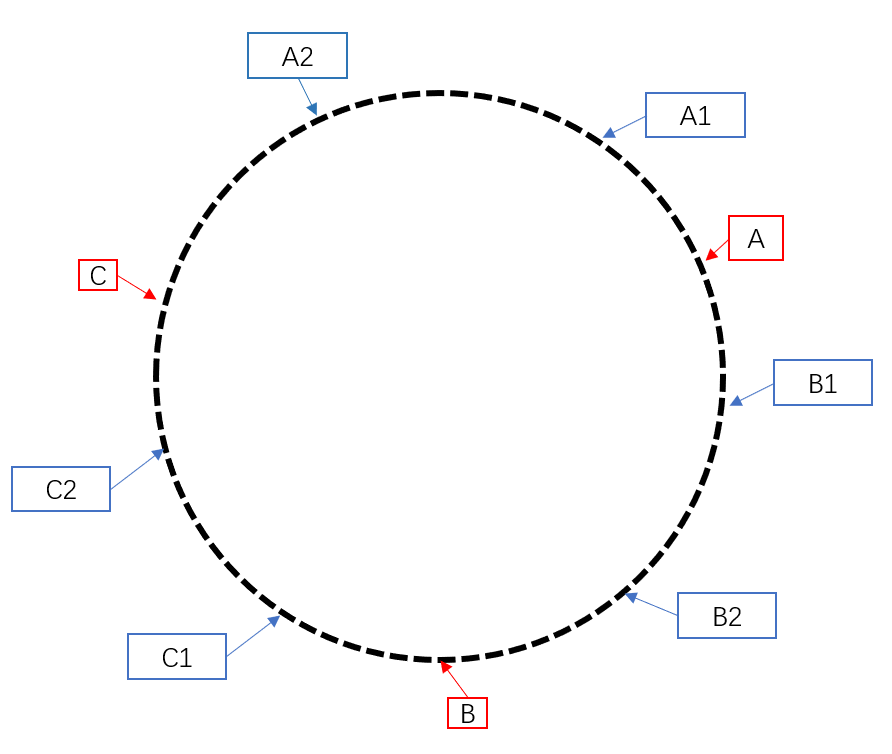
插入后，则如下图：
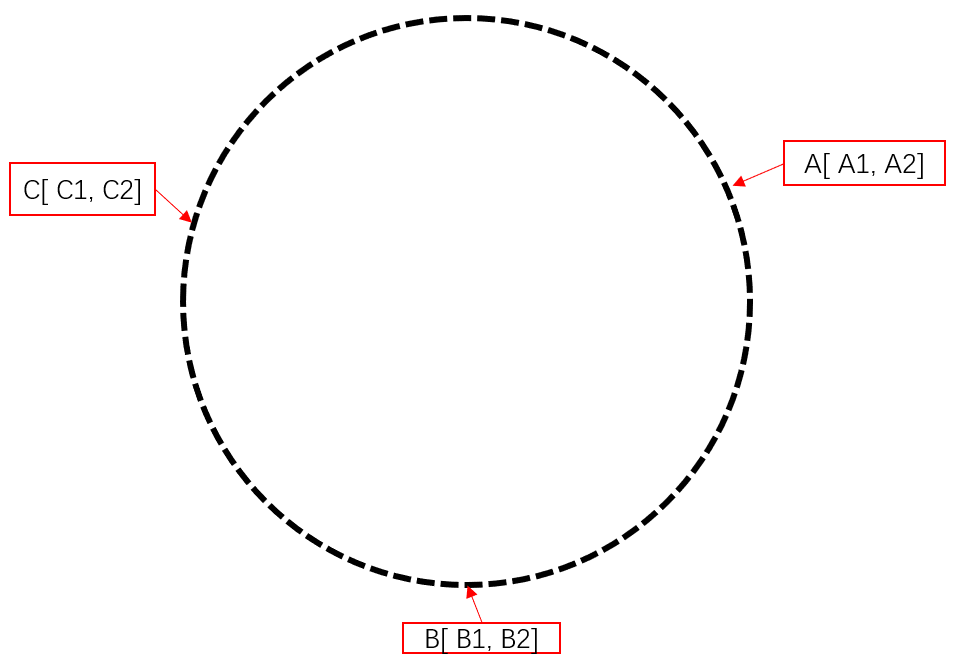
增加节点
若此时增加 D 节点，可以看到对于 A 服务器（新服务器顺时针遇到的第一个服务器），需要对其缓存进行重新排布。
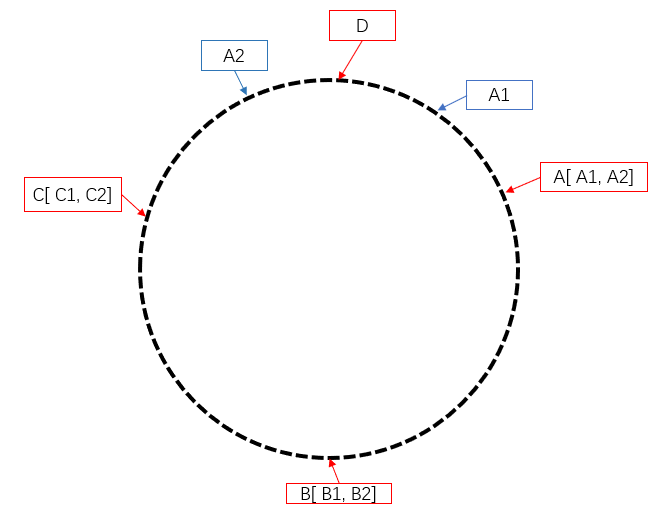
重新排布后，如下图，仅需要对 A 服务器中的缓存进行调整。
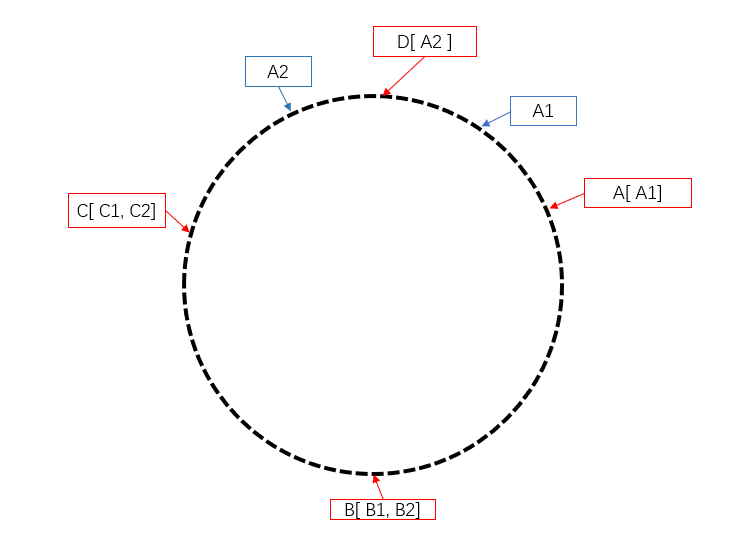
减少节点
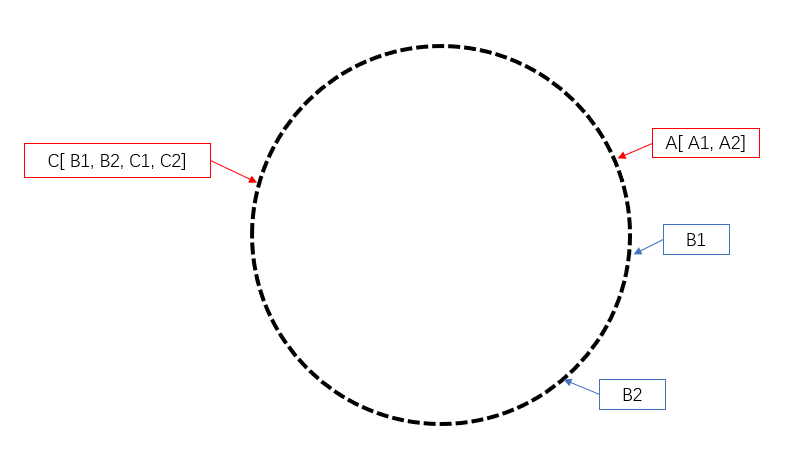
若此时，B 服务器失效，那么根据规定，B 的数据会存储至 C 中。我们仍可以访问到 B1 和 B2。
虽然在 B 服务器失效导致其中的数据要进行迁移，仅有 B 的服务器中的缓存失效需要进行迁移。
总结
采用一致性哈希的环结构使得对服务器（节点）的数量进行修改时，数据的迁移量能够达到最小，解决了全部节点的数据迁移的问题，对分布式集群来说及为有效，减小了服务器的压力。
hash 环偏斜
服务器在 hash 环中的排布可能会出现如下情况，可以看出三个节点排布的十分密集，会导致大量数据缓存在 A 服务器上。
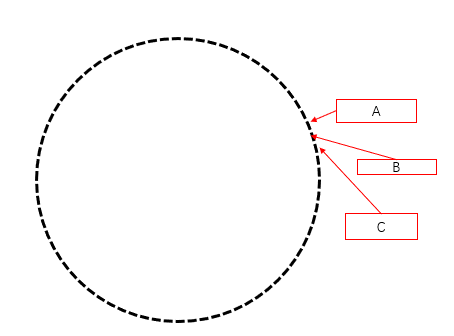
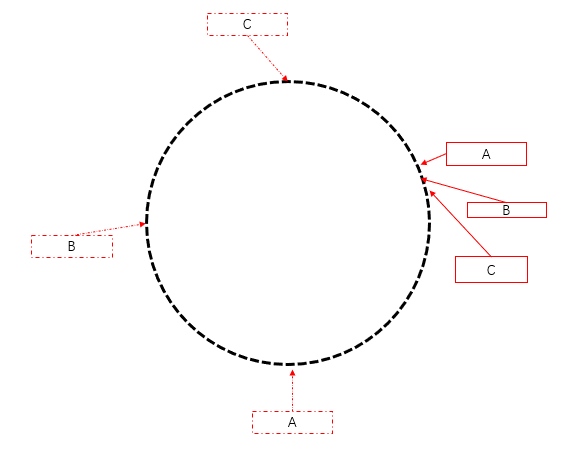
也说明了，节点在 hash 环上排布越为均匀越好，为了提高环的平衡性，在环中引入了 虚拟节点 ，使得各节点被访问量更为均匀。
