逆波兰表示法应用堆栈处理简单的四则运算

逆波兰表示法——应用堆栈处理简单的四则运算

前言

这是看到的一个小例子，再次让我感觉到了算法的魅力所在。那种对于问题的巧妙解决，让人不得不佩服前人的智慧。并结合算法逻辑，补充了相关的代码。

如果仅仅是加减乘除，可能问题的解决会非常简单，但是一旦涉及到四则运算，这种拥有一定规则限制的计算，解决起来就没那么简单了。“先乘除，后加减，先括号内再括号外，从左到右”，这是小学老师反复强调的东西。其实认为来计算，这个规则其实也十分的简单，但是机器并不是人，往往机器喜欢的东西，人会非常不喜欢，但是这种人不喜欢的东西，往往就是机器解决问题最快的方式，本文就是为了介绍这种“人们不喜欢的形式”。

1 逆波兰表示法

栈，总结起来其实就是四个字：后进先出。由于高级语言对于基本的数据结构都进行了封装，所以一般在不涉及底层的情况下，对于功能的掌握就可以满足对于该数据结构的使用了。

其实稍加注意和思考就会发现，运算表达式中的括号总是成对出现的，所以最先考虑到的就是当遇到左括号时候，将左括号压栈，遇到右括号的时候，再将一直到左括号的值出栈。但是括号只是四则运算的一部分，先乘除后加减这条规则，也是难倒了很多人，毕竟运算表达式，永远不可能将乘除写在前面给你来解决。由于这种需要准确结果的问题，贪心算法肯定是行不通的，如果一味的寻求各种规则限制，穷举各种情况的这条路肯定偏离的主方向。

为了解决这一问题，一味波兰的逻辑学家提出了一套解决方式——一种不需要括号的后缀表达式，人们称之为“逆波兰”。

1.1 中缀表达式转换成后缀表达式

既然提到了后缀表达式，那么就需要知道后缀表达式从何而来，什么是后缀表达式。

首先，后缀表达式是由中缀表达式转换而来，而中缀表达式就是我们日常写的运算表达式，即人们喜欢的形式。

举个例子：9 +（3 - 1）* 3 + 10 / 2

如上，这个例子就是一个中缀表达式。那么如何变成后缀表达式，就需要用到如下规则：

规则：从左到右遍历中缀表达式的每个数字和符号，若是数字就输出，即成为后缀表达式的一部分；若是符号，则判断其与栈顶符号的优先级，是右括号或优先级不高于栈顶符号（乘除优先于加减）则栈顶3元素一次出栈并输出，并将当前符号进展，一直到最终输出后缀表达式为止。

1.初始化栈，并将9先输出，再将 + 压栈。

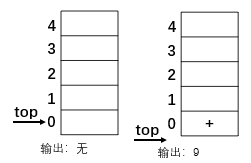
2.遇到（，依然是符号，且是左括号，压栈。接着进行）之前的内容的处理，31输出，减号压栈。

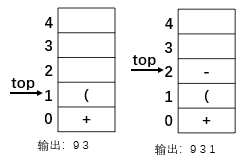
3.遇到），则栈顶一次输出，直到输出到（。继续处理到乘号，由于乘号优先级高于栈顶加号，所以不输出加号。

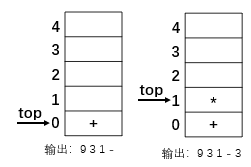
4.乘号之后是加号，而加号比乘号优先级低，所以栈中元素出栈并输出。由于栈底元素就是加号，那么需要全部输出。输出完成之后，又需要将新来的加号压栈，接着是10和2的输出，以及 / 的压栈（除号优先级高于加号）。

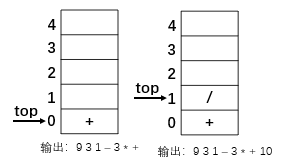
注：此处的加号是后续新来的加号，原先的加号已经输出

5.接着到了最后，栈内符号全部输出，得到 9 3 1 - 3 * + 10 2 / +

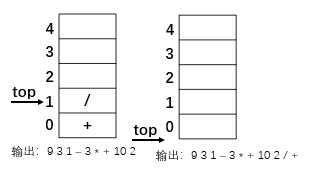
到此，中缀表达式转换完毕，得到了计算机喜欢的形式——后缀表达式。

1.2 后缀表达式计算得到结果

之所以叫做后缀表达式的原因，就是运算符号都是要在运算数字的后面出现。

和中缀表达式转换一样，后缀表达式计算得到结果也需要一定的规则，规则如下：

规则：从左到右遍历表达式的每个数字和符号，遇到是数字就压栈，遇到是符号，就将处于栈顶的两个数字出栈，进行运算，运算结果压栈，一直得到最终结果。

1.初始化栈，并将最开始的9 3 1 三个数字压栈。

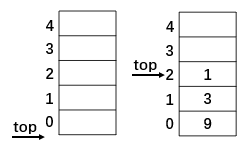
2.接着遇到减号，所以将栈顶1和3两个数字出栈，其中1作为减数，3作为被减数，即3 - 1。得到2，再将2压栈，紧接着是数字3压栈。

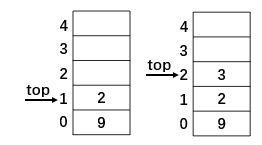
3.后续是乘号，所以3和2要出栈，进行乘法运算，得到6，再将6压栈，然后遇到加号，再将6和9出栈做加法运算得到15，再压栈。

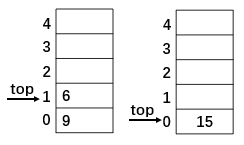
4.接下来是数字10和2压栈，遇到除号，将2作为除数，10作为被除数，做除法运算得到5，再压栈。

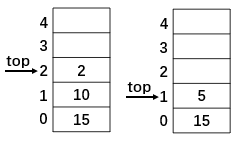
5.接下来是最后一个加号，将5和15做加法运算，并输出结果20。

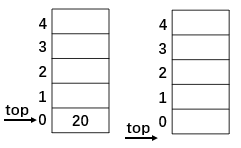
到此，这个运算表达式的结果就已经得到。

2 相关代码

# 定义运算符优先级字典
operator_priority = {'+': 1, '-': 1, '*': 2, '/': 2}
zh_to_en = {
    "（": "(",
    "）": ")",
    "【": "(",
    "】": ")",
    "「": "(",
    "」": ")",
    "『": "(",
    "』": ")",
    "《": "(",
    "》": ")",
    "[": "(",
    "]": ")",
    "<": "(",
    ">": ")",
}


def infix_to_postfix(infix_expression):
    # 创建空栈和输出列表
    operator_stack = []
    postfix_expression = []
    # 对中缀表达式进行拆分处理
    expression_list = normalized_expression(infix_expression).split()

    for item in expression_list:
        if item.isdigit():  # 如果是数字，则直接将其添加到输出列表
            postfix_expression.append(item)
        elif item == '(':  # 如果是左括号，则将其压入运算符栈
            operator_stack.append(item)
        elif item == ')':  # 如果是右括号，则要弹出运算符栈，并添加到输出列表，直到遇到左括号
            while operator_stack and operator_stack[-1] != '(':
                postfix_expression.append(operator_stack.pop())
            if not operator_stack:  # 如果栈中没有左括号，说明表达式不正确
                raise ValueError("Mismatched parentheses")
            # 左括号弹出并丢弃
            operator_stack.pop()
        else:
            # 如果是运算符
            while operator_stack and operator_priority.get(operator_stack[-1], 0) >= operator_priority.get(item):
                postfix_expression.append(operator_stack.pop())
            operator_stack.append(item)

    # 将运算符栈中剩余的运算符全部弹出，并添加到输出列表
    while operator_stack:
        postfix_expression.append(operator_stack.pop())

    # 把输出列表中的各项用空格连接成字符串
    postfix_expression_str = ' '.join(postfix_expression)
    return postfix_expression_str


def evaluate_postfix(expression):
    stack = []
    for token in expression.split():
        if token.isdigit():
            stack.append(int(token))
        elif token in '+-*/':
            b = stack.pop()
            a = stack.pop()
            if token == '+':
                stack.append(a + b)
            elif token == '-':
                stack.append(a - b)
            elif token == '*':
                stack.append(a * b)
            elif token == '/':
                stack.append(a / b)
    return stack.pop()


def normalized_expression(expression):
    """
    将书写不规范的表达式规范化，数字和运算符括号之间用空格隔开
    :param expression: 待规范表达式
    :return: 规范化后的表达式 str
    """
    expression_list = list(expression)
    output_expression = ''
    i = 0
    for a in expression_list:
        if a in zh_to_en:
            a = zh_to_en[a]
        if a.isdigit():
            # 如果是数字，看前面一个字符，如果是数字直接拼接，如果不是添加空格后再拼接当前字符
            if len(output_expression) == 0 or output_expression[-1].isdigit():
                output_expression = output_expression + a
            else:
                output_expression = output_expression + ' ' + a
        elif a == ' ':
            # 空格直接跳过
            continue
        else:
            # 其余符号先拼接空格，再拼接当前符号
            output_expression = output_expression + ' ' + a
        i += 1
        if i == len(expression):
            break
    return output_expression


if __name__ == '__main__':
    # 测试用例
    expression = " 9 +（3 - 1 )* 3 + 10 /2"
    postfix = infix_to_postfix(expression)
    result = evaluate_postfix(postfix)
    print(result)  # Output: 17

3 感悟

经过这种形式的转换，完美的得到了运算结果。且过程中仅仅是对栈进行操作，没有涉及到循环，所以时间复杂度就是O(1)。这就是算法的魅力所在，花更少的时间，解决更复杂的事，这也是逻辑学的魅力所在，巧夺天工般的处理方式。

这只是简单的带括号的加减乘除运算，而目前的计算器可以进行乘方、根号、甚至是微积分的运算。这不得不让我想去花些心思去了解计算器内部的计算逻辑。且这种表达式之间的转换，也仅仅是根据已知的规则，得到相应的结果。那么最神秘的，让人有探知欲望的还是这个规则从何而来，这必定是逻辑思维的结果，需要做进一步的探索。

算法是一个程序的灵魂所在，是真正能体现程序价值与高度的东西，需要一直的去学习，去研究，不断提高自己的思维能力。