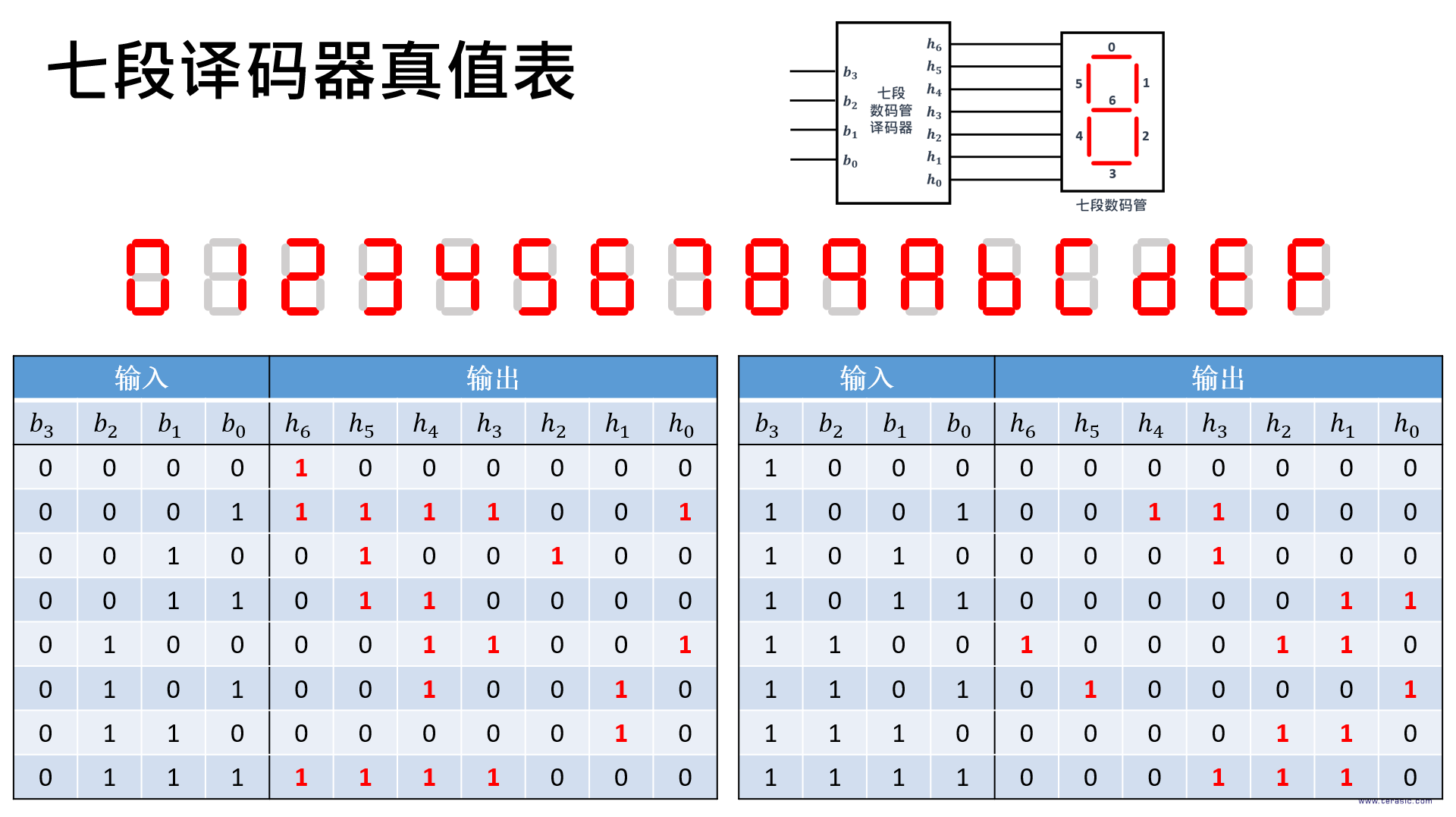
列出真值表后,就可以导出数码管每个段的逻辑表达式,从表中可以知道,当输入b3b2b1b0为0000、0001、0111、1100时,数码管的第6个段h6会被赋值为1。
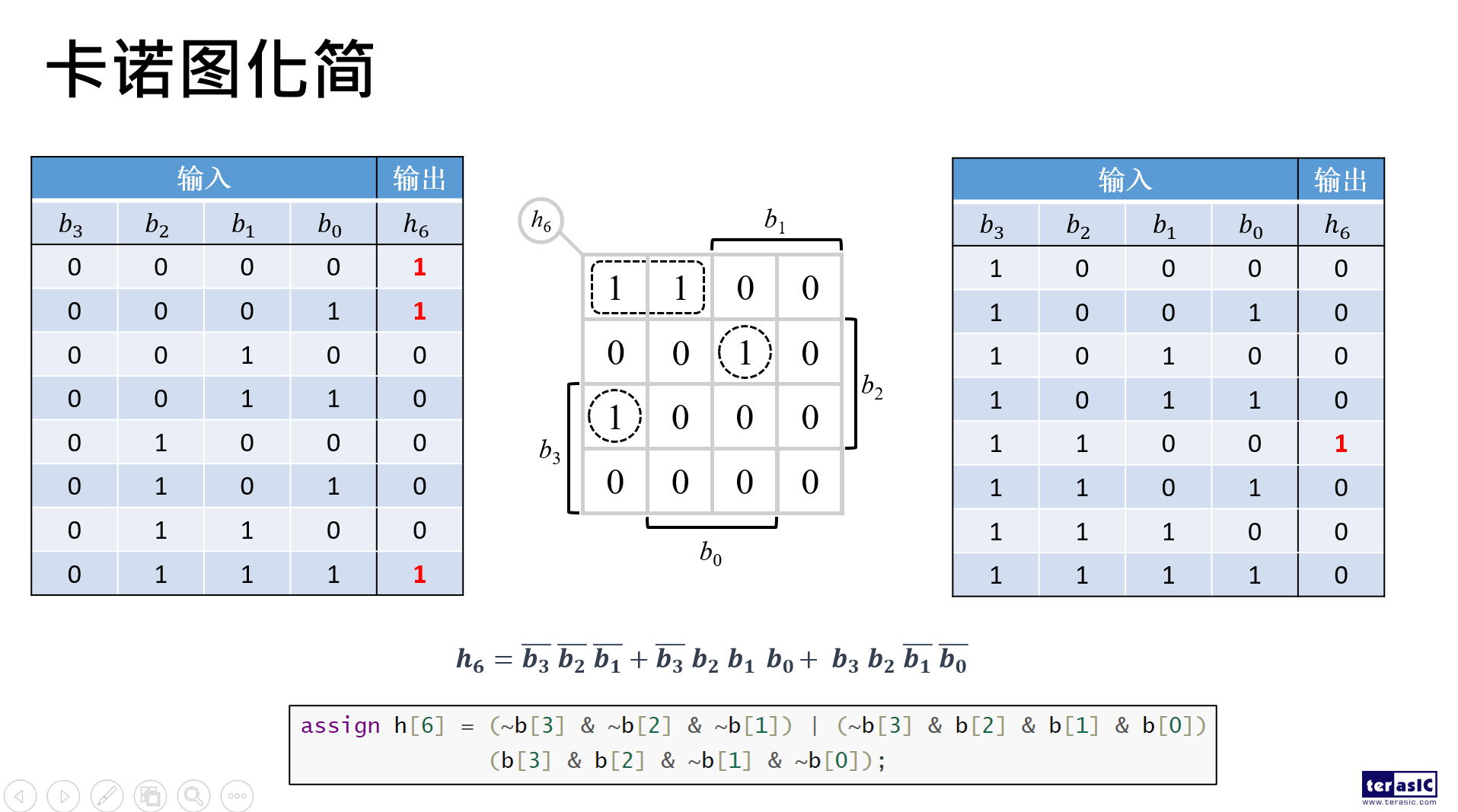
可以借助卡诺图来推导出简化的逻辑表达式,卡诺图怎么看?
我们可以看到,在方格的左上角标出了h6,表明这是数码管第6段的卡诺图;在方格的四周,每个方向都用括号括起来,并分别标示了b3、b2、b1、b0,例如,被括起来并标记b3表明这8个方格内b3的值为1,未被括起来的8个方格内b3的值为0,其余同理。
接下来我们需要在b3b2b1b0=0000处、0001处、0111处、1100处分别填入1。我们以b3b2b1b0=0000为例来介绍:b3为0,就是这两行当中的一个,b2为0,就是第一行当中的一个,b1为0,就是这两格当中的一个,最后b0为0,那我们就在第一格填入1,其余同理,继续在0001处、0111处、1100处分别填入1。其余位置填入0。
然后将相邻的填入1的方格圈成一组,注意,每一组包含的方格数必须为2n个,即1个、2个、4个、8个或16个。包围圈内的方格数要尽可能多,包围圈的数目要尽可能多。
最后将所有包围圈对应的乘积项相加,就可以得到简化的逻辑表达式了。
得到乘积项的方法与前面填入1的方式类似,我们以第一个包围圈为例来介绍,先看这个包围圈位于b3为0的8个方格内,那么b3=0,同理,它又位于b2为0的4个方格内,那么b2=0,还位于b1为0的2个方格内,那么b1=0,然后再看,b0变量被消去,就可以得出,这个包围圈的乘积项为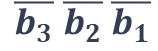
无




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步