排序算法
https://github.com/hustcc/JS-Sorting-Algorithm
排序算法是《数据结构与算法》中最基本的算法之一。
排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：
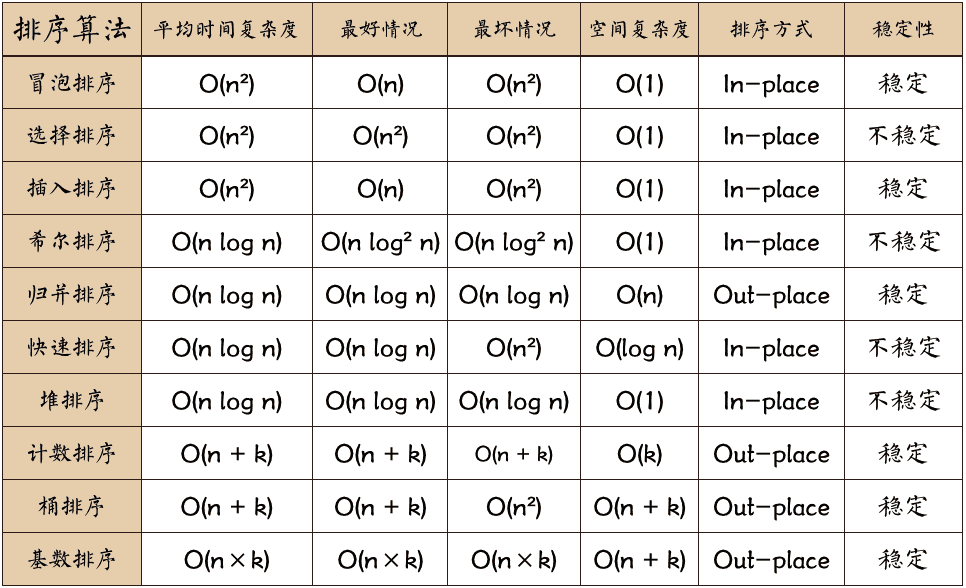
关于时间复杂度：
- 平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。
- 线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；
- O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序
- 线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。
关于稳定性：
稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。
不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。
1.冒泡排序
冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
作为最简单的排序算法之一，冒泡排序给我的感觉就像 Abandon 在单词书里出现的感觉一样，每次都在第一页第一位，所以最熟悉。冒泡排序还有一种优化算法，就是立一个 flag，当在一趟序列遍历中元素没有发生交换，则证明该序列已经有序。但这种改进对于提升性能来说并没有什么太大作用。
2.算法步骤
-
比较相邻的元素。如果第一个比第二个大，就交换他们两个。
-
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
-
针对所有的元素重复以上的步骤，除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
3.动图演示
https://github.com/hustcc/JS-Sorting-Algorithm/blob/master/res/bubbleSort.gif
4.时间
当输入是正序时最快，反序时最慢
5.代码
#include<iostream> using namespace std; template<typename T> void bubble_sort(T arr[],int len) { int i, j; for(i=0;i<len-1;i++) { for(j=0;j<len-i-1;j++) { if(arr[j]>arr[j+1]) //相邻元素对比 { swap(arr[j],arr[j+1]); //交换位置 } } } } int main() { int arr[] = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 }; int len = (int) sizeof(arr) / sizeof(*arr); bubble_sort(arr,len); for (int i = 0; i < len; i++) { cout<<arr[i]<<' '; } return 0; }
6.结果
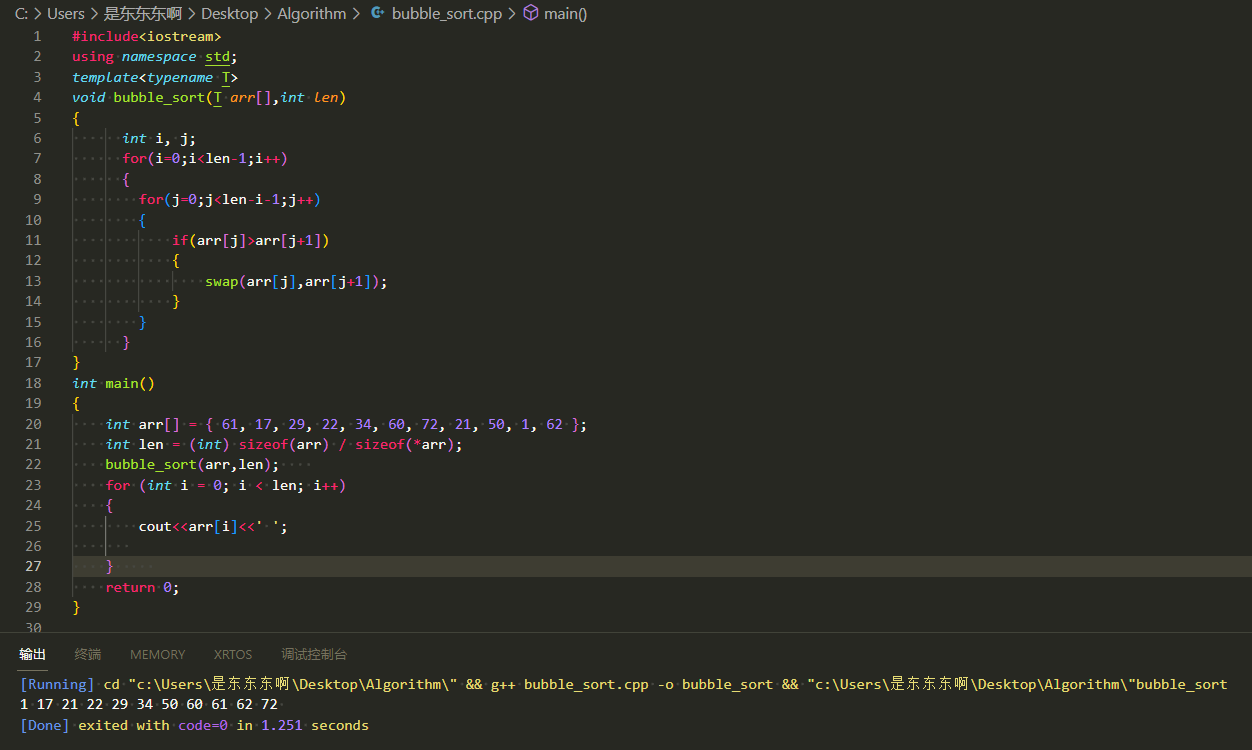
2.选择排序
选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
算法步骤
-
首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
-
再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
-
重复第二步，直到所有元素均排序完毕。
代码：
#include<iostream> #include<vector> using namespace std; template<typename T> void selection_sort(std::vector<T> &arr) { for(int i=0;i<arr.size()-1;i++) { int min = i; for(int j=i+1;j<arr.size();j++) { if(arr[j]<arr[min]) //与当前循环第一个元素比较 { min = j;//记录最小值下标 } } std::swap(arr[min],arr[i]);//与最小的元素交换位置 } } //从左向右移动，每一次拿第一个元素与其它元素比较，然后与最小的元素交换位置。 int main() { vector<int> arr = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 }; selection_sort(arr); for (int i = 0; i < arr.size(); i++) { cout<<arr[i]<<' '; } printf("hello"); return 0; }
3.插入排序
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴，但它的原理应该是最容易理解的了，因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
插入排序和冒泡排序一样，也有一种优化算法，叫做拆半插入。
-
将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
-
从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
代码：
#include<iostream> #include<vector> using namespace std; template<typename T> //vector<int> arr = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 }; void insertion_sort(std::vector<T> &arr) { for(int i=1;i<arr.size();i++) { int squence = arr[i];//从第二个数开始 int j=i-1; while ((j>=0)&&(squence<arr[j]))//每次都将拿到的数与前面所有的数比较，然后交换位置排序，类似打扑克时一张一张地抓牌然后在手里面排序 { arr[j+1] = arr[j]; j--; } arr[j+1] = squence; } } int main(int argc, const char** argv) { vector<int> arr = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 }; insertion_sort(arr); for(int i=0;i<arr.size()-1;i++) { cout<<arr[i]<<' '; } return 0; }
4.希尔排序
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。它是插入排序的高级版。
希尔排序：将无序数组分割为若干个子序列，子序列不是逐段分割的，而是相隔特定的增量的子序列，对各个子序列进行插入排序；然后再选择一个更小的增量，再将数组分割为多个子序列进行排序......最后选择增量为1，即使用直接插入排序，使最终数组成为有序。
增量的选择：在每趟的排序过程都有一个增量，至少满足一个规则 增量关系 d[1] > d[2] > d[3] >..> d[t] = 1 (t趟排序)；根据增量序列的选取其时间复杂度也会有变化，这个不少论文进行了研究，在此处就不再深究； 本文采用首选增量为n/2,以此递推，每次增量为原先的1/2，直到增量为1；
下图详细讲解了一次希尔排序的过程。
自我理解：将元素分成若干组，对每一组进行插入排序。提高了插入排序的效率。
#include<iostream> #include<vector> using namespace std; template<typename T> void shell_sort(std::vector<T> &array, int length) { for(int h=length/2;h>0;h=h/2) //按照（二分或者三分）增量将数组分成n组 { //插入排序每个小分组 for(int i=0;i<h;i++)//遍历每个小分组 { for(int j=i+h;j<length;j=j+1)//对每个小分组进行插入排序 { while((j-h)>=0&&(array[j-h]>array[j])) { std::swap(array[j-h],array[j]); j=j-h; } } } } for(int i=0;i<length;i++) { cout<<array[i]<<' '; } } int main(int argc, const char** argv) { vector<int> arr = { 61, 17, 29, 22, 34, 60, 72, 21, 50, 1, 62 }; int length = arr.size(); shell_sort(arr,length); return 0; }
参考：
原文链接：https://blog.csdn.net/jianfpeng241241/article/details/51707618
