BZOJ 1031 [JSOI2007]字符加密Cipher 后缀数组教程

1031: [JSOI2007]字符加密Cipher

Description

　　喜欢钻研问题的JS同学，最近又迷上了对加密方法的思考。一天，他突然想出了一种他认为是终极的加密办法：把需要加密的信息排成一圈，显然，它们有很多种不同的读法。例如下图，可以读作：

 

JSOI07 SOI07J OI07JS I07JSO 07JSOI 7JSOI0把它们按照字符串的大小排序：07JSOI 7JSOI0 I07JSO JSOI07 OI07JS SOI07J读出最后一列字符：I0O7SJ，就是加密后的字符串（其实这个加密手段实在很容易破解，鉴于这是突然想出来的，那就^^）。但是，如果想加密的字符串实在太长，你能写一个程序完成这个任务吗？

Input

　　输入文件包含一行，欲加密的字符串。注意字符串的内容不一定是字母、数字，也可以是符号等。

Output

　　输出一行，为加密后的字符串。

Sample Input

JSOI07

Sample Output

I0O7SJ

HINT

对于100%的数据字符串的长度不超过100000。

---

 

　　感人啊。这是第一道后缀数组的题目。早在高一寒假期间，就有学长讲过后缀数组（但当时内心当然崩溃欲绝）。后来，在高一下期，我也曾致力学习后缀数组。当时是有成效的，至少当时理解了倍增法，会解height数组，还会解一些经典题目。但时过境迁，一切都不一样了。后来，在沈阳又有学长讲授，但是也没有太大的收获（准确的说，这位一本爷的后缀数组还没有我好）。

　　然后，然后，我就忘了。

　　看来事情就是这样了。如果不练习，那很快就会忘记。

　　我们来普及一下吧。其实后缀数组，sa就是求排名第i的是谁，rank就是求i排名第几，很明显sa与rank互为反函数。也就是说，sa[rank[i]]=i，排名第rank[i]（i的排名）的是i。rank[sa[i]]=i，sa[i]（排名第i的是谁）排名第i。这是很有趣的。

　　而sa其实对应了一种有趣的树：后缀树。什么是后缀树呢？其实就是把一个串S的所有后缀串都插入一个trie，这个trie很明显与该串所有子串插入后形成的trie等价（每一个子串都是一个后缀的前缀）。但是，这样的树有O（n^2）个节点，想要实际建出明显不可能。

　　不能实际建出，于是有人就像要把这棵树压缩且不改变效果，于是有了O(n)的后缀自动机。当然，"实用"化后的后缀树也压缩过。但是，后缀树在OI中的应用并不广泛。

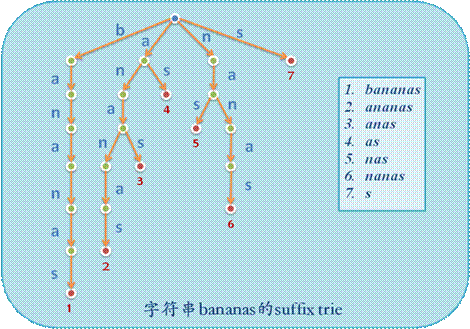
　　但是，我们也可以观察，发现可以把后缀树的末梢对应后缀从左往右写出，形成了一个数组，学名suffix_array，简称sa。当然，完整的模拟还需要一个height数组，意为sa[i-1]与sa[i]的最长公共前缀（一个不等式就可解决：height[rank[i]]>=height[rank[i-1]]-1，画图易证）。

　　如何求sa和rank呢？我们通常有2种方法，一种人称倍增O(nlog n)，另一种人称DC3 O(n)。DC3常数大得起飞，通常人们都写倍增。

　　倍增是什么？还是建议去看一看罗穗骞。

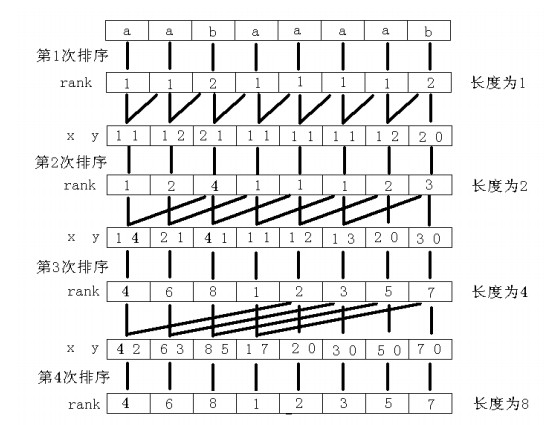
　　很有道理。1,2,4,8,16,32……最多log n次排序即可达到目标。但是一次排序怎么能是O(nlg n)的呢？于是通常会用基数排序，基数排序即是从优先级低的位到优先级高的位，对于每一位进行计数排序，中间保证是稳定的。这里排序的稳定性是指按优先级高的位排序过后，若优先级高的位相同则优先级低的位相对顺序不变。

　　计数排序即是人们俗称的桶排序（但是《算导》上说这是两种算法……迷……），把值扔到桶中，统计前缀和，然后得出排名。

　　假设给n个数基数排序，是BASE“进制”的，这些数值域为W，那么需要进行log_BASEW次计数排序。总的时间复杂度为max(n,BASE)*log_BASEW，而空间复杂度为max(n,BASE)。

　　发一波代码吧：

　　好的，我们已经会计数排序和基数排序了。我们发现，在每一次倍增时，第二关键字可以直接处理，而第一关键字需要在此之上进行一次计数排序。然后，把新的rank处理出来，因为对于每一次倍增，实时性的rank是排序所必须的value。

　　此处有一个小优化，一旦出现了多于lens个排名，那么排序已经结束，就可以退出了。

　　这是我此题的代码（也是后缀数组的模板这里小小提一下，注意一个地方的顺序，刘汝佳在此处是错的）：

/**************************************************************
    Problem: 1031
    User: Doggu
    Language: C++
    Result: Accepted
    Time:1032 ms
    Memory:4140 kb
****************************************************************/
 
#include <cstdio>
#include <cstring>
#include <algorithm>
const int S = 200010;
int bucket[S], rank[S], half[S], sa[S];
char ss[S];
void counting_sort(int range,int lens) {//In suffix_array, rank is the value, half is the radix, counting_sort and count_sort are radix sort
    for( int i = 0; i < range; i++ ) bucket[i]=0;//clear
    for( int i = 0; i < lens; i++ ) bucket[rank[half[i]]]++;
    for( int i = 1; i < range; i++ ) bucket[i]+=bucket[i-1];
    for( int i =lens-1; i>=0; i-- ) sa[--bucket[rank[half[i]]]]=half[i];//half-->sa who to the what rank 
}
bool cmp(int i,int k,int lens) {return half[sa[i]]==half[sa[i-1]]&&(sa[i]+k<lens?half[sa[i]+k]:'\0')==(sa[i-1]+k<lens?half[sa[i-1]+k]:'\0');}
void calculate(int range) {
    int lens = strlen(ss);
    for( int i = 0; i < lens; i++ ) rank[i]=ss[i], half[i]=i;
    counting_sort(range,lens); 
    for( int k = 1; k <= lens; k<<=1 ) {
        int p=0;for( int i = lens-1; i >= lens-k; i-- ) half[p++]=i;
        for( int i = 0; i < lens; i++ ) if(sa[i]>=k) half[p++]=sa[i]-k;
        counting_sort(range,lens);std::swap(rank,half);range=1;rank[sa[0]]=0;
        for( int i = 1; i < lens; i++ ) rank[sa[i]]=cmp(i,k,lens)?range-1:range++;
        if(range>=lens) break;
    }
}
int main() {
    scanf("%s",ss);
    int lens = strlen(ss);
    for( int i = lens; i < 2*lens; i++ ) ss[i]=ss[i-lens];ss[2*lens]='\0';
    calculate(128);
    for( int i = 0; i < 2*lens; i++ ) if(sa[i]<lens) printf("%c",ss[sa[i]+lens-1]);printf("\n");
    return 0;
}