解析几何 | 第 2 版

$\boldsymbol{Analytic\ Geometry}\text{ II}$

by djs.

latest update for I: 2023.07.03

latest update for II: 2023.09.26

• latest fixed: 2023.12.07

Structure

小题一般用几何。

列式方向、条件翻译、计算量预判、二级结论的应用。

资料：

• $\ell i$$nk$
• 一个不错的视频

【本文结构】

• General Solution
• 基本概念：直线、圆、椭圆、双曲线、抛物线
• 基本计算方式、列式方法
• 条件翻译
• 二级结论
• 常用模型

$\textsf{Pre-Part | General Solution}$

$\it 0.1$ 题型概述

所谓解析几何，即用代数运算与方程通过坐标系描述几何图形，虽有少量几何意义，但仍以代数运算为主。我们主要将几何条件转化为坐标、方程这样的可以计算的条件。需要注意的是，虽然解析几何理论上可以解析一切，但计算复杂度过大的计算对于在考场上的我们则无能为力。所以，寻找简化计算的方向即时解析几何的关键所在。

$$\textsf{几何}\qquad\overset{\sf 解析}{\longrightarrow}\qquad\textsf{代数}$$

解一道解析几何题，我们需要经历口个步骤：

1. 熟悉构图和基本要素（点和线），计算自由度，整体把控题目。
2. 构建要素关系网，明确控制关系。
3. 对照要素关系网的边，观察并使用二级结论进行问题的转化。
4. 根据要素关系网，预判各种变量之间关系的形式和复杂程度，考虑计算的方向，预判复杂度。
5. 考虑计算的起点，选合适的要素作为计算的主元。
6. 根据要素关系网翻译条件、表示条件，写出方程。思考能不能优化条件的表达方式减少计算量。
7. 根据前一步的预判，列出的方程消元，选择合适的计算方法，消元求解。
8. 至此圆锥曲线的部分已经完成，问题转化为其他形式（例如最值）。

先看怎么算，明确思路，盯准了再进行具体的计算，不要边想边算。如果遇到不能一眼丁真的题也要多尝试几个思路。拿到条件不要直接无脑表示，先考虑能不能进一步简化这个条件。（例如一些几何信息优化条件，比如平行 $\to$ 相似三角形、$-\frac{b^2}{a^2}$ 、椭圆几何定义）（或者可以先用仿射变换进行观察）

——沃茨 · 基硕德

$\it 0.2$ 计算相关

计算量很大。

目前没有更好的提升计算准确率的方法。

对一个题目的计算方法进行计算量预判。

【计算力提升】

1. 何为“算感”；算感平移。
2. 在纸上算，不要心算。
3. 字迹清晰，排列整齐，方便查找。
4. 小题小算，大题大算，充分利用试卷和草稿纸。
5. 提炼公式简化计算。
6. 代数式处理技巧（如平方差、因式分解）。
7. 总结常见场景最速计算方式。

$\rm I$ 基本概念、基本技法

$\it 1.1$ 直线

【直线方程】

形式	条件	方程	不适用的直线	备注
点斜式	$k$ 和点 $(x_0,y_0)$	$y=kx+y_0-kx_0$	$x=x_0$	常用（已知定点和斜率）
斜截式	$k$ 和截距 $b$	$y=kx+b$	竖线	仍然是最常用的
两点式	点 $(x_1,y_1),(x_2,y_2)$	$(y-y_1)(x_2-x_1)=(y_2-y_1)(x-x_1)$	/	极少用，因为被斜率式取代
截距式	$x,y$ 轴截距 $a,b$	$\dfrac xa + \dfrac yb=1$	竖线、横线、过原点线	了解即可
一般式	/	$ax+by+c=0$	/	少用，用于变换出公式的形式，套公式

• $ax+by+c=0\qquad\to\qquad y=-\dfrac abx-\dfrac cb$
• $ax+by+c=0$ 交 $y$ 轴与 $-\dfrac cb$，交 $x$ 轴与 $-\dfrac ca$。

【两直线位置关系】

位置关系	斜截式	一般式
平行	$k_1=k_2, b_1\not=b_2$	$a_1b_2=a_2b_1\quad\text{and}\quad a_1c_2\not=a_2c_1$
相交	$k_1\not=k_2$	$a_1b_2\not=a_2b_1$
垂直	$k_1k_2=-1$	$a_1a_2+b_1b_2=0$

• 直线 $ax+by+c=0$ 的一个法向量为 $\vec m=(a, b)$。

【点与直线的位置关系】

• 对于点 $(x_0,y_0)$ 和线 $ax+by+c=0$ ：
• 若 $ax_0+by_0+c>0$ 则点在直线下方。
• 若 $ax_0+by_0+c<0$ 则点在直线上方。
• 故若将 $A,B$ 两点带入方程，得到的结果同号则两点在直线同侧；若异号则在直线异侧。

$\it 1.2$ 圆

【基本概念】

• 标准方程：$(x-a)^2+(y-b)^2=r^2$，描述一个圆心为 $(a, b)$，半径为 $r$ 的圆。
• 一般方程：$x^2+y^2+Dx+Ey+F=0$，其中 $D^2+E^2-4F>0$，将其配方后即可得到标准形式。其中圆心 $(-\dfrac D2, -\dfrac E2)$，$r^2=\dfrac14(D^2+E^2-4F)$

【圆与直线的位置关系】

• 用点到直线的距离公式计算圆心与直线的距离，以此判断圆与直线的相交 / 相切 / 相离。
• 同样在判断圆与圆的位置关系时，计算圆心之间的距离并与半径比较即可（$r_1+r_2, |r_1-r_2|$ 等）。
• 判断点与圆的位置关系时，可以将点带入圆的方程（例：若 $<0$ 则在圆内）

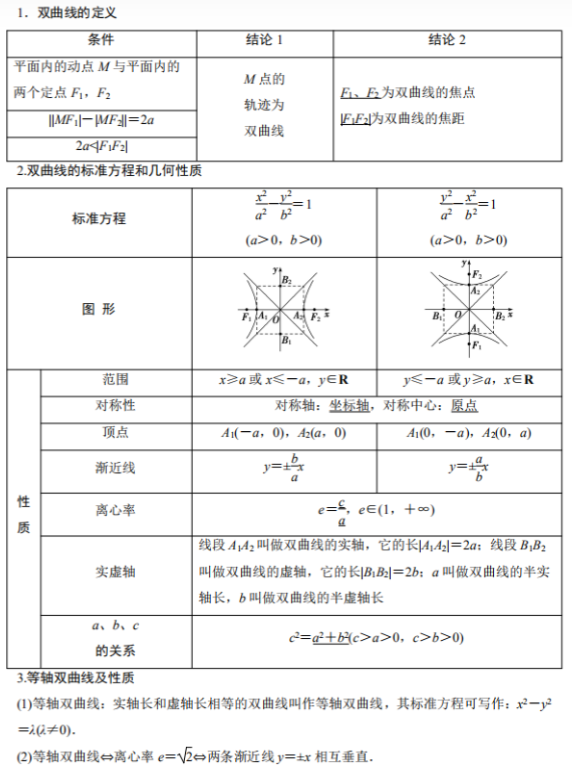
$\it 1.3$ 椭圆

【基本性质】
椭圆的第一定义：平面上到两点 $F_1(-c, 0), F_2(c, 0)$ 的距离之和为 $2a$ 的点构成的曲线为椭圆，其标准方程为 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$。其中 $c=\sqrt{a^2-b^2}$。

椭圆的第二定义：到椭圆一侧焦点 $F$ 的距离与到直线 $x=\pm\dfrac{a^2}{c}$（在坐标系 $y$ 轴同侧）的距离之比为定值 $e$ 的点构成的轨迹为椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$。（$\dfrac{|PF|}{|PH|}=e$）

• 焦半径公式：$P$ 在椭圆上，$|PF_1|=a-e\cdot x_P$

椭圆的第三定义：平面内动点到 $A(-a, 0), B(a, 0)$ 的直线的斜率之积为常数 $-\dfrac{b^2}{a^2}$ 的点构成的轨迹为椭圆，其中 $e$ 为其离心率。

• 设 $A, B, P$ 是椭圆上不同的三点，其中 $A, B$ 关于原点对称，那么恒有 $k_{PA}\cdot k_{PB}=-\dfrac{b^2}{a^2}$。
• 看到斜率之积为定值想第三定义。

【基本计算方式】

• 直线与椭圆交：将直线与椭圆联立得到一个关于 $x$ 或关于 $y$ 的二次方程，可通过判断 $\Delta$ 的正负判断直线与椭圆相交 / 相切 / 相离。（$\Delta=a^2A^2+b^2B^2-C^2$，$\Delta>0$ 表示与直线相交）
• 注：若弦过椭圆的交点，那么这条弦叫焦点弦；若焦点弦垂直于交点所在的椭圆的对称轴，那么这条焦点弦叫通径（通径长度 $\ell=\dfrac{2b^2}{a}$）。

$\it 1.4$ 双曲线

第一定义：平面上到两点 $F_1(-c, 0), F_2(c, 0)$ 的距离的差（绝对值）为定值的点构成的曲线为双曲线。

第二定义（焦准）：到双曲线一侧焦点 $F$ 和同侧准线 $x=\pm\dfrac{a^2}{c}$ 的距离值比为定值 $e$（$\dfrac{|PF|}{PH}=e$）的点构成的图形为双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$。

第三定义（斜率式）：设 $A, B, P$ 是双曲线上不同的三点，其中 $A, B$ 关于原点对称，那么恒有 $k_{PA}\cdot k_{PB}=\dfrac{b^2}{a^2}$。

$\it 1.5$ 抛物线

! image 抛物线

• 标准式：$y^2=2px$（开口朝右边的躺着的抛物线）
• 参数式：$x=\dfrac{y^2}{2p}$（以一次的项为控制变量）
• 第二定义（焦准）：焦点 $F(\dfrac p2, 0)$，准线 $\ell:x=-\dfrac p2$。
• 极坐标式：$\rho=\dfrac{p}{1-\cos\theta}$

抛物线上任意一点 $A$ 到抛物线焦点 $F(\dfrac p2, 0)$ 的距离等于其到抛物线准线 $\ell:x=-\dfrac p2$ 的距离。

【基础二级结论】

• 设抛物线 $y^2=2px$ 焦点为 $F$，抛物线的一条弦为 $AB$，其中 $A(x_1, y_1)$，$B(x_2, y_2)$。
• 若 $\ell_{AB}$ 过 $x$ 轴上的定点，则 $y_1y_2$ 为定值。
• 若 $k_{AB}$ 一定，则 $y_1+y_2$ 为定值。

$\it 1.6$ 平面对象运算方法

【基本条件表示】

• 夹角公式：$\tan\langle \ell_1, \ell_2\rangle=|\dfrac{k_1-k_2}{1+k_1k_2}|\qquad\theta\in[0, \dfrac\pi2]$
• 距离公式：$|AB|=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}$
• $P(x_0, y_0)$ 到直线 $\ell:ax+by+c=0$ 的距离：$d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}=\dfrac{|kx_0+b-y_0|}{\sqrt{1+k^2}}$
• 弦长公式：$|AB|=\sqrt{1+k^2}\cdot|x_A-x_B|$
• 平行线 $\ell_1:ax+by+c_1=0$ 与 $\ell_2:ax+by+c_2=0$ 之间的距离：$d=\dfrac{|c_2-c_1|}{\sqrt{a^2+b^2}}$

【直线运算技巧、直线系方程】

• 与 $ax+by+c=0$ 平行的直线：$ax+by+c'=0$
• 与 $ax+by+c=0$ 垂直的直线：$bx-ay+c'=0$
• 过定点 $(x_0, y_0)$ 的直线：$a(x-x_0)+b(y-y_0)=0$ 或 $y=k(x-x_0)+y_0$
• 过两直线交点的直线方程：$a_1x+b_1y+c_1+\lambda(a_2x+b_2y+c_2)=0$（注意取不到 $\ell_2$）
• 直线有关的对称问题：点 $(x_0,y_0)$ 关于线 $ax+by+c=0$ 对称 $\to$ $(y_0-\dfrac{2a}{a^2+b^2}(ax_0+by_0+c),x_0-\dfrac{2b}{a^2+b^2}(ax_0+by_0+c))$
• 线关于点对称：降维求解、夹角公式
• 反射问题通法：作对称
• 三角形重心坐标公式： $G(\dfrac13(x_1+x_2+x_3),\dfrac13(y_1+y_2+y_3))$
• 三角形内心边元形式：$a\vec{OA}+b\vec{OB}+c\vec{OC}=0$

【圆运算技巧、圆系方程】

• 判断直线和圆的位置关系：距离公式计算圆心到直线的距离。【取值问题找圆心，勾股定理全搞定】
• 双切线：使用极点极线结论。
• 切线相关
  • 非同心相交两圆方程方程相减，所得直线为公共弦所在直线。
  • 非同心相切（内切外切）两圆方程方程相减，所得直线为过两圆切点的公切线。
  • 过圆 $(x-a)^2+(y-b)^2=r^2$ 上一点 $P(x_0, y_0)$ 的圆切线方程为 $(x_0-a)(x-a)+(y_0-b)(y-b)=r^2$。（过圆 $x^2+y^2=r^2$ 上一点 $P(x_0, y_0)$ 的圆切线方程为 $x_0x+y_0y=r^2$）
• 【圆系方程】
  • 过直线 $Ax+By+C=0$ 与圆 $x^2+y^2+Dx+Ey+F=0$ 交点的圆系方程为 $x^2+y^2+Dx+Ey+F+\lambda(Ax+By+C)=0$。
  • 过两圆 $C_1:x^2+y^2+D_1x+E_1y+F_1=0$ 与 $C_2:x^2+y^2+D_2x+E_2y+F_2=0$ 的交点的圆系方程为 $C_1+\lambda C_2$（此方程不含 $C_2$）。
• $x\cos\theta+y\sin\theta+1=0$ 表示单位圆的所有切线。
• 阿氏圆：构造相似
  • 已知恒有 $\dfrac{|AB|}{|AC|}=k$
  • 
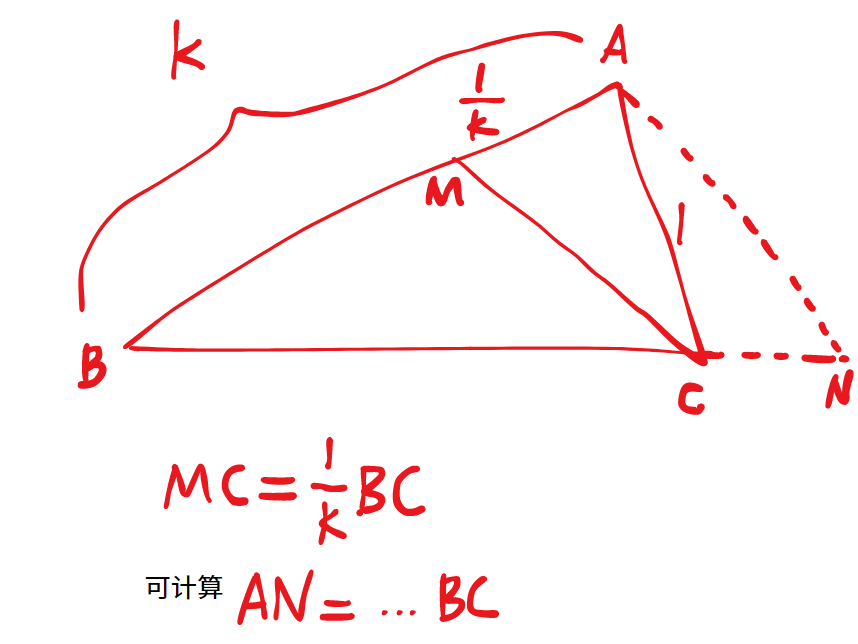
  • 已知第三边的比例且角平分线：定点轨迹为阿氏圆
• 圆生成的函数：$f(x)=\sqrt{-x^2+bx+c}$（一般是半圆）。
• 圆的斜率式：以 $A(x_1,y_1),B(x_2,y_2)$ 为直径的端点的圆方程为 $(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0$ （用垂直证明）。
• 圆幂定理：主打相似。

$\rm II$ 列式方向

$\it 2.1\ \textsf{General solution}$ ——联立

“解析”本质上还是对方程的联立，由若干方程联立到一起的方程组对自由度进行消解，而对方程组的巧妙处理可以大幅降低计算量。解析几何用方程的联立，架起变量之间的桥梁。有以下几个工具：

• 韦达定理（两根关系）
• 判别式（根是否存在）
• 方程的联立、消元
• 方程之间加减乘除的变换
• 其他变换

【列式步骤】

1. 明确研究对象，计算自由度，理清要素关系网（对象之间的控制关系）。
2. 观察要素关系网，预估每一步计算的复杂度，利用各种二级结论，预估变量之间的约束形式和复杂程度（称之边权阻值）。
3. 综合计算复杂程度和二级结论，在要素关系网中选取合适的起点设出主元。
4. 根据控制关系翻译条件，列出式子。
5. 联立方程消元求解。
6. 最后结合问题进行下一步求解。
   • 最值问题回归到函数化或多变量求最值上。

【常用 $\textsf{General Solution}$】

• 【预知】利用各种二级结论预见变量之间的限制关系的形式和复杂程度，如用“手电筒模型”预见 $k_1+k_2$ 为定值。
• 【对称】出现对称结构的条件或相同性质的对象（相同性质多解，如两点都是同一直线与曲线的交点）可以考虑联立研究方程组的性质，套用韦达或方程组变换。
  • 研究不对称的式子可以刻意构造对称（如求 $\dfrac{x_1}{x_2}$ 的范围可以转化为 $\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}$）
  • 研究不对称构造元素的时候，可以构造出另一边的对象呈现出对称，进行研究。
• 【判定】将不同的自由度转化，借此将复杂的限制条件转化为简单易处理的条件。
• 【丁真】利用各种二级结论猜测所求定点位置，所求不等式取最值的取等条件。

不要忘了最基本的代换 $y=kx+m$。

$\it 2.2$ 变量的表示、基本运算

gs：设线一般是用来联立的，设点一般是有很好的点驱动关系。一般情况下以设线联立为主。根据需要来。

设点之参数方程：

• 将一个点 $A(x, y)$ 写成 $A(a\cos\theta, b\sin\theta)$，这样就可以做到只用一个变量表示一个点。双曲线是 $A(a\sec\theta, b\tan\theta)$。
• 配合三角恒等变换。

直线表示：

• $y=kx+m, x=ky+m$（正设和反设，可能有计算量的差别）
• $y=\dfrac{y_2-y_1}{x_2-x_1}(x-x_1)+y_1$ 两点式
  • $y=\dfrac{y_2-y_1}{x_2-x_1}(x-\dfrac{x_1+x_2}{2})+\dfrac{y_1+y_2}{2}$ 刻意构造对称
• $mx+ny=1$ 用于齐次化的设法$\begin{cases}x=x_0+r\cos\theta\\y=y_0+r\sin\theta\end{cases}$ 定点长度相关（例如圆上的点）

抛物线一般用点参，例如 $A(y_1^2, y_1)$。

直线相交：利用斜率相等，如 $\dfrac{y_P-y_A}{x_P-x_A}=\dfrac{y_P-y_B}{x_P-x_B}$。

【非对称条件处理方法】

1. 涉及定点问题时先猜出定点带入求解。
2. 由韦达定理建立两根和积关系式带入化简。
3. 以 $x_1$ 或 $x_2$ 为主元进行消元化简。
4. 涉及 $k_1\cdot k_2=-\dfrac{b^2}{a^2}$ 的问题使用第三定义进行转化。
5. 利用点在圆锥曲线上的方程进行化简（$P(a\cos\alpha, b\sin\alpha)$）
6. 刻意构造对称（如 $\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}, y=k(x-\dfrac{x_1+x_2}{2})+\dfrac{y_1+y_2}{2}$）。

刻意构造对称，例如使用两点式（或点斜式）时可以挑选两点的中点，例如 $y=k(x-\dfrac{x_1+x_2}{2})+\dfrac{y_1+y_2}{2}$，方便使用韦达。

$\it 2.3$ 处理方向 1 - 韦达

最常规的方法。

【基本内容】
韦达定理：已知二次方程 $Ax^2+Bx+C=0$，两根为 $x_1, x_ 2$，则有 $x_1+x_2=-\dfrac BA, x_1x_2=\dfrac CA$

即设出线的解析式，与椭圆联立化为与 $x$ 或 $y$ 相关的二次方程，进而得到交点横纵坐标的和差信息（$x_A+x_B=..., x_Ax_B=...$），利用所得信息进行进一步解题。

通常有两种出发方向：点驱动（设点）与线驱动（设线）。

如果所求式对称，那么就可以用韦达获得交点的和与乘积的关系式，但该方法的缺点是较为传统，有的时候计算量较大。

$$\left<\begin{aligned} y=kx+m\\\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \end{aligned}\right>\Rightarrow \left<\begin{matrix}(a^2k^2+b^2)x^2+2a^2kmx+a^2(m^2-b^2)=0 \\ \\ (a^2k^2+b^2)y^2-2b^2my+b^2(m^2-a^2k^2)=0\end{matrix}\right>$$

上式是椭圆与直线 $y=kx+m$ 的联立，联立双曲线时将所有 $b^2$ 替换为 $-b^2$ 即可。

（加速计算）点乘双根：$a_2x^2+a_1x+a_0 = a_2(x_1-x)(x_2-x)$，将 $x$ 赋值某常数 $m$ 后直接带入左边的式子可以方便地计算 $a_2(m-x_1)(m-x_2)$ 的值。

【硬解定理】

• 椭圆
  • $(a^2k^2+b^2)x^2+2a^2kmx+a^2(m^2-b^2)=0$
  • $(a^2k^2+b^2)y^2-2b^2my+b^2(m^2-a^2k^2)=0$
  • 由韦达定理即可求解 $x_1+x_2$，$x_1x_2$，$y_1+y_2$ 以及 $y_1y_2$。
  • $x_1y_2+y_1x_2=\dfrac{-2a^2b^2k}{a^2k^2+b^2}$
  • $|x_1-x_2|=\dfrac{2ab}{a^2k^2+b^2}\sqrt{a^2k^2+b^2-m^2}$
  • $|y_1-y_2|=|k|\cdot|x_1-x_2|=\dfrac{2ab|k|}{a^2k^2+b^2}\sqrt{a^2k^2+b^2-m^2}$
• 双曲线
  • $(a^2k^2-b^2)x^2+2a^2kmx+a^2(m^2+b^2)=0$
  • $(a^2k^2-b^2)y^2+2b^2my-b^2(m^2-a^2k^2)=0$
  • 计算 $|x_1-x_2|$ 时注意根号下的式子的正负。

trick：二次方程已知一根可以直接用韦达定理解另一根（如果二次方程已知一根或有特殊性质可以考虑直接解）

【反设】

• 设 $x=ky+m$（注意此时的 $k$ 是真正斜率的倒数）
• 将 $a$ 与 $b$ 的地位调换，$x$ 与 $y$ 的地位调换即可。
• 如 $(b^2k^2+a^2)y^2+2b^2kmy+b^2(m^2-a^2)=0$。

【抛物线】

• 较为 trivial
• $\begin{cases}y^2=2px\\x=ky+m\end{cases}\to y^2-2pky-2pm=0$。

$\it 2.4$ 处理方向 2 - 方程组变形

【$\sf gs$】
如何快速解联立的方程组？

若存在形式非常相近或出现相同结构的方程，那么就可以考虑对方程之间进行整体的变换，例如作差、作商等等。这样得到的方程的形式可能优于原方程，也可以做到构造对称。注意方程组的自由度问题，有多少个方程就要解出多少个条件。

【经典模型】定比点差法

• 用于处理中点弦、定比分弦等等。
• 设出椭圆上两点 $A(x_1, y_1), B(x_2, y_2)$，得到椭圆方程 $\begin{cases}\dfrac{x_1^2}{a^2}+\dfrac{y_1^2}{b^2}=1\\\dfrac{x_2^2}{a^2}+\dfrac{y_2^2}{b^2}=1\end{cases}$，两者做差后运用平方差公式可以得到中点弦的二级结论之一 $k_{AB}\cdot k_{OM}=-\dfrac{b^2}{a^2}$。
• 其变式为可以表示线段的定比分点（按某个比例取得的点），即将某一个式子乘 $\lambda^2$（$\lambda$ 为比例）之后做差相减，得到 $\dfrac{(x_1-\lambda x_2)(x_1+\lambda x_2)}{a^2}+\dfrac{(y_1-\lambda y_2)(y_1+\lambda y_2)}{b^2}=1-\lambda^2$。
• 其他应用有待研究。

【抛物线点参解析式】（点差）
初中全靠这一条公式做二次函数......

• 对于抛物线 $y=ax^2+bx+c$ 上的两点 $x_M, x_N$，有 $\ell_{MN}:y=[a(x_M+x_N)+b]x-ax_Mx_N+c$。
• 对于抛物线 $y^2=2px$ 上的两点 $y_M, y_N$，有 $\ell_{MN}:x=\dfrac{x_M+x_N}{2p}y-\dfrac{x_Mx_N}{2p}$。

【对偶式】

• 黄金 $n$ 角的本质：对偶式 $\alpha x+\beta y\lrarr\beta x-\alpha y$。
• 构造对偶式，如 $x_1y_2+x_2y+1$，使之出现 $x, y$ 的平方项，带入椭圆方程。

$\it 2.5$ 处理方向 3 - 齐次化处理 | 配合平移

【齐次化】

• 将直线方程写成 $mx+ny=1$ 的形式，用“1 的妙用”（本质是调节次数使之齐次化）将其带入二次曲线式中联立，得到关于 $\dfrac{y}{x}$ 的二次方程（即到原点连线的斜率），获得 $k_1+k_2$ 与 $k_1\cdot k_2$ 的信息。为应对目标直线交点不在原点的情况，通常配有坐标系平移的操作。
• 处理过定点两直线斜率的和或积信息，常用于一些定点的证明。
• 平移后记得要变回来！

$\it 2.6$ 用参数方程表示圆锥曲线的弦

椭圆及双曲线点参解法（三角函数表示）：by chair.

对于椭圆：

$$A(a\cos\alpha, b\sin\alpha)\xlongequal{m_A\gets\tan\frac\alpha2} A(a\cdot\dfrac{1-m_A^2}{1+m_A^2}, b\cdot\dfrac{2m_A}{1+m_A^2}) \\ B(a\cos\beta, b\sin\beta)\xlongequal{m_B\gets\tan\frac\beta2}B(a\cdot\dfrac{1-m_B^2}{1+m_B^2}, b\cdot\dfrac{2m_B}{1+m_B^2}) \\ \rArr \ell_{AB}:ay(m_A+m_B)-bx(m_Am_B-1)=ab(m_Am_B+1)$$

对于悲伤的双曲线：

$$A(a\sec\alpha, b\tan\alpha)\xlongequal{m_A\gets\tan\frac\alpha2} A(a\cdot\dfrac{1+m_A^2}{1-m_A^2}, b\cdot\dfrac{2m_A}{1-m_A^2}) \\ B(a\sec\beta, b\tan\beta)\xlongequal{m_B\gets\tan\frac\beta2}B(a\cdot\dfrac{1+m_B^2}{1-m_B^2}, b\cdot\dfrac{2m_B}{1-m_B^2}) \\ \rArr \ell_{AB}:ay(m_A+m_B)-bx(m_Am_B+1)=ab(m_Am_B-1)$$

对于抛物线 $y^2=2px$：$\ell:(y_1+y_2)y-y_1y_2=2px$

$\it 2.7$ 注意事项

直接设直线时涉及变量取值范围时必查 $\Delta$。

$\rm III$ 条件翻译

$\it 3.1$ 坐标系中的基本对象处理

• 直线
  • 两直线交点：$\dfrac{y_0-y_1}{x_0-x_1}=\dfrac{y_0-y_2}{x_0-x_2}$（斜率式）（常用）
  • 平行：$k_1=k_2$ 或 $\vec m=\lambda\vec n$。
  • 垂直：$k_1k_2=-1$ 或 $\vec m\cdot\vec n=0$。
  • 直线与圆锥曲线的位置关系：判 $\Delta$ 正负。
  • 直线与圆锥曲线相交（属于较复杂的关系）：
    • 获得点坐标的和、积：联立韦达。
    • 获得到某个定点的直线斜率的关系（和、积）：联立构造齐次化，配合平移。
• 角度
  • 斜率 $k=\tan\theta$
  • $\tan\theta=\dfrac{k_1-k_2}{1+k_1k_2}$，转化成斜率的信息（比如说接着用齐次 - 平移）
  • 向量夹角公式数量积。
  • 运用公式中所带的三角函数。
  • 用特殊手段证明角度相等（如相似等几何关系）
  • 特殊角度：特殊手段（如焦点三角形相关、阿基米德三角形）
• 线段中点：$\left(\frac12(x_1+x_2), \frac12(y_1+y_2)\right)$；
  • 线段定比分点：向量。
• 圆
  • 直线与圆的位置关系：计算圆心到直线的距离（套公式）。
  • 极点极线相关结论。
• 长度
  • 一般的长度：两点距离公式。
  • 弦长：$\ell=\sqrt{k^2+1}|x_1-x_2|$。
  • 点 $(x_0, y_0)$ 到直线 $Ax+By+C=0$ 的距离公式 $\ell=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$
  • 特殊长度：特殊方法（如焦半径）
• 两点之间斜率：$k=\dfrac{y_2-y_1}{x_2-x_1}$。
• 焦点三角形的顶角：$S=b^2\cdot\tan\dfrac\theta2$。
• 三点共线：$A, B, C$ 共线，则 $k_{AB}=k_{AC}$（随意各选两点即可）（列斜率式）

$\it 3.2$ 几何条件代数化方向

• 重心：坐标公式（加起来除 $3$）
• 三角形的面积
  • 基础：$S=\dfrac12ah$（弦长 + 距离公式）
  • 铅锤法
  • 向量叉积 $S=\dfrac12|x_1y_2-x_2y_1|$
    • 向量叉积形式的四边形对角线面积公式：已知原点为 $O$ 的坐标系内四边形 $ABCD$，则 $S_{ABCD}=\dfrac12[(x_A-x_C)(y_B-y_D)+(x_B-x_D)(y_C-y_A)]$（分为 $S_{\Delta OAB}, S_{\Delta OBC}, S_{\Delta OCD}, S_{\Delta ODA}$ 四个三角形然后叉积）
    • 四边形的面积：拆成两个三角形；对角线垂直型 $S=\dfrac12ab$；平行四边形 $S=2ab\sin\theta$。
  • 仿射变换
  • 特殊面积：特殊处理（如焦点三角形）
• 同一条直线上相邻长度的比：
  1. 转化为横或纵坐标比
  2. 向量表示
  3. 仿射变换
• 各种向量条件：坐标表示，基本用不到几何意义
• 点和直线的变换
  • 等腰三角形 / 垂直平分线：垂直 + 中点
  • 点与点关于某直线对称：垂直 + 中点
• 角平分线：
  1. 水平或竖直：斜率 $k$ 取反
  2. 斜线：用夹角公式，或变成长度用角平分线定理
  3. 椭圆的光学性质相关（焦点三角形）

$\rm IV$ 二级结论与常用模型

熟练掌握和使用二级结论可以掌控全局，有效帮助预判计算方向和计算量。

【二级结论】

• 有些题在动笔之前就被丁真薄纱了。

$\it 4.1$ 仿射变换与斜率

【仿射变换基本概念】

• 将原坐标系的所有点的横纵坐标进行等比例放缩，如 $\begin{cases}x\to ax\\y\to by\end{cases}$。一般放缩为圆或反比例函数（$y=x$）等易于处理的图形。
• 性质：
  1. 斜率成比例变化（线性）。
  2. 面积成比例变化（线性）。
  3. 点线相对位置关系不变，同一直线上的线段长比例不变（包括向量加减运算）。
• 求奇怪面积的时候可以用仿射变换。
• 参数方程 $A(a\cos\alpha, b\sin\alpha)$ 本质也是仿射变换。

【椭圆第三定义相关】

• 平面上 $A(-a, 0), B(a, 0)$ 两点，平面上一动点 $P$ 到两点直线斜率之积 $k_{PA}\cdot k_{PB}=-\dfrac{b^2}{a^2}$，则 $P$ 的轨迹为椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$。
  • 该结论经仿射变换为圆后易证。事实上，对于椭圆上任意关于原点对称的两点，该结论都适用。
• 斜率之积 $-\dfrac{b^2}{a^2}$ 十分特殊，其经仿射变换为圆后将变为 $-1$，即两直线垂直。
• 椭圆中点弦：经仿射变换后变为圆中垂径定理模型（$k_{AB}\cdot k_{OP}=-\dfrac{b^2}{a^2}\quad\to\quad k_{A'B'}\cdot k_{OP'}=-1$）

【衍生结论 & 方法体系】

• 若 $A(x_1, y_1), B(x_2, y_2)$ 是椭圆 $\Gamma:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 上的两个动点，满足 $k_{OA}\cdot k_{OB}=-\dfrac{b^2}{a^2}$（也就是仿射为圆后 $OA'\perp OB'$），那么：
  1. $S_{\Delta AOB}=\dfrac{S_{\Gamma}}{2\pi}=\dfrac12ab$，$x_1^2+x_2^2=a^2, y_1^2+y_2^2=b^2$。
  2. 若椭圆上一点 $M$ 满足 $\vec{OM}=\lambda\vec{OA}+\mu\vec{OB}$，则 $\lambda^2+\mu^2=1$；若平面内一点 $N$ 满足 $\vec{ON}=\lambda\vec{OA}+\mu\vec{OB}$，则 $N$ 点的轨迹是 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=\lambda^2+\mu^2$。
• 对于双曲线，将其仿射为反比例函数后对应的有效斜率积为 $\dfrac{b^2}{a^2}$（且需要将仿射后的 $x^2-y^2=1$ 旋转 $45^\circ$ 变为函数 $y=\dfrac1x$）。过双曲线
  • 双曲线中的面积定值：过双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 上一点 $P(x_0, y_0)$ 作两条分别平行于渐近线的直线，围成的平行四边形面积为定值 $S=\dfrac12ab$。

【其他斜率相关二级结论】

• 椭圆上 $A, B$ 两动点，满足 $\ell_{OA}\perp\ell_{OB}$，点 $P$ 是原点 $O$ 关于弦 $AB$ 的垂足，则 $P$ 的轨迹是以原点为圆心，半径为 $\dfrac{a^2b^2}{a^2+b^2}$ 的圆。

$\it 4.2$ 极点极线、切线

【极点极线的概念】

• 平面上有二次曲线 $\Gamma:Ax^2+Cy^2+Dx+Ey+F=0$，则对于极点 $P(x_0, y_0)$，其关于曲线 $\Gamma$ 的极线为 $\ell_P:Ax_0x+Cy_0y+D\dfrac{x+x_0}{2}+E\dfrac{y+y_0}{2}+F=0$（即 $\begin{cases}x^2\to x_0x\\y^2\to y_0y\end{cases}$，$\begin{cases}x\to\dfrac{x+x_0}{2}\\y=\to\dfrac{y+y_0}{2}\end{cases}$）。（下文用 $\ell_M$ 表示 $M$ 点的极线）
  • 焦点和准线是一对特殊的极点极线。
• 几何定义：过 $P(x_0, y_0)$ 引圆锥曲线的两条割线，交于 $A, B, C, D$ 四点，$\ell_{AB}\cap\ell_{CD}=T$，则 $T\in\ell_P$（$A, B, C, D$ 四点顺序任意）。【常常作为出题的几何构造】

【极点极线的性质】

1. 对于圆锥曲线外一点 $P(x_0, y_0)$，过 $P$ 作椭圆的两条切线交椭圆于 $M, N$，则直线 $MN$ 就是点 $P$ 对应的极线。
2. 对于圆锥曲线上一点 $P(x_0, y_0)$，其极线为椭圆在 $P$ 处的切线。
3. 对于圆锥曲线内一点 $P(x_0, y_0)$，过 $P$ 引椭圆的一条割线交于 $A, B$，则椭圆在 $A, B$ 两点处的切线的交点构成的轨迹为 $\ell_P$。
4. 【配极原则】$Q\in\ell_P\lrArr P\in\ell_Q$。
5. 过 $P$ 作割线 $\ell_0$ 交圆锥曲线于 $AB$，$\ell_0\cap\ell_P=Q$，则 $\dfrac{PA}{PB}=\dfrac{QA}{QB}$（$P, Q$ 关于圆锥曲线调和共轭）。
   • $\dfrac{PA}{PB}=\dfrac{QA}{QB}$ 与 $\dfrac2{PQ}=\dfrac1{PA}+\dfrac1{PB}$ 等价。
   • 若 $A, B$ 在圆锥曲线的对称轴上，且 $A, B$ 关于圆锥曲线调和共轭，过 $B$ 作圆锥曲线的热议一条割线交于 $P, Q$，则 $\angle PAB=\angle QAB$。

【极点极线相关定值模型】

• 过椭圆 $\Gamma$ 外一点 $P(t, 0)$ 引割线 $\ell_{AB}$ 交于 $A, B$，$A'$ 为 $A$ 关于 $x$ 轴的对称点，$\ell_{A'B}\cap x=Q$，则 $\vec{OP}\cdot\vec{OQ}=a^2$。(双曲线，抛物线同理）
• $P$ 为椭圆外一点，$A, B$ 为椭圆左右顶点，$\ell_{PA}\cap\Gamma=C, \ell_{PB}\cap\Gamma=D$，$\ell_{CD}\cap x=Q$，则 $\vec{OP}\cdot\vec{OQ}=a^2$（双曲线同理）

$\it 4.3$ 定点模型

【定点模型理论】

• 自由度为 $1$ 的直线：要么过定点，要么定斜率，要么是其他少见形式（如椭圆切线）。
• 对于求直线过定点的题型，可以采取先猜后证的策略。
  1. 套用极点极线
  2. 常规模型
  3. 通过取特值猜出定点
  4. 考虑对称性

【常用定点模型】

1. 极点极线
   • 极点自由度为 $1$ 时极线自由度为 $1$，一般过定点。
   • 注意 $Q\in\ell_P\lrArr P\in\ell_Q$。
   • 判定极点极线：椭圆内接四边形 / 圆锥曲线上四点。
2. 过圆锥曲线上定点的直线斜率关系
   • 过圆锥曲线上定点 $P(x_0, y_0)$ 作其割线，交于 $A, B$，其中 $k_1=k_{PA}$ 和 $k_2=k_{PB}$ 满足一定关系（简单关系）。
     • $k_1\cdot k_2=m$，则 $\ell_{AB}$ 过定点 $(\dfrac{(a^2m+b^2)x_0}{a^2m-b^2}, -\dfrac{(a^2m+b^2)y_0}{a^2m-b^2})$。（椭圆）
     • $k_1+k_2=m$，则 $\ell_{AB}$ 过定点。
   • 当然有可能是斜率为定值的情况。

【证明方法体系】

1. 最优先：齐次化 - 平移
   • 平移变换：$\begin{cases}x=x'+a\\y=y'+b\end{cases}$
   • 由韦达定理获得 $k_1+k_2, k_1\cdot k_2$ 的值。
2. 先猜后证
   • 猜定点：
     1. 极点极线
     2. 常用模型判断
     3. 考虑多种特殊情况，来骗来偷袭！
     4. 考虑对称性
   • 方法 1：齐次平移。
   • 方法 2.1：直线过点；若定点在 $x$ 轴或其他直线上，代入根系关系，联立解出 $x$ 值。
   • 方法 2.2：三点共线；列斜率式 $k_1=k_2$。
   • 方法 3：一般证明法；写出直线的方程并证明其过定点。（很复杂，不推荐用）

$\it 4.4$ 定值模型

【中点弦定值相关（$-\dfrac{b^2}{a^2}$）】

• 形式：$k_1\cdot k_2=-\dfrac{b^2}{a^2}$
• 本质：仿射为圆
• 内容包括：
  1. 中点弦（对应圆中垂径定理）
  2. 切线（对应圆中切线垂直于半径）
  3. 斜率积为 $-\dfrac{b^2}{a^2}$ 的弦（对应圆周角定理）
• 见【仿射变换 & 斜率相关】

【垂直相关（斜率积为 $-1$）】

1. 设 $A, B$ 是椭圆上两个动点，满足 $k_{OA}\cdot k_{OB}=-1$，过原点向 $\ell_{AB}$ 作垂线交于 $H$，则：
   1. 点 $C$ 的轨迹方程为 $x^2+y^2=\dfrac{a^2b^2}{a^2+b^2}$，即 $|OC|=\dfrac{ab}{\sqrt{a^2+b^2}}$。
   2. $\dfrac1{|OA|^2}+\dfrac1{|OB|^2}=\dfrac1{a^2}+\dfrac1{b^2}$。
   3. 双曲线中 $b^2\to-b^2$ 即可。
2. （蒙日圆）由椭圆外一点向椭圆引两条切线切于 $A, B$，满足 $k_{PA}\cdot k_{PB}=-1$，点 $C$ 为弦 $AB$ 的中点，点 $Q$ 为椭圆上的另外一点，$\ell_{OQ}\cap\{x^2+y^2=a^2+b^2\}=E, F$，则：
   1. $|OP|=\sqrt{a^2+b^2}$。
   2. $O, C, P$ 三点共线，点 $C$ 轨迹为椭圆。
   3. $|QE|\cdot|QF|=|QF_1|\cdot|QF_2|$。
   4. 对于双曲线 $b^2\to-b^2$ 即可。

【斜率定值相关】

1. $k_1+k_2=0$（对称）
   • 过椭圆上一定点 $P$ 引两条弦 $PA, PB$，满足 $k_{PA}+k_{PB}=0$，则 $k_{OP}\cdot k_{AB}=\dfrac{b^2}{a^2}$
2. $k_1+k_2=2k_0$
   • 过椭圆内一点 $Q(t, 0)$ 作弦 $AB$，动点 $P\in\ell_Q$（极线），则 $k_{PA}+k_{PB}=2k_{PQ}$。（双曲线、抛物线同理）

【角度定值】（注：约定 $M$ 和 $\ell_M$ 为极点极线）

• 过椭圆上一点 $A$ 作切线交右准线与 $B$，右焦点为 $F$，则 $\angle AFB=90^\circ$。
• 过椭圆左焦点 $F$ 作弦 $AB$，$D$ 是椭圆右顶点，$\ell_F$ 为左准线，$\ell_{DA}\cap\ell_{F}=M, \ell_{DB}\cap\ell_F=N$，则 $\angle MFN=90^\circ$。
• 椭圆内 $Q(t, 0)$，$\ell_Q\cap x=P$，过 $Q$ 作弦 $AB$，则 $\angle APQ=\angle BPQ$。
• 过椭圆左焦点 $F$ 作两条弦 $AB, CD$，$\ell_{AC}\cap\ell_{BD}=P$，则有 $P\in\ell_F$。
• 过椭圆外一点 $P$ 引椭圆两条切线切于 $A, B$，则有 $\angle PF_1A=\angle PF_1B$，$\angle PF_2A=\angle PF_2B$。

$\it 4.5$ 焦点

【焦半径、焦点弦】

• 约定：取焦点弦与焦点所在坐标轴的锐夹角为 $\theta$。默认 $AB$ 为过椭圆某一焦点的焦点弦。$F_1, F_2$ 为左、右焦点。
• 【第二定义】$\dfrac{AF_1}{AH}=e$（左焦点对左准线，右焦点对右准线）

1. 椭圆焦半径：
   • $|AF_1|=a+ex_A$，$|AF_2|=a-ex_A$。
   • 角度式：长焦半径 $\rho_1=\dfrac{b^2}{a-c\cos\theta}$，短焦半径 $\rho_2=\dfrac{b^2}{a+c\cos\theta}$。
2. 双曲线焦半径（单支焦半径）：
   • $|AF_1|=-a-ex_A$，$|AF_2|=-a+ex_A$。
   • 角度式：同上。
3. 双曲线焦半径（异支焦半径）：
   • $|AF_1|=a+ex_A$，$|AF_2|=a-ex_A$。
4. 抛物线
   • $|AF|=x_A+\dfrac p2=\dfrac{p}{1\pm\cos\theta}$。

• 焦点弦推论
  • $\Large\color{Red}\star$ 若过圆锥曲线焦点 $F$ 的弦 $AB$ 有 $\dfrac{|AF|}{|BF|}=\dfrac nm$，其斜率为 $k$，则有 $e=\sqrt{k^2+1}|\dfrac{n-m}{n+m}|$。
  • 在圆锥曲线中，设过焦点 $F$ 切不与坐标轴垂直的直线交圆锥曲线于 $A, B$，其垂直平分线交焦点所在坐标轴于 $R$，则 $\dfrac{|FR|}{|AB|}=\dfrac e2$。
  • 椭圆或双曲线上任取一点 $P$，则以 $PF$ 为直径的圆与以原点为圆心、$a$ 为半径的圆相切（椭圆内切，双曲线外切）。

【焦点三角形、焦点角度相关】

• 焦点三角形基本做法：
  1. 单个焦点性质不好，通常两个焦点一起使用第一定义（不然无法利用条件）。
  2. 焦点三角形顶角处理方法。
  3. 熟悉经典构图，例如内接圆。
• 在椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 中，焦点为 $F_1, F_2$，$P$ 是椭圆上任意一点，$\angle F_1PF_2=\theta$，则 $S_{\Delta F_1PF_2}=b^2\cdot\tan\dfrac\theta2=b\sqrt{|PF_1|\cdot|PF_2|-b^2}$。
  • 双曲线：$S=\dfrac{b^2}{\tan\frac\theta2}=b\sqrt{|PF_1|\cdot|PF_2|-b^2}$。
  • 抛物线：$S=\dfrac{p^2}{2\sin\theta}$（$\theta$ 为过焦点直线的倾斜角）
• 椭圆中，左右焦点为 $F_1, F_2$，$P$ 为椭圆上任意一点 $\angle F_1PF_2=\theta$，则 $|PF_1|\cdot|PF_2|=\dfrac{b^2}{\cos^2\frac\theta2}=\dfrac{2b^2}{1+\cos\theta}$（双曲线中为 $\dfrac{2b^2}{1-\cos\theta}$）。若 $\angle PF_1F_2=\alpha, \angle PF_2F_1=\beta$，则 $e=\dfrac{\sin(\alpha+\beta)}{\sin\alpha+\sin\beta}$ 且 $\dfrac{a-c}{a+c}=\tan\dfrac\alpha2\tan\dfrac\beta2$。（双曲线中为 $e=\dfrac{\sin(\alpha+\beta)}{|\sin\alpha-\sin\beta|}$，$\dfrac{c-a}{c+a}=\tan\dfrac\alpha2\tan\dfrac\beta2$）
• 椭圆中，焦点在 $x$ 轴上，$\Delta F_1PF_2$ 是焦点三角形，$O_1$ 为其内心，延长 $PO_1$ 交 $x$ 轴于 $A$，则恒有 $\dfrac{|O_1A|}{|PO_1|}=e$，且 $O_1$ 的轨迹是以原椭圆两焦点为长轴顶点的新椭圆。其中 $O_1(ex_P, \dfrac{e}{e+1}y_P), A(e^2x_P, 0)$。
• 椭圆中，焦点三角形的旁切圆的轨迹为直线 $x=a$；双曲线的焦点三角形内切圆轨迹为 $x=a, x\in(-b, b)$；双曲线焦点三角形旁切圆轨迹为双曲线。
• $\color{Red}\Large\star$ 焦点三角形核心在于熟悉各种构图模式。

【光学性质】

• 设椭圆上一点 $P$，椭圆在 $P$ 处的切线为 $\ell_0$，$\ell_1\perp\ell_0$，则有 $\ell_1$ 平分 $\angle F_1PF_2$。（从椭圆一焦点发出的光线，经椭圆反射必经过另一个焦点）
• 双曲线同理
• 从抛物线焦点发出的光，经抛物线反射后与焦点所在坐标轴平行。

【焦点角度相关】

$\it 4.6$ 抛物线小专题

【阿基米德三角形（抛物线大模型）】

• 设抛物线 $\Gamma:y^2=2px$，抛物线上两点 $A(x_1, y_1), B(x_2, y_2)$，$Q$ 为弦 $AB$ 的中点，$\ell_1, \ell_2$ 分别为 $A, B$ 处抛物线的切线，$\ell_1\cap\ell_2=P$。
• 则：
  1. $\ell_{PQ}\parallel x$ 轴。
  2. $P(\dfrac{y_1y_2}{2p}, \dfrac{y_1+y_2}{2})$。
  3. 点 $C$ 为 $PQ$ 中点，则 $C\in\Gamma$，且 $C$ 点处的切线平行于 $\ell_{AB}$。
  4. $\Delta AFP\sim\Delta PFB$。
  5. （阿基米德三角形 $\Delta APB$）弦 $AB$ 与抛物线围成的图形面积为 $\dfrac23S_{\Delta APB}$。其中 $S_{\Delta APB}=\dfrac{|y_1-y_2|^3}{8p}$。
• 若弦 $AB$ 过焦点 $F$，记 $\ell_0$ 为准线，作 $AA'\perp\ell_0$ 交于 $A'$，$BB'\perp\ell_0$ 交于 $B'$，$Q'$ 为 $A'B'$ 中点。
  1. $\ell_{Q'A}, \ell_{Q'B}$ 切 $\Gamma$。$Q'F\perp AB, |Q'F|=\dfrac12|A'B'|$。$Q'A$ 平分 $\angle A'Q'F$，另一侧 $Q'B$ 同理。（初中几何某模型）
  2. $x_1x_2=\dfrac{p^2}{4}$，$y_1y_2=-p^2$。（坐标表示）
  3. $|AF|=x_A+\dfrac p2=\dfrac{p}{1-\cos\theta}, |BF|=x_B+\dfrac p2=\dfrac{p}{1+\cos\theta}$, $S_{\Delta AOB}=\dfrac{p^2}{2\sin\theta}$（$\theta$ 为弦 $AB$ 与焦点所在坐标轴的锐夹角）。
  4. 若 $\ell_0\cap x=E$，则 $k_{EA}+k_{EB}=0$。
  5. 以 $AF$ 为直径的圆与 $x$ 轴相切（记为 $\tt a$）；以 $BF$ 为直径的圆与 $x$ 轴相切（记为 $\tt b$）；以 $AB$ 为直径的圆与 $\ell_0$ 相切（记为 $\tt c$）。$\tt a$ 与 $\tt b$ 外切，$\tt a$ 和 $\tt b$ 分别与 $\tt c$ 内切。

$\it N$ 补丁

$\ell ink$

$\it N.1$ 圆锥曲线小题

【离心率】

1. 第一定义：双焦点构图，当解三角形做
2. 第二定义（较少）
3. 第三定义：处理斜率、垂直（包括中点弦）
4. 焦点相关：
   • 第一定义
   • $e=\sqrt{1+k^2}\cdot|\dfrac{n-m}{n+m}|$
5. 焦点三角形
   • 熟悉各种构图（如内心构图）
   • 常见公式：$S=b^2\tan\frac\theta2, r=(a-c)\tan\frac\theta2, h=\dfrac Sc, R=\dfrac{2c}{\sin\theta}$...

$\it N.2$ 运算形式补充

【运算形式】

1. 点坐标 + 设线联立（传统）
   • 将一切用点坐标以及斜率表示
   • 直线 $\cap$ 直线：$\dfrac{y-y_1}{x-x_1}=\dfrac{y-y_2}{x-x_2}$（列方程组然后向一定方向消元或配凑）
   • 直线 $\cap$ 圆锥曲线：线参 $y=kx+m$ 联立韦达
   • 垂直：斜率或向量
   • 长度：$|x_A-x_B|\cdot\sqrt{1+k^2}$
   • 面积
   • 角度
2. 点参三角式（参数方程）
   • $A(a\cos\alpha, b\sin\alpha)$
   • 弦公式 $\ell_{AB}$
   • 仿射变换赋予 $\alpha, \beta$ 几何意义
   • 使用三角恒等变换

$\it N.3$ 曲线系、四点共圆

形如 $\Gamma:ax^2+by^2+cxy+dx+ey+f=0$ 的曲线称为二次曲线。二次曲线包含椭圆、双曲线、抛物线（存在轴倾斜的情况）以及退化的两条直线。二次曲线的自由度是 $5$，即平面上 $5$ 个不共线的点可以确定唯一一条二次曲线。

曲线系常用于解决曲线与曲线交、直线与曲线交的情形，以及四点共圆、定点定值、几何证明。

如果两曲线交于四点，那么剩余自由度为 $1$，即可用 $\Gamma:\lambda C_1+\mu C_2=0$ 表示过这四点的所有曲线，然后使用待定系数法获得索所要的信息。

• 【二级结论】在椭圆（或双曲线、抛物线）$\Gamma$ 上存在不共线的四点 $A, B, C, D$，若这四点共圆，那么 $k_{AB}+k_{CD}=0$，其中 $A, B, C, D$ 四点的顺序可任意取。
  • 证明方法即设 $\ell_{AB}, \ell_{CD}$ 所代表的两条直线曲线系为 $T$，取过四点的新曲线 $E:\lambda\Gamma+\mu T=0$，其中新曲线 $E$ 为圆，其表达式 $E:ax^2+by^2+cxy+dx+ey+f=0$ 中 $a=b$ 且 $c=0$。带入直线后可得 $k_1+k_2=0$。
• 【tricks】对于单个直线与曲线相交可构造 $\Gamma+(\ell)^2=0$ 的形式。
• 大多证明方法是先表示出曲线系再比对系数，类似于抛物线点差法的使用过程。

$\it N.4$ 其他

表示方法：特殊表示方法（依据具体情况而定

极坐标系解圆锥曲线

! image

! image 双曲线

! image 抛物线

内准圆

求最值问题丁真放缩法

高庙上的曲线系

• $\Large\star$ 二次曲线 $C:Ax^2+By^2+Cxy+Dx+Ey+F=0$
• $C_1:F_1(x, y)=0, C_2:F_2(x, y)=0$
• 一般曲线系 $F(x, y)=\lambda_1F_1(x, y)+\lambda_2F_2(x, y)=0$

【临时例题】
$\ell ink$

---

非对称韦达

证明角度相等：相似三角形？