hot tea.

$\rm I$ 解析几何临时例题

Problem I 【非对称韦达】

【Description】已知椭圆 $\dfrac{x^2}4+y^2=1$，其长轴上两定点为 $A(-2, 0), B(2, 0)$。过 $P(1, 0)$ 作直线交椭圆于 $C, D$ 两点，证明：$k_{AD}\cdot k_{BC}$ 为定值。

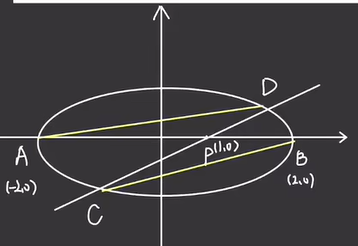
椭圆的第三定义：$k_{PA}\cdot k_{PB}=e^2-1$

貌似可以 参与运算？？

【Solution】

网上给了 n 中解法，自己发现可以先设 $\ell_{AD}, \ell_{BC}$ 的斜率为 $k_1, k_2$，然后用 $k_1, k_2$ 表示 $x_D, y_D, x_C, y_C$，由 $C, D, P$ 共线得 $\dfrac{y_D}{x_D-1}=\dfrac{y_C}{x_C-1}$，带入并因式分解得到 $(4k_1k_2+1)(3k_1-k_2)=0$。前者为椭圆的第三定义，那么取后者 $\dfrac{k_1}{k_2}=\dfrac13$。

Problem II 【齐次化-平移】

【Description】已知椭圆 $\dfrac{x^2}{6}+\dfrac{y^2}{3}=1$，其上有定点 $A(2, 1)$。过 $A$ 引两条互相垂直的直线 $\ell_{AM}, \ell_{AN}$ 交椭圆于 $M, N$。过 $A$ 作 $\ell_{AD}\perp \ell_{MN}$ 交 $\ell_{MN}$ 于 $D$。证明有定点 $Q$ 满足 $|DQ|$ 为定值。

【Solution】本题是齐次化 - 平移例题。

将坐标系原点平移至 $A$。设 $\ell_{MN}:mx+ny=0$。带入使用齐次化惯用手段得到 $m+n+\dfrac34=0$，解出过的定点是什么。

但是我们可以这样做：因为 $D$ 在一个圆上，而从 $D$ 出发已经有两条垂直的直线，那么就是说如果能在这两条直线上分别找两个定点，就可以构出斜边中线（可以证明这是充要的）。所以我们要做的就是找出 $\ell_{MN}$ 过哪一个定点 $P$，构出 $\Delta ADP$ 的斜边中线。

设其过的定点为 $P(x_0, y_0)$，并设 $\ell_{MN}:y=k(x-x_0)+y_0$。那么我们将 $\ell_{MN}$ 与椭圆联立。根据 $\ell_{AM}\perp\ell_{AN}$ 列式 $\dfrac{y_M-1}{x_M-2}\cdot\dfrac{y_N-1}{x_N-2}=-1$，发现该式对称，那么利用韦达定理算出 $x_M+x_N, x_Mx_N, y_M+y_N, y_My_N$ 关于主元 $k$ 和参数 $x_0, y_0$ 的式子，得到 $(9x_0^2-24x_0+12)k^2+(-18x_0y_0+24y_0+6x_0)k+9y_0^2-6y_0-3=0$。该式子可看成关于 $k$ 的二次方程，对于任意 $k$ 都有上式成立，则 $\begin{cases}9x_0^2-24x_0+12=0\\-18x_0y_0+24y_0+6x_0\\9y_0^2-6y_0-3\end{cases}$。解得 $P(1, 2)$（舍）或 $P(\dfrac23, -\dfrac13)$。故 $Q(\dfrac43, \dfrac13)$。

Problem III ?

【Description】椭圆 $\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$。椭圆上一点 $P$，过 $P$ 作椭圆的切线交直线 $x=4$ 与 $Q$。证明存在一定点 $D$，满足 $\ell_{PD}\perp\ell_{QD}$。

Problem IV ???

过椭圆外一点 $P$ 引椭圆的两条割线 $\ell_{AC}, \ell_{BD}$，且 $\ell_{OP}$ 过弦 $AB$ 的中点。求证：$\ell_{AB}\parallel\ell_{CD}$。

$\rm II$

• T1
  • $\cos(A+2B)+\cos A=\sin2B$
  • 求 $\min\{\dfrac{4a^2+5b^2}{c^2}\}$
• T2
  • 锐角 $\Delta ABC$，$\cos2B-\cos2A=4(\cos C-\cos^3C)$
  • 求 $\dfrac ab+\dfrac{b^2}{c^2}$ 取值范围
• T3
  • 锐角 $\Delta ABC$，角 $A, B, C$ 的对边依次为 $a, b, c$，满足 $2S_{\Delta ABC}=a^2-(b-c)^2$。求 $\dfrac{4b^2-12bc+17c^2}{4b^2-12bc+13c^2}$ 的取值范围。
  • 答案：$(\dfrac{281}{181}, 2]$

三角

• 化边或化角？
  • 看证什么？
    • 证角就化角，因为边证不了角
    • 如果考虑化边（转为 $a, b, c$ 的式子）那么就基本上就是用正弦、余弦等等。
• 代数化简
  • 原则：多倍化同倍，异名化同名，往待证的方向化简（如果没有直接的待证那么就当是要得到一个强力的角度关系）
  • 和差化积：一堆复杂的角的和差的同名三角函数加减，像 $\cos(A+2B)+\cos A=\sin 2B$
• 一个 trick：题目中给了角或边可以将值带入调节次数。

---

$\rm III\ \overrightarrow{\boldsymbol{Derivative}}$

$\it 50\ {Problems}$

Problem 1

Description

$f(x)=\ln x+\dfrac ax$

• 若不等式 $f(x)\ge\dfrac{2-e}{x}+a$ 对于 $x>0$ 恒成立，求 $a$ 范围。

Solution

必要性探路：取 $x=1$ 和 $x=e$，得到 $a\le 2$。

求导，$f'(x)=\dfrac 1x-\dfrac{e-2+a}{x^2}$，极值点 $x_0=e-2+a$。带入 $f(x_0)\ge0$ 求解即可。

Problem 2

Description

证明：对 $\forall a\in(0, 1)$，存在 $b>0$ 使得 $ae^b=a+b$，且 $2\ln a+b<0$。

Solution

画图，得到大致图像，确定方程有唯一合法解。

利用方程消元，$a=\dfrac{b}{e^b-1}$，$b$ 为原方程的零点，取值范围为 $(0, +\infin)$，问题转化为证明 $2\ln\dfrac{b}{e^b-1}+b<0$，即证 $\forall x>0, x^2e^x<(e^x-1)^2$。

写出函数 $g(x)=e^{2x}-(2+x^2)e^x+1$，$g'(x)=2e^{2x}-(x^2+2x+2)e^x=2e^x(e^x-\dfrac12x^2-x-1)$，经典不等式放缩得 $g'(x)>0$，带入端点原式得证。

Problem 3

Description

$f(x)=e^x\ln(x+1)$，证明：对 $\forall x, t\in (0, +\infin)$，有 $f(x+y)>f(x)+f(y)$。

Solution

思路：选取主元，证明不等式大于零（显然构造的函数是单调的）

令 $x<m$，构造 $g(x)=f(x+m)-f(x)$，则 $g(x)=e^x\cdot (e^m\cdot\ln(x+m+1)-\ln(x+1))$，即证 $(e^m\cdot \ln(x+m-1)-\ln(x+1))$，即政 $h(x)=e^m\cdot\ln(x+m-1)-\ln(x+1)$。

求导，$h'(x)=\dfrac{e^m}{x+m+1}-\dfrac{1}{x+1}$，易证 $h'(x)>0$。得证。

Problem 4

Description

同 Problem 3

Solution

Problem 5

Description

证明：$e^x\ln x-1+\dfrac{2e^{x-1}}{x}>0$

Solution

直接求导，发现零点没法弄，带入了几个点发现都取不到等去，于是考虑是不是没卡死的不等式，考虑放缩。

初步化简：即证 $\ln x+\dfrac{2}{ex}>e^{-x}$

画图，发现的确没卡死，那么考虑“隔离折线”。但是不好操作。

变一下，即证 $x\ln x>\dfrac{x}{e^x}-\dfrac{2}{e}$，隔离直线 $y=-\dfrac{1}{e}$。

一般在隔离直线的时候，函数的凹凸性得考虑一下。

---

放缩解法：

$\ln x-\dfrac{1}{e^x}+\dfrac{2}{ex}\quad\overset{e^x\ge ex}{\longrightarrow}\quad\ge\ln x-\dfrac{1}{ex}+\dfrac{2}{ex}=\ln x+\dfrac1{ex}>0$

$\Large\star$ Problem 6

Description

证明：对 $\forall x>1$ 有 $e^x-x^4+3x^3\ln x-x^2\ge 0$

Solution

$$\Leftrightarrow \dfrac{e^x}{x^3}-x+3\ln x-\dfrac1x\ge 0\\\Leftrightarrow e^{x-3\ln x}-(x-3\ln x)\ge \dfrac1x\\\Leftrightarrow e^t-t\ge \dfrac1x$$

$e^t-t\ge 1\ge \dfrac1x$

得证。

Problem 7

Description

证明：$a\le 1$ 时有 $xe^x-ax\ge \ln x+1$

Solution

$xe^x-ax\ge xe^x-x$

即证 $xe^x-x+\ln x-1\ge 0$

同构，$xe^x-\ln(xe^x)\ge 1\longrightarrow t-\ln t\ge 1$ 得证。

Problem 8

Description

证明：对 $\forall a\ge 1$ 有 $ae^x-x-a> x\ln x-\sin x$

Solution

放缩参数，只需证明 $a=1$ 时成立即可。

即证 $e^x-x-1-x\ln x>-\sin x$

设 $f(x)=e^x-1-x-x\ln x$，求导，$f'(x)=e^x-2-\ln x=0$，$f''(x)=e^x-\dfrac1x$。设 $f''(x)=0$ 的根为 $x_0$，则 $x_0e^{x_0}=1$，对 $f'(x_0)$ 的式子进行替换，$f'(x_0)=\dfrac1{x_0}-2+x_0\ge 0$，即 $f'(x)\ge 0$，$f(x)$ 单增。

隔离折线，只需证明 $x\in(0, \pi]$ 时 $e^x-x-1-x\ln x>0>-\sin x$，$x\in(\pi, +\infin)$ 时 $e^x-x-1-x\ln x>1>-\sin x$ 即可。

得证。

Problem 9

Description

证明：$\dfrac{1-\ln x}{e^x}+2x^2-\dfrac1x<2$ 在 $x\in(0, 1)$ 恒成立。

Solution

一眼 · 丁真，鉴定为：

$\dfrac{1-\ln x}{e^x}+2x^2-\dfrac1x<1-(\ln x+\dfrac1x)+2x^2$

$x\in(0, 1)\to\begin{cases} \ln x+\dfrac1x> 1\\ 2x^2< 2 \end{cases}$

得证。

Problem 16

Description

$f(x)=e^{x+1}+ax+a$

• 若 $x\ge 0$ 时，$f(x-1)+\ln(x+1)\ge 1$，求 $a$ 取值范围。

Solution

$g(x)=e^x+ax+\ln(x+1)-1$，$g'(x)=e^x+a+\dfrac{1}{x+1}$。

端点效应，带入 $x=0$，$g(0)=0$，则 $g'(0)\ge 0$，解得 $a\ge -2$。

若 $a\ge -2$，则 $g'(x)=e^x+a+\dfrac{1}{x+1}\ge 0$。带入 $x=0$ 得 $g(0)=0$。

答案为 $a\ge -2$。

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

$\sf link$

Problem 1

Description

$f(x)=(x-1)\ln x-a(x+1)$ 有两个零点 $x_1, x_2$。

1. 求 $a$ 的范围。（答案：$a>0$）
2. 证明 $\dfrac1{\ln x_1-a}+\dfrac1{\ln x_2-a}>0$

tag：极值点偏移、预处理变形

Solution

$\begin{cases} (x_1-1)\ln x_1=a(x_1+1)\\ (x_2-1)\ln x_2=a(x_2+1) \end{cases}\to\begin{cases} \ln x_1=a\cdot\dfrac{x_1+1}{x_1-1}\\ \ln x_2=a\cdot\dfrac{x_2+1}{x_2-1} \end{cases}$

$\dfrac1{\ln x_1-a}+\dfrac1{\ln x_2-a}=\dfrac{x_1-1}{2a}+\dfrac{x_2-1}{2a}>0\to x_1+x_2>2$

这样子代？

Problem 2

Description

$f(x)=ae^{x-1}-\ln x+\ln a$

• 若 $f(x)\ge 1$，求 $a$ 取值范围。

Solution

1. 同构。
   • $e^{x+\ln a-1}+x+\ln a-1\ge e^{\ln x}+\ln x$
2. 普通
   • $f'(x)=0$，解得 $x=x_0$，满足 $ae^{x-1}=\dfrac1x$
   • 然后把 $a$ 代成 $x_0$，发现刚好代完了。
   • 于是 $f(x_0)$ 与 $a$ 脱离了关系，直接求即可。
3. 还有。

Problem 3

Description

证明 $\sum\limits_{k=1}^n\dfrac1{\sqrt{k^2+k}}>\ln(n+1)$

Solution

首先常规数列不等式的套路，转化为证 $\dfrac{1}{\sqrt{x^2+x}}>\ln(x+1)-\ln x$

这怎么证？？？？？？？？？？？？？

瞎几把想ing

看一下均值不等式 $\sqrt{ab}<\dfrac{b-a}{\ln b-\ln a}$？

我去！做出来了！

$$\sqrt{x(x+1)}<\dfrac{(x+1)-x}{\ln(x+1)-\ln x}$$

还没看其他方法。

Problem 4

Description

$f(x)=x-\dfrac12\sin x-\dfrac m2\ln x+1$

• 若存在 $x_1, x_2\in(0, +\infin)$，且 $x_1\not=x_2$，$f(x_1)=f(x_2)$，证明：$x_1x_2<m^2$

Solution

这个东西取小于号和小于等于号有什么猫腻？

首先尝试极值点偏移，但是发现 $m$ 根本不是极值点！

那然后呢？不能用极值点的构造对称，那么要证明不等式成立，说明很可能并不是要取到等（卡死），而是能够放缩，而且正好三角函数基本是放缩。

于是只能模仿代数消元，先写关系式：
$\begin{cases}x_1-\dfrac12\sin x_1-\dfrac m2\ln x_1+1=T\\x_2-\dfrac12\sin x_2-\dfrac m2\ln x_2+1=T\end{cases}$

$x_2-x_1-\dfrac12(\sin x_2-\sin x_1)=\dfrac m2(\ln x_2-\ln x_1)$

运用三角函数放缩 $x>\sin x$ 得 $\dfrac m2(\ln x_2-\ln x_1)=x_2-x_1-\dfrac12(\sin x_2-\sin x_1)>\dfrac12(x_2-x_1)$，然后对数均值不等式悬而击之。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;

signed main() {

}

Problem 4

Description

$f(x)=ax-\ln x$，关于 $x$ 的方程 $f(x)=0$ 有两个不相等的实数根 $x_1, x_2$，其中 $x_1<x_2$。

1. 求实数 $a$ 的取值范围。
2. 设 $k$ 为常数，当 $a$ 变化时，若 $x_1^kx_2$ 有最小值 $e^e$，求常数 $k$ 的值。

Solution

一眼看过去，式子极其丑陋，那么考虑列出方程组作代换，凑 $x_1^k$ 出来。

$\begin{cases} kax_1=\ln x_1^k\\ ax_2=\ln x_2 \end{cases}$

于是 $a(kx_1+x_2)=\ln x_1^kx_2\ge e$

消去 $a$，得到 $a=\dfrac{\ln x_2-\ln x_1}{x_2-x_1}$

带入，齐次化，设 $t=\dfrac{x_2}{x_1}$，得到 $\ln t\cdot\dfrac{t+k}{t-1}\ge e$

那么问题转化为：已知定义域为 $(1, +\infin)$ 的函数 $f(t)=\ln t\cdot\dfrac{t+k}{t-1}$ 最小值为 $e$，求 $k$.

啊？？？

答案：$k=e^2-2e$

Problem 5

Description

$f(x)=e^x-x, g(x)=x-\ln x$

• 证明存在一条直线 $y=b$，使得该直线与 $f(x)$ 和 $g(x)$ 的图像共有三个交点，且交点的横坐标呈等差数列。

Solution

这不来一手同构？

画个图，发现 $y=b$ 必然交在 $f(x)$ 和 $g(x)$ 的交点处。

大概判断一下零点的大小关系，得 $x_1<0<x_2<1<x_3$

然后同构大显身手！$e^{x_1}-x_1=b, e^{x_2}-x_2=b, x_2-\ln x_2=b$

那么得 $e^{x_1}-\ln e^{x_1}=b$，所以 $e^{x_1}=x_2$ 或 $x_3$。由根的所在值域得 $e^{x_1}=x_2$。同理 $\ln x_3=x_2$。

即证 $e^{x_2}+\ln x_2=2x_2$。结合前面的式子易证。

Problem 6

Description

已知 $\begin{cases}a\ln x_1=2x_1-3\\a\ln x_2=2x_2-3\end{cases}$，求当 $x_2\over x_1$ 最小时 $a$ 的值。

Solution

先消元得到 $\dfrac{\ln x_1}{2x_1-3}=\dfrac{\ln x_2}{2x_2-3}$，然后设 $x_2=t\cdot x_1$，带入尝试各种操作看能不能分离，发现可以，完结。