速通统计与概率

无限期拖更中

统计与概率

概率

基本概念

$P(A)$ 表示事件 $A$ 发生的概率，$P(A)\in[0, 1]$。记 $P(AB)=P(A\cap B)$。

• $P(A\cup B)=P(A)+P(B)-P(AB)$
• $P(AB)=P(A)+P(B)-P(A\cup B)$（简单容斥）
• 若 $A\cup B=\varnothing$，则 $P(A\cup B)=P(A)+P(B)$
• $P(A-B)=P(A)-P(AB)$（集合减法：$P(A-B)=\{x|x\in A, x\not\in B\}$）
• 若 $B\subseteq A$，则有 $P(B)\le P(A)$，且 $P(A-B)=P(A)-P(B)$
• 对立事件：$P(\overline A)=1-P(A)$
• 分配率：$P\{(A\cup B)\cap C\}=P\{AC\cup BC\}$
• $P\{(AB)\cup C\}=P\{(A\cup C)\cap(B\cup C)\}$
• 对偶律：$P(\overline{A\cup B})=P(\overline A\cap\overline B), P(\overline{A\cap B})=P(\overline A\cup\overline B)$

---

条件概率：在某事件发生的前提下，某事件发生的概率

• 记 事件 $B$ 在 {事件 $A$ 发生 的前提下} 发生的概率为 $P(B|A)$
• $P(B|A)=\dfrac{P(AB)}{P(A)}$
• 乘法公式：若 $P(A)>0$ 则 $P(AB)=P(B|A)P(A)$
• $P(B\cup C|A)=P(B|A)+P(C|A)-P(BC|A)$（“$|$” 运算符优先级低）

---

独立事件：$P(AB)=P(A)P(B)$（不相互关联）$\Leftrightarrow P(B|A)=P(B) \Leftrightarrow P(B|A)=P(B|\overline A)$

全概率与贝叶斯公式

• 全概率公式：$P(A)=\sum\limits_{i=1}^nP(AB_i)=\sum\limits_{i=1}^nP(A|B_i)P(B_i)$（$A\subset\cup_{i=1}^nB_i$）
  • 当一个事件 $A$ 能够被一个 $B$ 事件完全分割（$\forall i, j\in[1, n], B_i\cap B_j=\varnothing$ 且 $\cup_{i=1}^nB_i=B$）
• 贝叶斯公式：$P(B_k|A)=\dfrac{P(B_kA)}{P(A)}=\dfrac{P(A|B_k)P(B_k)}{\sum\limits_{i=1}^nP(A|B_i)P(B_i)}$
  • 已知结果 $A$ 发生，判断是哪种情况。

离散型随机变量分布于分布函数

现有一随机变量 $X$，其可能取值为 $x_i, i=1, 2, ..., n$。

变量	$X$	$x_1$	$x_2$	...	$x_i$	...	$x_n$
取值概率	$P$	$p_1$	$p_2$	...	$p_i$	...	$p_n$

期望：$E(X)=\sum\limits_{i=1}^nx_ip_i$

方差：$D(X)=\sum\limits_{i=1}^n(x_i-E(X))^2\cdot p_i$

方差：$D(X)=E(X^2)-E^2(X)$

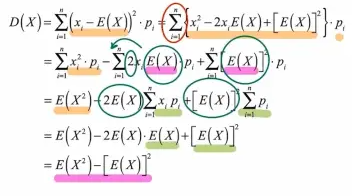
期望与方差的线性运算：

• $E(aX+b)=aE(X)+b$
• $D(aX+b)=a^2D(X)$

二项分布

在 $n$ 次，设每次的事件 $A$ 发生的概率为 $p$，用 $X$ 表示事件 $A$ 发生的次数，那么 $X$ 服从二项分布。记 $X\sim B(n, p)$。

• 显然，$P(X=k)=\dbinom{n}{k}p^k(1-p)^{n-k}$。
• $E(X)=np$
• $D(X)=np(1-p)$

超几何分布

$N$ 个球，$M$ 个黑球，剩下是白球，随机抽 $n$ 个。用 $X$ 表示 $n$ 个球中黑球的个数。

• $P(X=k)=\dfrac{\binom Mk\binom{N-M}{n-k}}{\binom Nk}$
• $E(X)=\dfrac MN\cdot n$
• $D(X)=\dfrac{nM(N-M)(N-n)}{N^2(N-1)}$

正态分布

若随机变量 $X$ 服从期望为 $\mu$，方差为 $\sigma^2$ 的正态分布，记为 $X\sim N(\mu, \sigma^2)$。

图像：

                  __-__
              __--     --__
        ___---             ---___
____----                         ----____

• $f(x)=\dfrac1{\sqrt{2\pi}\sigma}\cdot\exp[-\dfrac{(x-\mu)^2}{2\sigma^2}]$
• 对称轴：$x=\mu$
• 最大值：$f_{\max}=\dfrac1{\sqrt{2\pi}\sigma}\quad (x=\mu)$

ycycycy!

小学奥数 の 排列组合

$\rm I$ 基础

• 元素相邻：捆绑法（整体）
• 元素不相邻：插空法
• 充分利用组合意义 $\dbinom{n}{m}$ = 在 $n$ 个元素中选出 $m$ 个的方案数
• 对每个限制逐个突破，尽量消除他们之间的影响。
• 基础：隔板法及其变式
  • 当小球遇上盒子

$\rm II$ 进阶

• 容斥：当有很多个条件或者两个条件之间的羁绊实在拆不开的时候考虑容斥。

$\rm III$ 特殊题型

• 染色问题
  • 合理选取元素作为每一步分析
• 圆排列，错排
  • 圆排列 = 相应全排列 $\div\ n$
  • 错排公式：$D_n=(n-1)(D_{n-1}+D_{n-2}), D_1=0, D_2=1$

$\rm IV\ \textsf{gs}$

就是将整个求解过程分成若干步，每一步选取若干研究的元素，用组合式子表示答案，最终相乘（一条线的过程）

以上是线性的过程（只涉及乘法），还有分类讨论（加法）、容斥等。

可以看成一次消解若干自由度。

二项式定理及组合相关运算

$$(x+y)^n=\sum\limits_{i=0}^n\dbinom nix^iy^{n-i}\\T_i=\dbinom nix_iy^{n-i}$$

• $\dbinom nm = \dbinom n{n-m}$
• $\sum\limits_{i=0}^n\dbinom ni = \sum\limits_{i=0}^n\dbinom ni\cdot 1^i\cdot 1^{n-i}=(1+1)^n=2^n$