幻想几何 | 第 1 版

$\boldsymbol{3D\ Geometry}$

• by djs
• latest update: 2023.05.01

还有一堆石磊的《立体几何高级定理梳理》，貌似各种小结论挺多的。特殊图形结论待整理。

先整全再说，后面有需要再 AM 化。

构建思路

思维导图（方法 & 技巧） + $\textsf{General Solution}$

要把常用方法和 trick 分离出来。

• 过点作线的垂面
• 线面找交点、面面找交点
• 过点作面垂的一般方法
• 扩面的方法
• 割补观察图形的技巧
• 异面直线构造平行面（用于计算距离）

还有立体几何中的动静视角具体化（大概是一些轨迹）

$\rm I\ \textsf{General Solution}$

写一些暂时的见解。

【一些做题原则】

• 在点线面关系证明中，平移是线与面的等效替换的手段，故时刻可以考虑对线或面进行平移转化。
• 平面内两条直线代表这个面。
• 线面垂直是一一对应的强力关系，这也是法向量的原理。
  • 将不好处理的面转化为其对应的法向量。在空间向量建系的方法体系中，构造法向量和使用空间向量辅助计算两者是割裂开的，故前者可以考虑在纯几何环境中单独使用，处理一些不好处理的面。
• 角度信息不能实现跨面转化，故题目所给的角度信息应在平面内利用完全。
• 在动态的图形中，优先找定点分析。
• 图太难看了可以换个视角画图，也许有不一样的发现。
• 过于不好算的直接建系。

【立体几何与自由度分析】

• 标准：在立体几何中分析自由度时，务必注意要按照维度划分，一个维度算一个自由度。或者干脆将图形代数化分析，一个自由元算一个自由度。

【立体几何与平面几何】

• 不同之处
  • 升维给立体几何带来了不一样的几何体关系 - 线、面与之间的各种计算。
  • 同时直观分析（幻想）的作用减弱了。
  • 不能对图形进行解析。
• 不变之处
  • 各种平面几何的 trick 到了三维世界中仍然发挥着作用，例如将军饮马、胡不归等等。
  • 只不过换了一套新的模子和定理。

【幻想的实质】

• 常说的幻想，就是对图形位置关系和动态对象的直观想象与分析。
• 规整的图形、垂直条件有利于幻想。
• 幻想能够发现一些隐藏的位置关系条件，从直观的层面上把握题目。
• 幻想要结合自由度理论分析，可以将剩余自由度具体化为轨迹。“点动成线，线动成面”。
• 幻想用得好会带来很大便利，但不能过于依赖。

$\rm II\ \textsf{General Tricks}$

【过点作线的垂面】

• 转化为过一个点找两条垂直于目标直线的直线。
• 然后可以直接幻想，或者借助已知的面，通过三垂线定理作垂。
• 作出来的两条直线构成的面就是垂面。

【线面找交点、面面找交线】

• 线面交点是不好找的，除非是直接与平面内的直线相交，否则一般转化为面面交线的问题。
• 面面找交线转化为找到两个同时处在两个面上的点，然后连接得到交线。
• 注意找不到这样的点可以考虑扩面。
• 扩面延长直线的原则是向面面交线延长，作出交点。

【过点作面的垂的方法】

• 核心就是找一个垂面，然后作交线的垂。
• 比如说在面中找到一组平行线，分别过点作两条线的垂线，得到两个垂足。连接两个垂足，得到新的直线。过原来的点在这条直线作垂即可得到点在面上的投影。

【扩面的方法】

• 所谓扩面，就是对一些特定线段锁定的面进行扩展，作出更多的交点或交线，以便更好地进行性质分析。
• 其一：延长直线扩展平面，然后连接平面内的点获得交线（一般方法）
• 其二：平移直线扩展平面（在对面有平行面的时候使用，例如正方体中）
• 其三：利用四点共面定理暴算（通常为难以确定的复杂位置）

【图形割补的观察技巧】

• 在对复杂立体图形进行割补时，我们对割补的截面重点分析，这样可以辅助对图形的幻想，避免割漏的情况。

【异面直线构造平行平面】

• 将两条直线彼此向对方平移至相交。
• 此时就可以将这两条直线之间的距离转化为新构出来的两个平面的距离。

【将立体几何转化为平面几何】

• 不好幻想时，可以先分析平面上的对象，辅助分析空间的图形。
• 作投影（例：三垂线）
• 作轴截面
• ...

$\rm III$ 体积问题

• 唯一能直接处理的体积：棱柱、棱锥（公式）
  • 以及常用几何变换
• 割补
• 补形
• 其他定理

$\it 3.1$ 公式

• 棱柱公式：$V=S\cdot h$
• 棱锥公式：$V=S\cdot h\cdot\dfrac13$
  • 棱锥即平面上一个图形和平面外一点形成的空间几何体。
• 台体：$V=\dfrac13(S_1+\sqrt{S_1S_2}+S_2)\cdot h$
• 球
  • 体积：$V=\dfrac43\pi r^3$
  • 表面积：$S=4\pi r^2$

一个奇怪的体积求法：“铅锤面”（类比平面几何的铅锤线法）。

【棱锥平移顶点】

• 可以将顶点在过该点且平行于底面的平面中移动，从而实现对体积的转化。

【底面积转化】

• 在同高的情况下，棱锥的体积比等于底面积的比。所以可以对所求的体积实现这个转化。

【辛普森公式】

• 适用于拟柱体（两个平行平面去若干点然后连边）
• $V=\dfrac16h(S_0+S_2+4S_1)$，其中 $S_1$ 为各棱中点构成的图形的面积。

$\it 3.2$ 割补

割补对空间幻想能力的要求比较高，目前准确率较高的观察方法是看截面，也就是通过观察和记录割面来想象要处理的图形的模样。这样通过割补割出来的截面就可以确定是否割补正确。

割补方向：转化为能直接处理的图形（公式法）。

祖暅原理：对于夹在两个平行平面之间的两个几何体，当被平行于这两个平面的任意平面所截时，如果截面的面积总相等，那么这两个几何体的体积必然相等。（微积分衍生结论）

$\it 3.3$ 补形

• 结论：任意一四面体都内接于唯一的平行六面体中，且体积为其 $\dfrac13$。
• 若四面体的一组对棱相等，那么对应的平行六面体的两个对面就变为长方形。如果四面体三组对棱都相等，那么该四面体内接于长方体中。
• 凡是看到对棱相关条件就考虑平行六面体补形。（或者一些规整的图形，例如正方体，长方体）

$\it 3.4$ 其他定理

• 三棱锥体积比定理（见后文）

$\rm IV$ 线面位置关系

$\it 4.1$ 平行

【判定定理】

• 线面：$a\not\subset\alpha, b\subset\alpha, a\parallel b \to a\parallel\alpha$
• 面面：$a\parallel\alpha, b\parallel\alpha, a\subset\beta, b\subset\beta \to \alpha\parallel\beta$（两条相交直线代表一个平面）
• （法向量）$a\perp b, b\perp\alpha \to a\parallel\alpha$

【处理方法】
处理平行的方法，一言以蔽之：平移。

• 将线平移至目标平面上：表现为在平面内找一条与待证直线平行的直线。
• 将平面平移到目标直线上：表现为将待证直线装入与目标平面平行的平面，或者构造平行平面。
  • 也可以考虑将面转化为法向量。

注意各种初中几何中中位线的常用构造（例如 $\rm T$ 形构造）仍然较为常用，本质仍是线段的平移转化。在遇到中点条件时考虑使用。

$\it 4.2$ 垂直

【判定定理】

• 线面垂直：证明线与面内两条相交直线垂直 $(a\subset\alpha, b\subset\alpha, a\cap b=A,l\perp a, l\perp b \to l\perp\alpha$）。
• 面面垂直：证明一个平面内的一条直线垂直于另一个平面（主要考虑转线面垂直）。
  • 或者考虑作一个面的法向量然后证平行。

【一般方法体系】

• 异面直线垂直
  • 三垂线定理
  • 转化为线面垂直（将一条直线装入平面）
  • 平移等等（看成异面直线夹角 $90^\circ$）
• 线面垂直
  • 转化为线和面中两条直线垂直。
  • （很少情况下）转化为面面垂直。
• 面面垂直
  • 在一个平面内作交线的垂，转化为线面垂直。
  • 三余弦等等（看成二面角 $90^\circ$）
• 建半个系，作面的法线转化。

【三垂线定理】

• 用于证明异面直线垂直和作二面角。
• 内容：$l$ 为 $a$ 在平面 $\alpha$ 上的射影，$b\subset\alpha$ 且 $l\perp b$，则有 $a\perp b$。
• 可以看做是构造面面垂直。
• 作线的垂面可以转化为作两条垂线锁定平面。
• 其逆定理成立。

$\it 4.3$ 夹角

【异面直线夹角】

• 相对通法：平移。
  • 综合利用其他条件，例如平移到一起后使用三余弦定理求解。
• 对角线向量定理：见后文。
• 向量夹角公式（或者直接建系）

【线面角基本方法】

• 一般的方法为用定义构图（无需真正将垂做出来，只用求距离），关键是求点到面的距离（转化为求点到面的距离）。
• 在最值问题中套用最小角定理。
• 先假设作了一个垂，然后用三余弦定理暴算确定垂的位置。
• 建半个系，作面的法线转化。
• 使用线面角万能公式。

【二面角】

• 用三垂线定理法作出二面角求解
  • 先作点到面的垂，然后作垂足到交线的垂。
• 面积射影定理：用于有点到面的射影时：见后文。（要求点的射影好作）
• 二面角 の 最终最强定理 - 三余弦定理：见后文。
• 建半个系，作面的法线转化。
• 建系法向量。
• 二面角之间可以加减。

【最大角定理、最小角定理】

• 线面角是线线角的最小角。
• 二面角是线线交的最大角。
• 主要是做一些最值的题目的时候起到充要替换的作用。

【四直角四面体模型求各种角】

• 见后文模型部分。

$\rm V$ 距离计算

• 点点距离
  1. 找第三个点解三角形。
  2. 将线段所在向量分解为基向量，平方数量积。
  3. 建系
• 点面距离
  1. 最常用：三棱锥体积法
  2. 将点在对应的平行的面内移动，转化为另一个点到原面的距离。
  3. 建系使用法向量计算公式。
  4. 点面距离也可以用二面角求：$d=h\sin\theta$（等等其他的求法）
• 异面直线的距离
  1. 两条直线向对方平移（前文有）造面，转化为面面距离（点面距离）。
  2. 作公垂线计算。（见 $\rm II$）
  3. 写出两点距离的代数表达式，主元求最值。
  4. 新模型
     • 若面 $\alpha\perp\beta$，$\alpha\cap\beta=\ell_0$，在 $\ell_0$ 上有两点 $A, B$，$A\in\ell_1, \ell_1\in\alpha$; $B\in\ell_2, \ell_2\in\beta$。$\langle\ell_0, \ell_1\rangle=\theta_1, \langle\ell_0, \ell_2\rangle=\theta_2$，则 $\ell_1, \ell_2$ 之间的距离为 $d=|AB|\cdot(1+\cot^2\theta_1+\cot^2\theta_2)^{-\frac12}$。

$\rm VI$ 高级定理及使用方法、结论汇总

$\it 6.1$ 高级定理

• 三余弦定理（最高频！）
  • 内容：任意从 $P$ 引出三条射线 $PA,PB,PC$，记 $\left<PA,PB\right>=\alpha,\left<PA,PC\right>=\beta,\left<PB,PC\right>=\gamma$，二面角 $B-PA-C$ 为 $\theta$，则满足 $\cos\gamma=\cos\alpha\cos\beta+\sin\alpha\sin\beta\cos\theta$。
  • 图形观察
    1. $P-ABC$ 的爪形结构
    2. 对应的二面角
  • 特殊情况：$\theta=\dfrac\pi2$
    • 也就是二面角为垂面的情况，此时有 $\cos\gamma=\cos\alpha\cos\beta$
  • 用法：可以求二面角，更多的是已知二面角（或垂面）用来推导一些异面的角度关系。
• 四点共面定理
  • 若空间内 $P,A,B,C$ 四点共面，且 $A,B,C$ 三点不共线，则对于任意平面外一点 $O$，存在实数 $x,y,z$ 满足 $\vec{OP}=x\vec{OA}+y\vec{OB}+z\vec{OC}$，且 $x+y+z=1$。反之亦然。（即其中一个向量分解为另外三个向量的系数和为 $1$）
• 对角线向量定理
  • $\vec{AC}\cdot\vec{BD}=\dfrac12[(|AD|^2+|BC|^2)-(|AB|^2+|CD|^2)]$
  • 将四面体对棱向量的数量积用四条边表示，可以用于求四面体对棱的夹角。
• 面积射影定理
  • 设锐二面角 $\alpha-l-\beta$ 为 $\theta$，在一个半平面 $\alpha$ 中有一个面积为 $S$ 的封闭图形，该图形在另一个平面 $\beta$ 上的射影的面积为 $S'$，则 $\cos\theta=\dfrac{S'}{S}$。
  • 在求二面角时如果各点的射影都很好作那么可以考虑使用此法。此法的优点是不需要作出两面的交线。
  • 在某些截面面积最值（例如二面角固定）中可以使用。
• 三棱锥体积比定理
  • 在一个三棱锥 $P-ABC$ 中，$D$ 在 $PA$ 上，$E$ 在 $PB$ 上，$F$ 在 $PC$ 上，则有：
  • $\dfrac{V_{P-DEF}}{V_{P-ABC}}=\dfrac{|PD|\cdot |PE|\cdot |PF|}{|PA|\cdot |PB|\cdot |PC|}$
• 外接球半径万能公式
  • 已知二面角 $P-AB-C$，其中 $\Delta PAB$ 的外心为 $O_1$，$\Delta ABC$ 的外心为 $O_2$，二面角为 $\theta$。过 $O_1$ 作 $AB$ 的垂，过 $O_2$ 作 $AB$ 的垂同时交于一点 $D$，那么四面体 $P-ABC$ 的外接球半径 $R$ 可表示为：
  • $R=\sqrt{\dfrac{|O_1D|^2+|O_2D|^2-2\cdot |O_1D|\cdot |O_2D|\cdot\cos\theta}{\sin^2\theta}+\dfrac{|AB|^2}{4}}$
• 三正弦定理
  • 
• 线面角万能公式
  • 记 $AB$ 与面 $BCD$ 的夹角为 $\varphi$，其中 $\varphi\in[0, \dfrac\pi2]$；
  • $\angle ABD=\theta_1, \angle ABC=\theta_2, \angle DBC=\theta$
  • 则有：$\cos^2\varphi=\dfrac{\cos^2\theta_1+\cos^2\theta_2-2\cos\theta_1\cos\theta_2\cos\theta}{\sin^2\theta}$

$\it 6.2$ 结论汇总

【1】补形基础结论

• 任意一四面体都内接于唯一的平行六面体中，各组对棱分别是平行六面体对面的对角线，且体积为对应平行六面体的 $\dfrac13$。
• 若某组对棱相等，那么对应平行六面体中的对面转化为矩形（三组对棱分别相等，原四面体内接于长方体中）。

【2】最大角与最小角定理

• 最小角定理：线面角是线线角的最小角
• 最大角定理：二面角是线面角的最大角

【3】在任意一四面体中，两组对棱垂直，那么第三组对棱一定垂直。且任意一定点在其对面上的射影必为其垂心。

【4】三棱锥定点投影相关结论

三棱锥顶点 $P$ 投影	常见充要条件
$P$ 为外心	$PA=PB=PC$ 或三条侧棱与底面的线面角相等
$P$ 为内心	三个侧面与底面的二面角相等 或 从 $P$ 出发的三个侧面的高相等
$P$ 为垂心	一个顶点的投影是垂心，等价于四个点的投影都是垂心，等价于两组对棱垂直，等价于三组对棱垂直
$P$ 的投影在 $\angle BAC$ 的平分线上	常见充要条件：$\angle PAB = \angle PAC$
投影在某条线段上	等价于面面垂直

【5】在坐标系中，重心坐标为三点坐标加起来除以 $3$。

【6】坐标轴的性质

• 一条直线 $OP$ 与三个坐标轴的夹角为 $\alpha, \beta\, \gamma$，则有 $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$

$\it 6.3$ 四直角四面体模型（鳖臑）

• 来自《拉档提分》。

基本模型

四直角四面体模型是一个四个面都是直角三角形的四面体，在这个四面体中有诸多结论，可以求解各种角度相关问题（作为上面一堆结论的补充）。

（可能本质上就是把一堆定理揉在一起了）

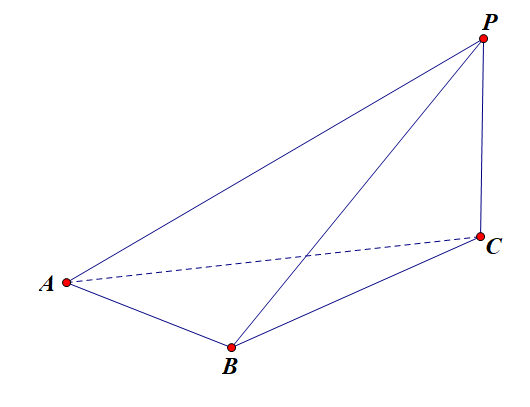
• 设 $\beta=\left<PA, ABC\right>, \delta=\left<AC, PAB\right>, \alpha=\left<AB, AC\right>, \theta=\left<AP, AB\right>, \varphi=\left<PAB, ABC\right>, \psi=\left<PAB, APC\right>$
• 结论如下：
  • $\cos\theta=\cos\alpha\cos\beta$
  • $\sin\varphi=\dfrac{\sin\beta}{\sin\theta}$
  • $\sin\psi=\dfrac{\sin\alpha}{\sin\theta}$
  • $\sin\delta=\sin\alpha\sin\varphi$
• 理解方式：可以理解为用三条互相垂直的线假装建立一个“坐标系”（图中的 $PC, CB, BA$），然后利用这些结论进行“解析”。

拓展模型

此拓展模型只需要两个互相垂直的面即可成立，相对更好用。

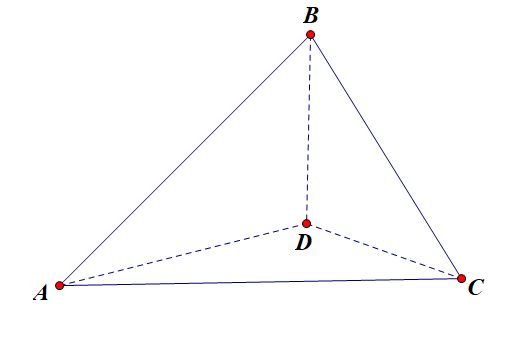
• $\angle BAD=\beta, \angle CAD=\alpha, \angle BAC=\theta, B-AC-D=\varphi, C-AB-D=\psi, \left<AD, BAC\right>$
• 条件：$B-AD-C=\dfrac\pi2$
• 结论：
  • $\cos\theta=\cos\alpha\cos\beta$
  • $\sin\varphi=\dfrac{\sin\beta}{\sin\theta}$
  • $\sin\psi=\dfrac{\sin\alpha}{\sin\theta}$
  • $\sin\delta=\sin\alpha\sin\varphi$

$\rm VII$ 球相关

$\it 7.1$ 外接球

• 外接球球心作图要点：过两个外心作面的垂涎交于一点（进一步可以计算二面角）。
• 个别情况可以直接设出球心的坐标然后暴算。
• 注意外接球公式。（见高级定理）

$\it 7.2$ 内接球

• 内接球半径求法
  • 棱柱、棱锥：$\dfrac{3\times V}{S}$
  • 圆锥：直接作图计算。
• 某些比较对称的图形的内切球可以直接作图计算。

$\it 7.3$ 棱切球

• 对于规整的图形，作轴截面
• 更通的方法是（对于四面体）找一个面的内心，然后过之作面的垂线，棱切球球心在直线上。

$\rm VIII$ 各种最值问题、轨迹

• 在动静视角中，一切自由度都可以具体化为轨迹。
• 本节会偏初中几何一些。

$\it 8.1$ 轨迹

• 动点问题的充要替换：点的轨迹看成线，线的轨迹看成面。
• 自由度为 $1$ 的直线构成平面。
  • 动线 $\parallel$ 定面
  • 动线 $\perp$ 定线
  • 到两个定点距离相等的点的轨迹
  • 到两个定直线夹角相等的直线的轨迹
• 对定直线张角为 $\dfrac\pi2$ 的点构成球面。
• 与定直线夹角成一定值的直线构成圆锥的侧面。

$\it 8.2$ 最值与几何 の $\textsf{trick}$

• 结合动静视角进行分析。
• 阿氏圆、阿氏球
  • 作相似即可。
• 多线段求最值
  • 展开图降维打击
  • 将军饮马类对称构图（注意对称一定要是定点）
  • 胡不归类带系数问题：找对应三角函数构图
• 自由度较高时记得使用主元法
• 面积最值：
  • 可以考虑在已知二面角的情况下，利用面积射影定理将带求面积转化为一平面上的图形。
• 找轨迹
  • 原则是找限制关系（平面、球）降低自由度（一般降到 $1$）
  • 球 $\cap$ 球 $=$ 圆
  • 球 $\cap$ 平面 $=$ 圆
  • 平面 $\cap$ 平面 $=$ 线

$\rm IX$ 杂项

$\it 9.1$ 特殊图形的结论 - 正四面体

$\begin{matrix}S=\dfrac{\sqrt 3}4a^2 & h=\dfrac{\sqrt 6}3a & V=\dfrac{\sqrt 2}{12}a^3 & R_{外接球}=\dfrac{\sqrt 6}{4}a & R_{内接球}=\dfrac{\sqrt 6}{12}a\end{matrix}$

$\it 9.2$ 特殊图形的结论 - 正方体、长方体

$\it 9.3$ 特殊图形的结论 - 墙角

真 · 杂项

计数问题：通用想法轨迹法。

$\rm X$ 空间向量建系暴算

$\it 10.1$ 相关 $\textsf{General Solution}$

待整理。

空间向量建系能干什么？首先他的本质是三维直角坐标系的不完全解析他不能解析面，但是将面转化为法向量，从而用向量表示一些几何的量。

感觉空间向量他有一定的万能性，能够作为某些几何很难解的题的最终杀招，但是也有本身的局限性。空间向量对付方正的图形效率较高，比如正方体。而纯几何法面对一些无法用代数表示的东西会有优势。

$\it 10.2$ 计算法则

• $\vec m=(x_m, y_m, z_m)$
• $\vec n=(x_n, y_n, z_n)$
• $|\vec m|=\sqrt{x_m^2+y_m^2+z_m^2}$
• $\vec m+\vec n=(x_m+x_n, y_m+y_n, z_m+z_n)$
• $\vec m\cdot\vec n=x_mx_n+y_my_n+z_mz_n$
• $\vec m$ 与 $\vec n$ 共线（平行） $\leftrightarrow$ $\vec m=\lambda\vec n$
• $\vec m$ 与 $\vec n$ 垂直 $\leftrightarrow$ $\vec m\cdot\vec n=0$
• $\vec m$ 与 $\vec n$ 的夹角：$\cos\left<m, n\right>=\dfrac{\vec m\cdot\vec n}{|\vec m|\cdot|\vec n|}=\dfrac{x_mx_n+y_my_n+z_mz_n}{\sqrt{x_m^2+y_m^2+z_m^2}\cdot\sqrt{x_n^2+y_n^2+z_n^2}}$

$\it 10.3$ 空间向量核心方法

将线替换为向量，平面替换为唯一对应的法向量，用空间向量运算法则辅助计算。

计算法向量的方法：设参，用两条平面内直线垂直联立方程。注意解出来的法向量的自由度为 $1$，可以自行给一个元赋值。

• 在题目中使用坐标来解决立体几何的问题时没有面的概念，有关面的题目将面转化成该面的法向量，法向量即与该面垂直的向量。
• 关于垂直：分为线线垂直（所求线段向量点乘等于零），线面垂直（所求线段向量与所求面的法向量平行），面面垂直（所求两面的法向量点乘等于零）。
• 关于平行：分为线线平行（所求线段向量平行），线面平行（所求线段向量与所求面的法向量点乘等于零），面面平行（所求两面的法向量平行）。
• 关于夹角：分为线线相交所成夹角（利用 $\cos\alpha = \dfrac{\vec a\cdot\vec b}{|\vec a||\vec b|}$ 注：线线相交所成夹角为锐角或直角），线面相交所成夹角（利用所求面的法向量与所求线段向量的夹角），面面相交所成夹角（利用所求两面的法向量的夹角 注：注意判断此时 $\cos$ 的正负）。

【线面关系】（$\vec m, \vec n$ 为 $\alpha, \beta$ 的法向量）

	线线（$\vec x, \vec y$）	线面（$\vec x, \alpha$）	面面（$\alpha, \beta$）
垂直	$\vec x\cdot\vec y = 0$	$\vec x\parallel\vec m$	$\vec m\cdot\vec n = 0$
平行	$\vec x = \lambda\vec y$	$\vec x\cdot\vec y = 0$	$\vec m = \lambda\vec n$
夹角	$\cos\theta = |\dfrac{\vec x\cdot\vec y}{|\vec x||\vec y|}|$	$\sin\theta = \cos(\frac\pi2 - \theta) = |\dfrac{\vec x\cdot\vec m}{|\vec x||\vec m|}|$	$\cos(\pi - \theta) = \dfrac{\vec m\cdot\vec n}{|\vec m||\vec n|}$（注意法向量向内作）

$\it 10.4$ 常用向量公式

叉积计算法向量

$\vec a=(x_1,y_1,z_1),\vec b=(x_2,y_2,z_2)$，求 $\vec a, \vec b$ 构成的平面的法向量。

$\vec m = \vec a\times\vec b$

口诀：

1. 向量横着写两遍

$$\begin{matrix} x_1 & y_1 & z_1 & x_1 & y_1 & z_1\\ x_2 & y_2 & z_2 & x_2 & y_2 & z_2 \end{matrix}$$

2. 掐头去尾留中间

$$\begin{matrix} \not x_1 & y_1 & z_1 & x_1 & y_1 & \not z_1\\ \not x_2 & y_2 & z_2 & x_2 & y_2 & \not z_2 \end{matrix} \to \begin{matrix} y_1 & z_1 & x_1 & y_1\\ y_2 & z_2 & x_2 & y_2 \end{matrix}$$

3. 交叉相乘再相减

$$\begin{matrix} y_1 & & z_1 & & x_1 & & y_1\\ & \times & & \times & & \times & \\ y_2 & & z_2 & & x_2 & & y_2 \end{matrix} \to \begin{matrix} y_1z_2-z_1y_2 & z_1x_2-x_1z_2 & x_1y_2-y_1x_2 \end{matrix}$$

最终得到平面的一个法向量（叉乘结果） $\vec m=(y_1z_2-z_1y_2, z_1x_2-x_1z_2, x_1y_2-y_1x_2)$，其模长为 $|\vec m|=|\vec a||\vec b|\sin\theta$

注意 $\vec a\times\vec b$ 和 $\vec b\times\vec a$ 的结果是两个相反的向量。建议搜索：右手定则。

点到面的距离算法

求空间内一点 $A$ 到平面 $\alpha$ 的距离。

• 先找一点 $B\subset\alpha$，算出 $\alpha$ 的单位法向量 $\vec m$（$\vec m$ 向 $A$ 的方向作），那么所求距离 $d=\vec{BA}\cdot\vec m$。
• 或者随便乘上一个法向量，然后除以这个法向量的长度。

点到线的距离算法

求空间内一点 $A$ 到直线 $\mathit l$ 的距离。

• 先找一点 $B\subset l$，算出 $l$ 往垂足方向上的方向向量 $\vec m$（或者随便一个该方向上的向量除以其模长），那么就可以得到 $A$ 到垂足的距离。最后使用勾股定理求解。

异面直线距离

求两条异面直线 $\ell_1, \ell_2$ 之间的距离

• 设平面 $\alpha$ 为 $\ell_1, \ell_2$ 所共的平面，其法向量为 $\vec m$。选取任意的 $A\in\ell_1, B\in\ell_2$，记 $\vec{AB}=\vec p$，则 $d=\dfrac{\vec p\cdot\vec m}{|\vec m|}$。
• 注：若需求 $A, B\in\ell_1, C, D\in\ell_2$ 的 $V_{A-BCD}$，则以 $\vec{AB}, \vec{CD}, \vec m$（其中 $\vec m$ 为法向量）为方向将 $A-BCD$ 放进平行六面体中（补形），利用直线间距离 $d$ 和相应面积求解。